Download LHC Physics Goals

LHC Physics Goals
Paris Sphicas
CERN/Univ. of Athens
LECC 2002
Colmar, September 2002

Paris Sphicas
Outline
 The Standard Model of Particle Physics
 Symmetry Breaking and the Higgs boson
 Higgs search at the LHC
 Supersymmetry
 TeV-scale gravity; large extra dimensions (?)
 Summary/Conclusion
LHC Physics Goals
1
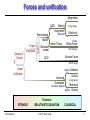
Forces and unification
Magnetism
QED
Electro
magnetism
M axwell
Quantum
Gravity
Grand
Unification
SUSY?
Electroweak
Model
Standard
model
Electricity
Fermi
Weak Theory
Weak Force
Short range
Nuclear Force
QCD
?
Short range
Super
Unification
Kepler Celestial
Gravity
Universal
Gravitation
Long range
Einstein, Newton
STRINGS?
Paris Sphicas
Long range
Theories:
RELATIVISTIC/QUANTUM
LHC Physics Goals
Terrestrial
Galilei Gravity
CLASSICAL
2
Relativity means fields

Action can only travel at speed vc.
 Communication between disparate space-time points
as long as within “light-cone”
t
x


Thus, operators (that finally yield observables) are a
function of x,t; i.e. fields
Same argument holds with measuring position of a
particle (position operator)
Paris Sphicas
LHC Physics Goals
3
Quantum Mechanics

We measure probability of occurrence
 Discrete absorption and emission


Bohr model: explain why atom is stable
“equations of motion” involve complex (instead of real)
quantities: y=a+ib; interference: we measure |y|2

when two things y1 and y2 “happen”, final observable is NOT
|y1|2+ |y2|2. It is |y1+ y2|2= |y1|2+ |y2|2+2Re{y1*y2}
Electron density waves seen to
be breaking around two atomsized defects on the surface of a
copper crystal
Paris Sphicas
LHC Physics Goals
4
Quantum Field Theory
Quantum mechanics + relativity  quantum fields
 Transmission by quantum of the field


i.e. by the particle of the field
Electroweak
Electromagnetic
e
Charged

+
Weak
q
-
e
q
e+
e+
e
u
W
d
e-
e
-
e
Range , relative strength =10-2
Paris Sphicas
e
e
Neutral
u
d
q
e+
+
e
Zo
-
e
e+
e+
e-
e-
Range ~10-18 m, relative strength ~10-14
LHC Physics Goals
q'
g
q
eq
Zo
W

-
-
Strong
q
q'
g
g
q'
q'
g
g
g
16
g
g
g
g
g
Range ~ 10-15 m, relative strength = 1
5
Particles and Forces
But then why is there more than one force in nature?

Paris Sphicas
What makes a force? A “law” of nature?
LHC Physics Goals
6
QFT: towards adding interactions


Can guess form of interaction (from data input)
Can appeal to symmetries (better…)
 They lead to conserved quantities; e.g.
the blob should behave
y
y'
the same irrespective
of coordinate frame
a
H
H
H  H  pi , xi   p i  
; x i 
xi
pi
Translation
invariance 
conservation of
H
d

H  0   xi  0  a   pi   0 (linear) momentum
dt  i

i xi
Paris Sphicas
LHC Physics Goals
7
Symmetries in nature


Extending previous analysis:
 Translations
 conservation(linear
momentum)

Rotations
 conservation(angular
momentum)

Translations in time
 conservation(energy)

Reflection
 conservation(parity)
Symmetries of the Lagrangian yield conserved quantities (Noether’s
Theorem)
 What is the symmetry behind electric-charge conservation?

Paris Sphicas
Local phase invariance of field.
LHC Physics Goals
8
Back to Quantum Mechanics

Imagine we have full equation describing full system:
21
 {+*}+ +.[uw]y = 0


In reality, it is Schrodinger/Klein-Gordon/Dirac equation
y a complex number  it can be written as y=a+ib=
|y|ei; where tan=b/a.

 is the “phase” of y.
All observables given by |y|2; system is invariant
under changes of .
 Also clear: in most general case, system is NOT
invariant under LOCAL changes in , i.e. x.
The incredible step:
 Postulate that system IS invariant under a local x



Paris Sphicas
We have to add something to the original equations
LHC Physics Goals
9
Electromagnetism, weak interaction, …


Electromagnetism: postulate that the world is invariant
under local (i.e. space-time dependent) “rotations”
 Have to add one new field with 4 numbers A

Its properties: it is massless, and it couples to the matter
fields via

This is the Lorentz force, and A is the photon.
Weak interaction: postulate that the world is invariant
under local rotation in TWO dimensions (SU(2))
 There are three possible independent rotations (the
fourth matrix is the identity)

Paris Sphicas
This introduces three new fields, which, eventually show up
as W+, W and Z0. (!!!)
LHC Physics Goals
10
Standard Model



Invariance of the world under phase changes in
SU(2)U(1) results in four bosons, W±, Z, 
 Thus the unification of Electromagnetism and the
Weak interaction into the Electroweak interaction
 Extremely successful description of all known
EM+Weak phenomena
But one basic problem remains: the symmetry MUST be
broken:
 The photon is massless
 The W,Z bosons are 80, 90 times the proton mass
Add symmetry-breaking terms by hand: no go
 Destroys the very principle (gauge invariance) via
which the Standard Model comes to existence
Paris Sphicas
LHC Physics Goals
11
Spontaneous Symmetry Breaking

Imagine a field with a potential with two minima:




Laws of nature
(potentialLagrangian
equations of motion)
right-left symmetric
Equilibrium state is not
Particle chooses one of
the two minima  leftright symmetry is broken
Laws are LR symmetric; but
the low-energy world need
not be!
Paris Sphicas
LHC Physics Goals
12
The Higgs mechanism


Solution to Symmetry Breaking: Higgs mechanism
 Introduce a field that obeys a potential that is
rotationally invariant (i.e. symmetric) and has multiple
minima away from a zero value of the field.
 lowest state of the theory: things roll to this minimum
(in one random direction)
 once this is done, the state of the system no longer
has the original symmetry...
The symmetry is lost as such, but appears as the mass
of the W and Z bosons.
This whole sequence is called "Spontaneous Symmetry
Breaking" (SSB)
Paris Sphicas
LHC Physics Goals
13
The Higgs Mechanism

With two independent fields
 Two “motions”

One up/down on potential;
massive
– Higgs boson

One on the plane; “massless”
mode that is lost (direction has
been chosen). The degree of
freedom appears as additional
degree of freedom of the other
boson
– Extra polarization state
– The boson becomes
massive!
Paris Sphicas
LHC Physics Goals
Thus were the W/Z
masses born in theory;
and discovered (at the
right mass) @ CERN in
1984.
14
Thoughts on the Standard Model



It’s beautiful, logically consistent
 It’s relatively low cost: adds one new particle (the
Higgs boson) only
Of course, it doesn’t tell us
 why three generations
 anything about gravity
 why neutrinos are (?) massless
 And many, many other things (Cosm. Constant etc)
But it is, with the possible exception of adding
Supersymmetry, the most powerful theory we have today
 But we need to find the Higgs; and theory does NOT
provide (precise) information on its mass
Paris Sphicas
LHC Physics Goals
15
The search for the Higgs (till 2005)


LEP (up to 2002) only machine capable of producing it
 MH>106 GeV/c2
2
 Some hasty evidence at 114.5 GeV/c ; significance
has dropped
Next: Tevatron @ Fermilab
 Run IIa:
2001-2003/4
 Run IIb (?):
2005 (?)
Paris Sphicas
LHC Physics Goals
16
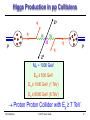
Higgs Production in pp Collisions
Z0
q
q
p
W
W
H
q
q
p
Z0
MH ~ 1000 GeV
EW ≥ 500 GeV
Eq ≥ 1000 GeV (1 TeV)
Ep ≥ 6000 GeV (6 TeV)
 Proton Proton Collider with Ep ≥ 7 TeV
Paris Sphicas
LHC Physics Goals
17
A machine for EWK Symmetry Breaking


Superconducting SuperCollider (SSC)
nd
 Today would have 2 -generation results
Large Hadron Collider
 Use existing LEP tunnel
D.Dicus, S. Willenbrock
Phys.Rev.D32:1642,1985
Not true any more (MT=175 GeV)
Paris Sphicas
LHC Physics Goals
18
pp cross section and min. bias

# of interactions/crossing:
 Interactions/s:




Lum = 1034 cm–2s–1=107mb–1Hz
s(pp) = 70 mb
Interaction Rate, R = 7x108 Hz
Events/beam crossing:



s(pp)70 mb
t = 25 ns = 2.5x10–8 s
Interactions/crossing=17.5
Not all p bunches are full


Approximately 4 out of 5 (only) are full
Interactions/”active” crossing = 17.5 x 3564/2835 = 23
Operating conditions (summary):
1) A "good" event containing a Higgs decay +
2)  20 extra "bad" (minimum bias) interactions
Paris Sphicas
LHC Physics Goals
19
pp collisions at 14 TeV at 1034 cm-2s-1
20 min bias
events
overlap
 HZZ
Z mm

H 4 muons:
the cleanest
(“golden”)
signature
Reconstructed tracks
with pt > 25 GeV
And this (not the
H though…)
repeats every
25 ns…
Paris Sphicas
LHC Physics Goals
20
SM Higgs

Decays & discovery
channels

Higgs couples to mf2



Low mass: b quarks
jets; resolution ~ 15%


Heaviest fermion (b quark)
always dominates
Until WW, ZZ thresholds
open
Only chance is EM energy
(use  decay mode)
Once MH>2MZ, use this

Paris Sphicas
W decays to jets or
lepton+neutrino (missing ET)
LHC Physics Goals
21
Low mass Higgs (MH<140 GeV/c2)

H: decay is rare (B~10-3)
 But with good resolution, one gets a
mass peak
 Motivation for LAr/PbWO4 calorimeters
 Resolution at 100 GeV, s1GeV

Paris Sphicas
S/B  1:20
LHC Physics Goals
22
Intermediate mass Higgs

HZZl+l– l+l– (l =e,m)
 Very clean


Resolution: better than 1 GeV
(around 100 GeV mass)
Valid for the mass range
130<MH<500 GeV/c2
Paris Sphicas
LHC Physics Goals
23
High mass Higgs

HZZ l+l– jet jet
 Need higher Branching
fraction (also  for the
highest masses ~ 800
GeV/c2)
 At the limit of statistics
Paris Sphicas
LHC Physics Goals
24
Higgs discovery prospects @ LHC

The LHC can probe the entire set of “allowed” Higgs
mass values
 in most cases a few months at low luminosity are
adequate for a 5s observation
CMS
Paris Sphicas
LHC Physics Goals
25
Problems with the Higgs

Quadratic divergence of its mass
m  p   m L  + Cg
2


2
2
2
2
L2
2
dk
2
p
L is a cutoff momentum
Put simply: why is the Higgs mass low?
Paris Sphicas
LHC Physics Goals
26
Supersymmetry (SUSY)

One possible solution:
 for every particle there exists a partner particle with ½
spin difference

With SUSY, infinities disappear:

Paris Sphicas
As long as Mp=Msp
LHC Physics Goals
27
Supersymmetry World


SUSY doubles the
particle spectrum
It must also be
broken
 To explain why
unseen till now
 If broken at
ESUSY:
m2 p2  
m 2 L2  + C ' g 2  2
E 2 SUSY
p
Paris Sphicas
dk 2
LHC Physics Goals
28
Supersymmetry and Unification

Couplings “run” with Q2:
 Loop diagrams (quantum
corrections) make the coupling
between the force and matter
particles dependent on the energy
at which the interaction occurs
 Extrapolating the couplings for the EM, WK and
strong interactions:
Without SUSY
Paris Sphicas
LHC Physics Goals
With SUSY
29
SUSY @ LHC

Simplest SUSY: mSUGRA
 A SUSY factory
Msp(GeV)
500
1000
2000
s (pb)
100
1
0.01
Evts/yr
106-107
~ 4-10
~5
10
102-103
M=500 GeV

Gauginos produced in their
decay; example: qLc20qL
Paris Sphicas
LHC Physics Goals
30
SUSY decays

Squarks & gluinos produced together with high s
 Gauginos produced in their decays; examples:



~ ~0
qLc2 qL (SUGRA
P5)
~
~
~0 _
q  g q c2 qq (GMSB G1a)
Two “generic” options with c0:
(1) c20 c10h (~ dominates if allowed)
(2) c20  c10l+l– or c20 l+l–

Charginos more difficult

Decay has  or light q jet
–
Options:



Paris Sphicas
Look for higgs (to bb)
Isolated (multi)-leptons
LHC Physics Goals
31

Multi-observations

Main peak from c~20c~10l+l–


Measure m as before
Also peak from Z0 through
c~ 0c~ 0Z0
2
1
Due to heavier gauginos
 P4 at “edge” of SB
 small m2 
(a) c± and c0 are
~ light
(b) strong mixing between
gauginos and Higgsinos

Events/(4 GeV/c2)
Some spectacular signatures
M(l+l-) (GeV/c2)

At P4 large Branching fractions to Z decays:
~
 e.g. B(c~c Z0)≈1/3; size of peak/P (Z)info on masses and
3
1.2
T
mixing of heavier gauginos (model-dependent)
Paris Sphicas
LHC Physics Goals
32
Observability of MSSM Higgses
MSSM Higgs bosons
4 Higgs observable
3 Higgs observable
2 Higgs observable
1 Higgs observable
h,A,H,H
h,A,H
h,H
5s contours
h
H,H
h,H
h,,H,H
h,A,H,H
h,H
Assuming decays
to SM particles
only
At least one Higgs boson will be found over the entire plane
Paris Sphicas
LHC Physics Goals
33
Gravity (I)

Traditional picture: gravity VERY weak
2
2
 Coupling runs as E /Mpl ;




scale set by Mpl given by G-1/2
Weakness “explained” by
large value of Mpl
Attempts to include gravity:
 So far: modify Standard Model
Novel idea
 Change gravity instead
» (Antoniadis, Lykken, Arkani-Hamed/Dimopoulos/Dvali)
GN  ( r1 )  ( r2 )
1 + e G exp  r12 / G 
V ( r )    dr1  dr2
r12

Paris Sphicas
Experimental limits on eG deteriorate fast with small G.
LHC Physics Goals
34
Gravity (II)

If gravity does change at some mass scale 1/R, the
Planck mass is a “mirage”

It’s an artifact, given by Mpl = M*(M*R)n/2
Paris Sphicas
LHC Physics Goals
35
Forces and number of dimensions


Number (D) of space-time dimensions  form of force
observed
2
 Electromagnetism: F~1/r because D=3+1
 For “ants” living in D=2+1 dimensions, E+M is actually
a F~1/r force
Side Conclusion: the running of the force changes in the
presence of additional dimensions
Paris Sphicas
LHC Physics Goals
36
Modifying Gravity (II)



Suppose extra dimensions do exist in nature
 e.g. could be curled up
R
 Then, at distance scales close to the radius, the
familiar law would get modified:
m1m2
m1m2
D  4; F  G 2
D  4 + n; F  k 2+n
r
r
Fundamental scale for quantum gravity: MS
-n+2
 Dimensions of k: [k] = M
 Equating the forces at a distance scale R we get
2/n
M
1
1  pl 
n
n +2
~R M
R~


G
MS  MS 
Scenario with MS~1 TeV:
-5 mm
 N=2  R ~ 0.4 mm; N=4  R ~ 10
Paris Sphicas
LHC Physics Goals
37
Extra (large) dimensions

Different models, different signatures:
miss+(jet/) (back-to-back)
 Channels with missing ET: ET
 Direct reconstruction of KK modes


Essentially a W’, Z’ search
Warped extra dimensions (graviton excitations)
e.g. Giudice, Ratazzi, Wells
(hep-ph/9811291)
Paris Sphicas
e.g. Hewett (hep-ph/9811356)
LHC Physics Goals
38
Extra (large) dimensions @ the LHC (I)

Basic signature: ETmiss+jet (back-to-back)


Results from theory papers based on similar signatures (e.g.
gravitino searches); instrumental bkg: same signature
Also +ETmiss; significant range in MD can be probed
Giudice, Ratazzi, Wells (hep-ph/9811291)
Paris Sphicas
LHC Physics Goals
39
KK resonances+angular analysis

If graviton excitations present, essentially a Z’ search.
 Added bonus: spin-2 (instead of spin-1 for Z)
Case shown*: Ge+e–
for M(G)=1.5 TeV
 Extract minimum s.B for
which spin-w hypothesis is
favored (at 90-95%CL)

100 fb–1
* B.Allanach,K.Odagiri,M.Parker,B.Webber
JHEP09 (2000)019
Paris Sphicas
LHC Physics Goals
40
Black Holes at the LHC (?)

Always within context of “TeV-scale gravity”
 Semi-classical argument: two partons approaching with impact
parameter < Schwarzschild radius, RS  black hole


(Myers & Perry; Ann. Phys 172, 304 (1996)
From dimensions: s(MBH)~pRS2; MP~1TeV  s~400 pb (!!!)


RS ~ 1/MP (MBH/MP)(1/d+1)
Absence of small coupling like a
LHC, if above threshold, will be a Black Hole Factory:

At minimum mass of 5 TeV: 1Hz production rate
Dimopoulos &
Landsberg
hep-ph/0106295
Assumptions:
MBH>>MP; in order to avoid true
quantum gravity effects… clearly not
the case at the LHC – so caution
Giddings & Thomas
hep-ph/0106219
Paris Sphicas
LHC Physics Goals
41
Summary


Higgs is still missing
 Symmetry Breaking in the SM (and beyond!) still not
understood
Physics at the LHC (can be) extremely rich
 SM Higgs (if there) in the pocket


Supersymmetry (if there) ditto


Now turning to measurements of couplings, etc.
Can perform numerous accurate measurements
Large com energy: new thresholds

Compositeness, new bosons, large extra dimensions within
reach
May even have a first look at gravitational effects
Just need to build machine/experiments
 And their electronics


Paris Sphicas
LHC Physics Goals
42
Backups
Local phase invariance

QM: invariance under changes of the phase of y
i
 y  y e ; all observables unaffected
 True also with relativistic additions (KG & Dirac eqns)
2

f
2
2
2
E  p + m   2    2 + m 2 f   m  mf + m 2 f  0
t
 KG Lagrangian (density):
L  (1 / 2) mf  mf  (1 / 2)m 2f 2

Gauge principle:
 postulate/demand that the world (i.e. its Lagrangian) is invariant
under local changes of phase; f  f eiq(x)

derivatives in equations of motion spoil simple phase cancellation:

Have to add new field Am in L; cook it up so L is invariant:
 mf  eiq ( x )  mf + iqeiq ( x )f  m
L  1 / 2  m + iqAm f  m + iqAm f  1 / 2m 2f 2

Paris Sphicas
i.e. demand:
Am  Am   m
and L IS invariant now
LHC Physics Goals
44
Quantum Electrodynamics

The “derivation” of electromagnetism: same exercise
+  Interactions between e e ; spin-1/2 fields


L  y i m  m  my
Dirac Lagrangian
Invariance under rotations in U(1), i.e. yyeiq(x) requires
adding a field A that cancels derivatives, i.e.
L  y [i m  m + iqAm   m]y ; Am  Am   m

The fields A and y now interact:


Lint  qy  m Amy
Which is precisely the interaction term in the Maxwell Lagrangian
1 m
L
F Fm  J m Am (with J m  qy  my )
16p
 Which gives a matter-A-matter interaction with Force Law


  0 A 
  
F  q  A +  + qv    A
t 

m
Photon is massless (no A A term)
m

Paris Sphicas
Forbidden by gauge invariance
LHC Physics Goals
45
Weak Interactions

Two particle species (e.g. lepton, neutrino)
L  y 1 [i m  m  m]y 1 +y 2 [i m  m  m]y 2

Defining the doublet (y1 y2)
L  y [i m  m  M ]y ; M  diag m1 , m2 

General change of phase: yUy; with U unitary





Any unitary matrix can be written U=exp(iH); H: hermitian
Most general 2x2 Hermitian matrix needs 4 real numbers:
 
 
H   I + a   U  exp i  exp ia  
New phase change: SU(2)
Localize it  gauge theory for weak interaction (W+, W-, Z0)
Invariance of the world under phase changes in SU(2)U(1) results
in four bosons, W±, Z, 
 Thus the unification of Electromagnetism and the Weak
interaction into the Electroweak interaction
Paris Sphicas
LHC Physics Goals
46
Information (limits) on MH: summary

Triviality bound
 4p 2 v 2 
L  M H exp 
2 
 3M H 
<f0>0
3GF 2
2
2
2


MH 
F
log
L
/
v
2
8p

Precision EWK measurements

LEP direct search:
MH>114 GeV/c2
Paris Sphicas
LHC Physics Goals
47
Gravity tests

Experimental Limits on eG-G:
Paris Sphicas
LHC Physics Goals
48