* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Diffraction topography wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Atmospheric optics wikipedia , lookup
Optical amplifier wikipedia , lookup
Birefringence wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Fourier optics wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Reflector sight wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Optical rogue waves wikipedia , lookup
Fiber-optic communication wikipedia , lookup
Confocal microscopy wikipedia , lookup
Ellipsometry wikipedia , lookup
Reflecting telescope wikipedia , lookup
3D optical data storage wikipedia , lookup
Nonimaging optics wikipedia , lookup
Photon scanning microscopy wikipedia , lookup
Optical coherence tomography wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
Optical aberration wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Laser beam profiler wikipedia , lookup
Retroreflector wikipedia , lookup
Passive optical network wikipedia , lookup
Silicon photonics wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
CHAPTER 1---- Optical Resonator
Chapter 1
Optical Resonator
Fundamentals of Photonics
2017/5/24
1
CHAPTER 1---- Optical Resonator
What is an optical resonator?
An optical resonator, the optical counterpart of an electronic resonant
circuit, confines and stores light at certain resonance frequencies. It may be
viewed as an optical transmission system incorporating feedback; light
circulates or is repeatedly reflected within the system, without escaping.
(b)
(a)
(d)
(c)
Fundamentals of Photonics
2017/5/24
2
CHAPTER 1---- Optical Resonator
Contents:
• 1.1 Brief review of matrix optics
• 1.2 Planar Mirror Resonators
– Resonator Modes
– The Resonator as a Spectrum Analyzer
– Two- and Three-Dimensional Resonators
• 1.3 Spherical-Mirror Resonators
– Ray confinement
• 1.4 Gaussian waves and its characteristics
– The Gaussian beam
– Transmission through optical components
– Gaussian Modes
– Resonance Frequencies
– Hermite-Gaussian Modes
– Finite Apertures and Diffraction Loss
Fundamentals of Photonics
2017/5/24
3
CHAPTER 1---- Optical Resonator
1.1 Brief review of Matrix optics
Light propagation in a optical system, can use a matrix M,
whose elements are A, B, C, D, characterizes the optical system
Completely ( known as the ray-transfer matrix.) to describe the
rays transmission in the optical components.
One can use two parameters:
y2 Ay1 B1
2 Cy1 D1
y2 Ay1 B1
the high
:
the angle above z axis
y2 A B y1
C D
1
2
2 Cy1 D1
Fundamentals of Photonics
y:
2017/5/24
4
CHAPTER 1---- Optical Resonator
y2 y1 d tg1
2 1
2
1
For the paraxial rays
y2
y1
tg
y2 1 d y1
0 1
1
2
y2,2
-2
y1,1
1
y2 y1
2
2 y1 1
R
y1
-R
Along z upward angle is positive,
and downward is negative
Fundamentals of Photonics
2017/5/24
5
CHAPTER 1---- Optical Resonator
Free-Space Propagation
Refraction at a Planar Boundary
1
M
0
1 d
M
0 1
Refraction at a Spherical Boundary
1
M (n2 - n1 )
n2 R
Transmission Through a Thin Lens
0
n1
n2
Reflection from a Planar Mirror
1
M 1
f
0
1
Reflection from a Spherical Mirror
1 0
M
0 1
Fundamentals of Photonics
0
n1
n2
2017/5/24
1
M 2
R
0
1
6
CHAPTER 1---- Optical Resonator
A Set of Parallel Transparent Plates
1
M
0
di
n
i
1
Matrices of Cascaded Optical Components
M M1M 2 ....M N
Fundamentals of Photonics
2017/5/24
7
CHAPTER 1---- Optical Resonator
Periodic Optical Systems
The reflection of light between two parallel mirrors forming an optical
resonator is a periodic optical system is a cascade of identical unit system.
Difference Equation for the Ray Position
A periodic system is composed of a cascade of identical unit systems
(stages), each with a ray-transfer matrix (A, B, C, D). A ray enters the system
with initial position y, and slope 8,. To determine the position and slope (y,,,,
0,) of the ray at the exit of the mth stage, we apply the ABCD matrix m times,
ym A
C
m
Fundamentals of Photonics
m
B y0
D 0
2017/5/24
ym1 Aym B m
m1 Cym D m
8
CHAPTER 1---- Optical Resonator
ym1 Aym B m
m1 Cym D m
From these equation, we have
ym 1 - Aym
B
y - Aym 1
m 1 m 2
B
m
And then:
ym 2 2bym1 - F 2 ym
where
linear differential equations
A D 2
b
, F AD - BC det M
2
Fundamentals of Photonics
2017/5/24
9
CHAPTER 1---- Optical Resonator
If we assumed:
y m y0 h m
So that, we have
If we defined
h 2 - 2bh F 2 0
h b i F 2 - b2
cos-1 b F
We have b F cos , F 2 - b2 F sin
then
h F (cos i sin ) Fei
ym y0 F m e im
A general solution may be constructed from the two solutions with positive
and negative signs by forming their linear combination. The sum of the two
exponential functions can always be written as a harmonic (circular) function
ym y0 F m sin(m 0 ) ymax F m sin(m 0 )
Fundamentals of Photonics
2017/5/24
10
CHAPTER 1---- Optical Resonator
If F=1, then ym ymax sin(m 0 )
Condition for a Harmonic Trajectory: if ym be harmonic, the cos-1b must
be real, We have condition
b 1
or
A D
1
2
The bound b 1 therefore provides a condition of stability (boundedness) of
the ray trajectory
If, instead, |b| > 1, is then imaginary and the solution is a
hyperbolic function (cosh or sinh), which increases without bound.
A harmonic solution ensures that y, is bounded for all m, with a
maximum value of ymax. The bound |b|< 1 therefore provides a
condition of stability (boundedness) of the ray trajectory.
Fundamentals of Photonics
2017/5/24
11
CHAPTER 1---- Optical Resonator
Condition for a Periodic Trajectory
Unstable b>1
Stable and periodic
Stable nonperiodic
The harmonic function is periodic in m, if it is possible to find an integer
s such that ym+s = ym, for all m. The smallest such integer is the period.
The necessary and sufficient condition for a periodic trajectory is:
s = 2pq,
where q is an integer
Fundamentals of Photonics
2017/5/24
12
CHAPTER 1---- Optical Resonator
EXERCISE : A Periodic Set of Pairs of Different Lenses. Examine the trajectories of
paraxial rays through a periodic system composed of a set of lenses with alternating focal
lengths f1 and f2 as shown in Fig. Show that the ray trajectory is bounded (stable) if
0 (1 1
M 1
f 2
0
1
1
d
1
1 0 1
f1
Fundamentals of Photonics
d
d
)(1 ) 1
2 f1
2 f2
d
1
0
f1
1 d
1 0 1 d
1 1
-
f1 f 2 f1 f 2
2017/5/24
d
d
d
- (1 - )(1 - )
f2
f1
f2
d2
2d f1
13
CHAPTER 1---- Optical Resonator
Home works
4 X 4 Ray-Transfer Matrix for Skewed Rays. Matrix methods may be
generalized to describe skewed paraxial rays in circularly symmetric
systems, and to astigmatic (non-circularly symmetric) systems. A ray
crossing the plane z = 0 is generally characterized by four variables-the
coordinates (x, y) of its position in the plane, and the angles (e,, ey) that its
projections in the x-z and y-z planes make with the z axis. The emerging ray
is also characterized by four variables linearly related to the initial four
variables. The optical system may then be characterized completely, within
the paraxial approximation, by a 4 X 4 matrix.
(a) Determine the 4 x 4 ray-transfer matrix of a distance
d in free space.
(b) Determine the 4 X 4 ray-transfer matrix of a thin
cylindrical lens with focal length f oriented in the y
direction. The cylindrical lens has focal length f for rays
in the y-z plane, and no focusing power for rays in the xz plane.
Fundamentals of Photonics
2017/5/24
14
CHAPTER 1---- Optical Resonator
1.2 Planar Mirror Resonators
This simple one-dimensional
resonator is known as a
Fabry-Perot etalon.
A. Resonator Modes
Resonator Modes as Standing Waves
A monochromatic wave of frequency v has a wavefunction as
u (r , t ) Re{U (r ) exp( j 2p vt )}
Represents the transverse component of electric field.
The complex amplitude U(r) satisfies the Helmholtz equation;
Where k =2pv/c called wavenumber, c speed of light in the medium
Fundamentals of Photonics
2017/5/24
15
CHAPTER 1---- Optical Resonator
the modes of a resonator must be the solution of Helmholtz equation
with the boundary conditions:
z 0
U (r ) 0
z d
So that the general solution is standing wave:
U (r ) A sin kz
d
With boundary condition, we have kd qp
F
c
2d
q q 1
qp
kq
d
c
, q 1, 2,...,
2d
c
F
2d
Resonance frequencies
Fundamentals of Photonics
q q
2017/5/24
16
CHAPTER 1---- Optical Resonator
lq
The resonance wavelength is:
The length of the resonator, d = q lq /2,
wavelength
Attention:
c c0 / n
c
q
2d
q
is an integer number of half
Where n is the refractive index in the resonator
Resonator Modes as Traveling Waves
A mode of the resonator: is a self-reproducing wave, i.e., a wave that reproduces
itself after a single round trip , The phase shift imparted by a single round trip of
propagation (a distance 2d) must therefore be a multiple of 2p.
k 2d
Fundamentals of Photonics
4p n
l0
d
4p
d q 2p
c
2017/5/24
q= 1,2,3,…
17
CHAPTER 1---- Optical Resonator
Density of Modes (1D)
The density of modes M(v), which is the number of
modes per unit frequency per unit length of the resonator, is
M ( )
4
c
For 1D resonator
The number of modes in a resonator of length d within the frequency
interval v is:
4
d
c
This represents the number of degrees of freedom for the optical waves
existing in the resonator, i.e., the number of independent ways in which
these waves may be arranged.
Fundamentals of Photonics
2017/5/24
18
CHAPTER 1---- Optical Resonator
Losses and Resonance Spectral Width
The magnitude ratio of two consecutive phasors is the round-trip
amplitude attenuation factor r introduced by the two mirror reflections and
by absorption in the medium. Thus:
Mirror 1
U1 hU 0 e U 0 e
- i
-i
4p nd
l
U 0 e-i 2 kdU 0
U2
So that, the sum of the sequential reflective light with field of
U U 0 U1 U 2 U3 ... U 0 (1 h h2 h3 ...)
IU
2
U0
2
1- e
finally, we have
- i 2
I
I0
(1 - 2 cos )
2
I0
U0
U1
U0
(1 - h)
(1 - ) 2 4 sin 2
2
I max
,
1 (2F / p ) 2 sin 2 ( / 2)
p 1/ 2
F
1-
Fundamentals of Photonics
Mirror 2
U3
2017/5/24
I max
I0
(1 - ) 2
Finesse of the resonator
19
CHAPTER 1---- Optical Resonator
The resonance spectral peak has a full width of half maximum (FWHM):
c
4p d
F
F
I max
I max
4p d
I
I
We have
Due to
1 (2F / p ) 2 sin 2 (p / F ) min 1 (2F / p ) 2
c
where F c 2d q q F , q 1, 2,...,
c
F
2d
Fundamentals of Photonics
2017/5/24
F
F
20
CHAPTER 1---- Optical Resonator
Spectral response of Fabry-Perot Resonator
The intensity I is a periodic function of with period 2p. The dependence of I
on , which is the spectral response of the resonator, has a similar periodic
behavior since = 4pd/c is proportional to . This resonance profile:
I
I max
1 (2 F / p ) 2 sin 2 (p / F )
The maximum I = Imax, is achieved at the
q q F , q 1, 2,...,
resonance frequencies
whereas the minimum value
I min
The FWHM of the resonance peak is
Fundamentals of Photonics
2017/5/24
I max
1 (2 F / p ) 2
c
4p d
F
F
21
CHAPTER 1---- Optical Resonator
Sources of Resonator Loss
•
•
Absorption and scattering loss during the
round trip: exp (-2asd)
Imperfect reflectance of the mirror: R1, R2
R1 R2 exp(-2 s d )
2
Defineding that
2 exp(-2 r d )
1
1
r s
ln
2d
R1 R2
we get:
ar is an effective overall
distributed-loss coefficient,
which is used generally in the
system design and analysis
Fundamentals of Photonics
r s
m1
2017/5/24
1
1
ln
s m1 m 2
2d R1 R2
1
1
ln
2d R1
m1
1
1
ln
2d R1
22
CHAPTER 1---- Optical Resonator
If the reflectance of the mirrors is very
high, approach to 1, so that
The above formula can approximate as
r s
R1 R2 R 1
m1
1
1
ln
s m1 m 2
2d R1 R2
1 - R1 1 - R2
1- R
m2
2d
2d
2d
r s
1- R
d
The finesse F can be expressed as a function of the effective loss coefficient ar,
F
p exp(- r d / 2)
1 - exp(- r d )
Because ard<<1, so that exp(-ard)=1-ard, we have:
F
p
r d
The finesse is inversely proportional to the loss factor rd
Fundamentals of Photonics
2017/5/24
23
CHAPTER 1---- Optical Resonator
Photon Lifetime of Resonator
The relationship between the resonance linewidth and the resonator loss
may be viewed as a manifestation of the time-frequency uncertainty relation.
Form the linewidth of the resonator, we have
c
c / 2d
r
p / r d 2p
Because ar is the loss per unit length, car is the
loss per unit time, so that we can Defining the
characteristic decay time as the resonator lifetime
or photon lifetime
The resonance line broadening is seen to be
governed by the decay of optical energy arising
from resonator losses
Fundamentals of Photonics
2017/5/24
p
1
c r
1
2p p
24
CHAPTER 1---- Optical Resonator
The Quality Factor Q
The quality factor Q is often used to characterize electrical resonance circuits
and microwave resonators, for optical resonators, the Q factor may be determined
by percentage of that stored energy to the loss energy per cycle:
Q
2p ( storedenergy)
Large Q factors are associated with low-loss resonators
energylosspercycle
For a resonator of loss at the rate cr (per unit time), which is equivalent to the rate
cr /0 (per cycle), so that
Q 2p 1
(c r / 0 )
c r 2p
Q
0
The quality factor is related to the resonator lifetime (photon lifetime)
1
p 1 c
r
2p
Q 2p 0 p
The quality factor is related to the finesse of the resonator by Q
Fundamentals of Photonics
2017/5/24
0
F
F
25
CHAPTER 1---- Optical Resonator
• In summary, three parameters are convenient for
characterizing the losses in an optical resonator:
– the finesse F
– the loss coefficient r (cm-1),
– photon lifetime p = 1/cr, (seconds).
• In addition, the quality factor Q can also be used for this
purpose
Fundamentals of Photonics
2017/5/24
26
CHAPTER 1---- Optical Resonator
B. The Resonator as a Spectrum Analyzer
Transmission of a plane wave across a planar-mirror resonator (Fabry-Perot etalon)
t1
r1
r2
t2
T ( )
It
I
T ( )
Tmax
1 (2F / p ) 2 sin 2 (p / F )
Where:
U2
Tmax
U0
Fundamentals of Photonics
2
(1 - )
2
, t t1t2 , 1 2
p 1/2
F
1-
U1
Mirror 1
t
Mirror 2
The change of the length of the cavity
will change the resonance frequency
q d
qc
q - 2 d 2d
d
2017/5/24
27
CHAPTER 1---- Optical Resonator
C. Two- and Three-Dimensional Resonators
• Two-Dimensional Resonators
q yp
qp
ky
, k z z , q y 1, 2,..., qz 1, 2,...,
d
d
k 2 k y2 k z2 (
2p 2
)
c
• Mode density
Determine an approximate expression for the number of modes in a
two-dimensional resonator with frequencies lying between 0 and ,
assuming that 2p/c >> p/d, i.e. d >>l/2, and allowing for two
orthogonal polarizations per mode number.
Fundamentals of Photonics
2017/5/24
M ( )
4p
c2
28
CHAPTER 1---- Optical Resonator
Three-Dimensional Resonators
Physical space resonator
Wave vector space
q yp
qxp
qp
kx
, ky
, k z z , qx , q y , qz 1, 2,...,
d
d
d
k 2 k x2 k y2 k z2 (
2p 2
)
c
Mode density
M ( )
8p
c3
2
Fundamentals of Photonics
The number of modes lying in the frequency interval
between 0 and v corresponds to the number of
points lying in the volume of the positive octant of a
sphere of radius k in the k diagram
2017/5/24
29
CHAPTER 1---- Optical Resonator
1.2 Optical resonators and stable condition
A. Ray Confinement of spherical resonators
The rule of the sign: concave mirror (R < 0), convex (R > 0). The
planar-mirror resonator is R1 = R2=∞
z
d
The matrix-optics methods introduced which are valid only for paraxial rays, are
used to study the trajectories of rays as they travel inside the resonator
Fundamentals of Photonics
2017/5/24
30
CHAPTER 1---- Optical Resonator
C. Stable condition of the resonator
For paraxial rays, where all angles are small, the relation between
(ym+1, m+1) and (ym, m) is linear and can be written in the matrix form
y1
- 1
A B 1
z C D 2
R1
2
y2
ym1 A B ym
C D
m
m1
R2
R1
0
reflection
from a
mirror of
radius R1
y0
d
Attention here: we just take general case
spherical so doesn’t take the sign
Fundamentals of Photonics
0 1 d 1
1 0 1 R22
2017/5/24
0 1 d
1 0 1
reflection
from a
mirror of
radius R2
propagation a distance
d through free space
31
CHAPTER 1---- Optical Resonator
A 1 2d
R2
B 2d (1 d
C 2
R1
D 2d
2
R1
R2
R2
( 2d
det M Ad - BC 1 F 2
)
4d
R1
ym ymax sin(m 0 )
d
d
b ( A D) / 2 2 1 1 - 1
R1 R2
R1 R2
1)(2d
R1
1)
It the way is harmonic, we need cos-1b must be real, that is
b 1 b ( A D ) / 2 2 1
d
d
1
-1 1
R1 R2
for g1=1+d/R1; g2=1+d/R2
d
d
0 1
1
1
R1
R2
Fundamentals of Photonics
2017/5/24
0 g1 g 2 1
32
CHAPTER 1---- Optical Resonator
resonator is in conditionally stable, there will be:
d
d
0 1 1 1
R1 R2
0 g1 g 2 1
In summary, the confinement condition for paraxial rays in a sphericalmirror resonator, constructed of mirrors of radii R1,R2 seperated by a
distance d, is 0≤g1g2≤1, where g1=1+d/R1 and g2=1+d/R2
For the concave R is negative, for the convex R is positive
Fundamentals of Photonics
2017/5/24
33
CHAPTER 1---- Optical Resonator
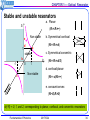
Stable and unstable resonators
a. Planar
g2
(R1= R2=∞)
e
1
Non stable
d
b. Symmetrical confocal
(R1= R2=-d)
a
c. Symmetrical concentric
stable
b
-1
0
1
g1
(R1= R2=-d/2)
d. confocal/planar
c
Non stable
(R1= -d,R2=∞)
e. concave/convex
(R1<0,R2>0)
d/(-R) = 0, 1, and 2, corresponding to planar, confocal, and concentric resonators
Fundamentals of Photonics
2017/5/24
34
CHAPTER 1---- Optical Resonator
The stable properties of optical resonators
Crystal state resonators
g1 g2 0
or
g1 g2 1
a. Planar
(R1= R2=∞)
b. Symmetrical confocal
Stable
(R1= R2=-d)
c. Symmetrical concentric
unstable
Fundamentals of Photonics
(R1= R2=-d/2)
2017/5/24
35
CHAPTER 1---- Optical Resonator
Unstable resonators
Unstable cavity corresponds to the high loss
g1 g2 0
g1 g2 1
or
a. Biconvex resonator
d
b. plan-convex resonator
c. Some cases in plan-concave resonator
When R2<d, unstable
R1
d. Some cases in concave-convex resonator
When R1<d and R1+R2=R1-|R2|>d
d
e. Some cases in biconcave resonator
g1 g 2 (1 d / R1 )(1 d / R2 ) 0
g1 g 2 (1 d / R1 )(1 d / R2 ) 1
Fundamentals of Photonics
R1 R2 d
2017/5/24
36
CHAPTER 1---- Optical Resonator
1.2 Gaussian waves and its characteristics
A. Gaussian beam
Helmholtz equation
2U k 2U 0
Normally, a plan wave (in z direction) will be
U U 0 exp{-i(k r)} U 0 exp(-ikz )
When amplitude is not constant the wave is
U A( x, y, z ) exp(-ikz )
An axis symmetric wave in the amplitude
U A(r ) exp(-ikz )
frequency
Fundamentals of Photonics
2p
Wave vector
2017/5/24
z
k
2p
l
37
CHAPTER 1---- Optical Resonator
Paraxial Helmholtz equation
Substitute the U into the Helmholtz equation we have:
A
A - i 2k
0
z
where
2
T
2
T
2
2
2 2
x y
A1
2
One simple solution is spherical wave: A(r ) exp(- jk ) 2 x 2 y 2
z
2z
The other solution is Gaussian wave:
W0
2
2
U (r ) A0
exp[- 2 ]exp[-ikz - ik
i ( z )]
W ( z)
W ( z)
2 R( z )
where
z
z 2 1/ 2
) ] ( z ) tan -1
z0 is Rayleigh range
z0
z0
1
1
l
l z0 1/2
z0 2
i
R( z ) z[1 ( ) ] W0 ( ) W ( z ) z 0 W (0) q( z ) R( z ) pW 2 ( z )
W ( z ) W0 [1 (
z
p
q parameter
Fundamentals of Photonics
2017/5/24
38
CHAPTER 1---- Optical Resonator
Electric field of Gaussian wave propagates in z dirextion
A0
-( x 2 y 2 )
x2 y 2
E ( x, y, z )
exp[
] exp[ -ik (
z) i ( z)]
2
W ( z)
W ( z)
2 R( z )
Beam width at z
W ( z ) W0 [1 (
z 2 1/ 2
) ]
z0
W0 W (0)
Waist width
pW02 2
z0 2
pW02
Radii of wave front at z R( z ) z[1 (
) ] z[1 ( ) ], z0
lz
z
l
Phase factor
Fundamentals of Photonics
( z ) arctan
2017/5/24
lz
-1 z
tg
p W02
z0
39
CHAPTER 1---- Optical Resonator
Gaussian beam at z=0
A0
r2
E ( x, y,0)
exp[ - 2 ] where r 2 x 2 y 2
W0
W0
Beam width: W ( z ) W0 [1 (
E
A0
W0
z 2 1/ 2
) ]
will be minimum
z0
A0
eW0
2 2
p
W
0
wave front: lim R ( z ) lim z 1
z 0
z 0
l z
-W0
W0
at z=0, the wave front of Gaussian beam is a plan
surface, but the electric field is Gaussian form
W0 is the waist half width
Fundamentals of Photonics
2017/5/24
40
CHAPTER 1---- Optical Resonator
B. The characteristics of Gaussian beam
Beam
radius
z
Gaussian beam is a axis symmetrical wave, at z=0
phase is plan and the intensity is Gaussian form,
at the other z, it is Gaussian spherical wave.
Fundamentals of Photonics
2017/5/24
41
CHAPTER 1---- Optical Resonator
Intensity of Gaussian beam
Intensity of Gaussian beam
z=0
y
W0 2
2
I ( , z) I0[
] exp[- 2 ]
W ( z)
W ( z)
z=z0
z=2z0
y
y
x
I
I0
I
I0
1
0
x
-1
0
1
W0
I
I0
1
0
x
-1
0
1
W0
1
0
-1
0
1
W0
The normalized beam intensity as a function of the radial distance at different axial distances
Fundamentals of Photonics
2017/5/24
42
CHAPTER 1---- Optical Resonator
On the beam axis ( = 0) the intensity
I (0, z ) I 0 [
W0 2
I0
]
z
W ( z)
1 ( )2
z0
I
I0
1
1
0.5
- zo
0
0
zo
z
The normalized beam intensity I/I0
at points on the beam axis (p=0) as a function of z
Fundamentals of Photonics
2017/5/24
43
CHAPTER 1---- Optical Resonator
Power of the Gaussian beam
The power of Gaussian beam is calculated by the integration
of the optical intensity over a transverse plane
P
1
I 0p W02
2
So that we can express the intensity of the beam by the power
2P
2 2
I ( , z)
exp[- 2 ]
2
pW ( z )
W ( z)
The ratio of the power carried within a circle of radius r. in the
transverse plane at position z to the total power is
202
1 0
I ( , z )2p d 1 - exp[- 2 ]
P 0
W ( z)
Fundamentals of Photonics
2017/5/24
44
CHAPTER 1---- Optical Resonator
Beam Radius W ( z ) W0 [1 (
W
z 2 1/ 2
W ( z ) 0 z 0 z
) ]
z0
z0
W(z)
Beam
waist
2W 0
W0
-z0
0
z
z0
The beam radius W(z) has its minimum value W0 at the waist (z=0)
reaches 2W0 at z=±z0 and increases linearly with z for large z.
Beam Divergence
1
dW ( z ) 2lz p 2W02 2
2 2
2 2
[(
) z ]
dz
pW0
l
Fundamentals of Photonics
2017/5/24
0
l
p W0
45
CHAPTER 1---- Optical Resonator
The characteristics of divergence angle
z 0, 2 0
p W02
z
, 2 2l / p W0
l
z , 2
2l
2W ( z )
or 2 lim
x
p W0
z
Let’s define f=z0
pW02
as the confocal parameter of Gaussian beam f z0
l
The physical means of f :the half distance between two section of width
fl
z2
2
(1 2 )
p
f
2W ( z )
l
2 lim
lim
2
z
z
z
z
fp
Fundamentals of Photonics
2017/5/24
46
CHAPTER 1---- Optical Resonator
Depth of Focus
Since the beam has its minimum width at z = 0, it achieves its best focus at the
plane z = 0. In either direction, the beam gradually grows “out of focus.” The
axial distance within which the beam radius lies within a factor 20.5 of its
minimum value (i.e., its area lies within a factor of 2 of its minimum) is known
as the depth of focus or confocal parameter
20.5o
o
0
z
2 z0
2p W02
l
2zo
The depth of focus of a Gaussian beam.
Fundamentals of Photonics
2017/5/24
47
CHAPTER 1---- Optical Resonator
Phase of Gaussian beam
The phase of the Gaussian beam is,
( , z ) kz - ( z )
R( z ) z[1 (
k
2 R( z )
2
z0 2
) ]
z
On the beam axis (p = 0) the phase
(0, z ) kz - ( z )
kz
Phase of plan wave
( z)
an excess delay of the wavefront in comparison with a
plane wave or a spherical wave
The excess delay is –p/2 at z=-∞, and p/2 at z= ∞
The total accumulated excess retardation as the wave travels from z
= -∞ to z =∞is p. This phenomenon is known as the Guoy effect.
Fundamentals of Photonics
2017/5/24
48
CHAPTER 1---- Optical Resonator
Wavefront
pW02 2
f2
R( z ) z[1 (
) ] z
lz
z
Confocal field and its equal phase front
Fundamentals of Photonics
2017/5/24
49
CHAPTER 1---- Optical Resonator
Parameters Required to Characterize a
Gaussian Beam
How many parameters are required to describe a plane wave, a spherical
wave, and a Gaussian beam?
The plane wave is completely specified by its complex amplitude and
direction.
The spherical wave is specified by its amplitude and the location of its origin.
The Gaussian beam is characterized by more parameters- its peak
amplitude [the parameter A, its direction (the beam axis), the location of its
waist, and one additional parameter: the waist radius W0 or the Rayleigh
range zo,
q-parameter q(z) is sufficient for characterizing a Gaussian beam of known
peak amplitude and beam axis
If the complex number q(z) = z + iz0, is known
the real part of q(z) z is the beam waist place
the imaginary parts of q(z) z0 is the Rayleigh range
Fundamentals of Photonics
2017/5/24
50
CHAPTER 1---- Optical Resonator
Parameters required to describe a Gaussian beam
The Gaussian beam is characterized by : its peak amplitude [the
parameter A, its direction (the beam axis), the location of its waist, and
one additional parameter: the waist radius W0 or the Rayleigh range zo
q parameter is an sufficient factor to characteristic a Gaussian beam
of known peak amplitude and beam axis
1
1
l
-i
q( z ) R( z ) p W 2 ( z )
1
1
q( z ) z iz0
If the complex number q(z) = z + iz0, is known, the distance z to the
beam waist and the Rayleigh range z0. are readily identified as the real
and imaginary parts of q(z).
Fundamentals of Photonics
2017/5/24
51
CHAPTER 1---- Optical Resonator
C. TRANSMISSION THROUGH OPTICAL
COMPONENTS
a). Transmission Through a Thin Lens
kz k
2
2R
- - k
2
2f
kz k
2
2R '
-
1 1 1
R' R f
1 1 1
-
R R' f
Notes:
R is positive since the wavefront of the incident beam is diverging and R’
is negative since the wavefront of the transmitted beam is converging.
Fundamentals of Photonics
2017/5/24
52
CHAPTER 1---- Optical Resonator
In the thin lens transform, we have
W0 , z1 , f
W W '
1 1 1
R' R f
If we know W0, Z1, f, we can get
p W 2 2 -1
W W [1 (
) ]
lR '
l R ' 2 -1
- z ' R '[1 (
) ]
2
pW
'2
0
2
The minus sign is due to the waist lies to the right of the lens.
Fundamentals of Photonics
2017/5/24
53
CHAPTER 1---- Optical Resonator
W0 '
W
[1 (p W 2 / l R ')2 ]1/ 2
because R z[1 ( z0 / z ) 2 ]
-z '
and
R'
1 (p R '/ lW 2 ) 2
W W0 [1 ( z / z0 ) 2 ]1/2
W0 ' MW0
Waist radius
Waist location
( z '- f ) M ( z - f )
Depth of focus
2 z0' M 2 (2 z0 )
Divergence angle
,
magnification
Fundamentals of Photonics
2
2 0
M
Mr
M
(1 r 2 )1/ 2
2 0'
2017/5/24
The beam waist is
magnified by M, the
beam depth of focus is
magnified by M2, and the
angular divergence is
minified by the factor M.
where r
z0
f
Mr
z- f
z- f
54
CHAPTER 1---- Optical Resonator
Limit of Ray Optics
Consider the limiting case in which (z - f) >>zo, so that the lens is well
outside the depth of focus of the incident beam, The beam may then
be approximated by a spherical wave, thus
z0
r
0
z- f
z
and
M Mr
z’
W0 ' MW0
1 1 1
z' z f
2W0’
2W0
M Mr
f
z- f
The magnification factor Mr is that based on ray optics. provides that M < Mr,
the maximum magnification attainable is the ray-optics magnification Mr.
Fundamentals of Photonics
2017/5/24
55
CHAPTER 1---- Optical Resonator
b). Beam Shaping
Beam Focusing If a lens is placed at the waist of a Gaussian beam, so z=0, then
W0 '
z'
W0
[1 ( z0 / f ) 2 ]1/ 2
f
1 ( f / z0 ) 2
If the depth of focus of the incident beam 2z0, is much longer than the
focal length f of the lens, then W0’= ( f/zo)Wo. Using z0 =pW02/l, we obtain
W0 '
l
p W0
f 0 f
z' f
The transmitted beam is then focused at the lens’ focal plane as
would be expected for parallel rays incident on a lens. This occurs
because the incident Gaussian beam is well approximated by a plane
wave at its waist. The spot size expected from ray optics is zero
Fundamentals of Photonics
2017/5/24
56
CHAPTER 1---- Optical Resonator
Focus of Gaussian beam
W'
2
0
W02
W02 2
z
(1 - ) ( )
f
lf
2
For given f, W '0 changes as
•when
z1 0
•when
•when
•when
z1 f
W '02 decreases as z decreases
W0 ' reaches minimum, and M<1, for f>0, it is focal effect
z1 f
,
W0 ' increases as z increases
z1 f
z f
the bigger z, smaller f, better focus
W '0 reaches maximum, when
•
p W02
f
l
, it will be
focus
Fundamentals of Photonics
2017/5/24
57
CHAPTER 1---- Optical Resonator
In laser scanning, laser printing, and laser fusion, it is desirable to generate the
smallest possible spot size, this may be achieved by use of the shortest
possible wavelength, the thickest incident beam, and the shortest focal length.
Since the lens should intercept the incident beam, its diameter D must be at
least 2W0. Assuming that D = 2Wo, the diameter of the focused spot is given by
2W0 '
4
p
l F#
F#
f
D
where F# is the F-number of the lens. A microscope objective with small
F-number is often used.
Fundamentals of Photonics
2017/5/24
58
CHAPTER 1---- Optical Resonator
Beam collimate
locations of the waists of the incident and transmitted beams, z and z’ are
z'
z / f -1
-1
f
( z / f - 1) 2 ( z0 / f ) 2
The beam is collimated by making the location of the new waist z’ as
distant as possible from the lens. This is achieved by using the
smallest ratio z0/f (short depth of focus and long focal length).
Fundamentals of Photonics
2017/5/24
59
CHAPTER 1---- Optical Resonator
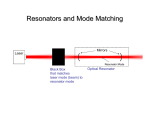
Beam expanding
A Gaussian beam is expanded and collimated using two
lenses of focal lengths f1 and f2,
Assuming that f1<< z and z - f1>> z0, determine the optimal
distance d between the lenses such that the distance z’ to the
waist of the final beam is as large as possible.
overall magnification M = W0’/Wo
Fundamentals of Photonics
2017/5/24
60
CHAPTER 1---- Optical Resonator
C). Reflection from a Spherical Mirror
Reflection of a Gaussian beam of curvature R1 from a mirror of curvature R:
W2 W1
1
1 2
f = -R/2.
R2 R1 R
R > 0 for convex mirrors and R < 0 for concave mirrors,
Fundamentals of Photonics
2017/5/24
61
CHAPTER 1---- Optical Resonator
R
R1
R1 - R
If the mirror is planar, i.e., R =∞, then R2= R1, so that the mirror reverses the
direction of the beam without altering its curvature
If R1= ∞, i.e., the beam waist lies on the mirror, then R2= R/2. If the mirror is
concave (R < 0), R2 < 0, so that the reflected beam acquires a negative
curvature and the wavefronts converge. The mirror then focuses the beam to a
smaller spot size.
If R1= -R, i.e., the incident beam has the same curvature as the mirror, then R2=
R. The wavefronts of both the incident and reflected waves coincide with the
mirror and the wave retraces its path. This is expected since the wavefront
normals are also normal to the mirror, so that the mirror reflects the wave back
onto itself. the mirror is concave (R < 0); the incident wave is diverging (R1 > 0)
and the reflected wave is converging (R2< 0).
Fundamentals of Photonics
2017/5/24
62
CHAPTER 1---- Optical Resonator
d). Transmission Through an Arbitrary Optical
System
An optical system is completely characterized by the matrix M of
elements (A, B, C, D) ray-transfer matrix relating the position and
inclination of the transmitted ray to those of the incident ray
The q-parameters, q1 and q2, of the incident and transmitted
Gaussian beams at the input and output planes of a par-axial optical
system described by the (A, B, C, D) matrix are related by
Fundamentals of Photonics
2017/5/24
63
CHAPTER 1---- Optical Resonator
ABCD law
The q-parameters, q1 and q2, of the incident and transmitted
Gaussian beams at the input and output planes of a par-axial optical
system described by the (A, B, C, D) matrix are related by
q2
Aq1 B
Cq1 D
Because the q parameter identifies the width W and curvature R of the
Gaussian beam, this simple law, called the ABCD law
Invariance of the ABCD Law to Cascading
If the ABCD law is applicable to each of two optical systems with
matrices Mi =(Ai, Bi, Ci, Di), i = 1,2,…, it must also apply to a system
comprising their cascade (a system with matrix M = M1M2).
Fundamentals of Photonics
2017/5/24
64
CHAPTER 1---- Optical Resonator
C. HERMITE - GAUSSIAN BEAMS
The self-reproducing waves exist in the resonator, and resonating inside of
spherical mirrors, plan mirror or some other form paraboloidal wavefront mirror,
are called the modes of the resonator
Hermite - Gaussian Beam Complex Amplitude
W0
2x
2y
x2 y 2
U l ,m ( x, y, z ) Al ,m [
]Gl [
]Gm [
] exp[- jkz - jk
j (l m 1) ( z )]
W ( z)
W ( z)
W ( z)
2 R( z )
-u 2
),
where Gl (u ) H l (u ) exp(
2
l 0,1, 2,...,
is known as the Hermite-Gaussian function of order l, and Al,m is a constant
Hermite-Gaussian beam of order (I, m). The Hermite-Gaussian
beam of order (0, 0) is the Gaussian beam.
Fundamentals of Photonics
2017/5/24
65
CHAPTER 1---- Optical Resonator
H0(u) = 1, the Hermite-Gaussian function of order O, the Gaussian function.
G1(u) = 2u exp( -u2/2) is an odd function,
G2(u) = (4u2 - 2) exp( -u2/2) is even,
G3(u) = (8u3 - 12u)exp( -u2/2) is odd,
Fundamentals of Photonics
2017/5/24
66
CHAPTER 1---- Optical Resonator
Intensity Distribution
The optical intensity of the (I, m) Hermite-Gaussian beam is
I l ,m ( x, y, z ) Al ,m
Fundamentals of Photonics
2
W0 2 2 2 x 2 2 y
[
] Gl [
]Gm [
]
W ( z)
W ( z)
W ( z)
2017/5/24
67
CHAPTER 1---- Optical Resonator
C. Gaussian Modes
•
Gaussian beams are modes of the spherical-mirror resonator;
Gaussian beams provide solutions of the Helmholtz equation under
the boundary conditions imposed by the spherical-mirror resonator
Beam
radius
z
a Gaussian beam is a circularly symmetric wave whose energy is confined
about its axis (the z axis) and whose wavefront normals are paraxial rays
Fundamentals of Photonics
2017/5/24
68
CHAPTER 1---- Optical Resonator
2
Gaussian beam intensity: I I W0 e
0
W ( z )
The Rayleigh range z0
2
2
2( x 2 y 2 ) - i k z x y -tg -1 z
2 R
z0
W 2 (z)
e
p W02
z0
l
where z0 is the distance called Rayleigh range, at which the beam
wavefronts are most curved or we usually called confocal prrameter
Beam width
W ( z ) W0 [1 (
z 2 1/ 2
) ]
z0
minimum value W0 at the beam waist (z = 0).
The radius of curvature
z02
R( z ) z
z
z 2
z z0
z0 2
R R( z ) z 1 z0 z
z
z0
z0 z
Beam waist
Fundamentals of Photonics
W0
l z0
p
2017/5/24
69
CHAPTER 1---- Optical Resonator
Gaussian Mode of a Symmetrical SphericalMirror Resonator
z2 z1 d
d
R1
z02
R1 z1
z1 2
R2
z0
- R2 z2
z2
z1
z1
0
Fundamentals of Photonics
-d ( R2 d )
, z2 z1 d
R2 R1 2d
z2 z z 2 -d ( R1 d )( R2 d )( R2 R1 2d )
0
2
( R2 R1 2d )
2017/5/24
70
CHAPTER 1---- Optical Resonator
the beam radii at the mirrors
Wi W0 [1 (
zi 2 1/ 2
) ] , i 1, 2.
z0
An imaginary value of z0 signifies that the Gaussian beam is in fact a
paraboloidal wave, which is an unconfined solution, so that z0 must be
real. it is not difficult to show that the condition z02 > 0 is equivalent to
0 (1
Fundamentals of Photonics
d
d
)(1 ) 1
R1
R2
2017/5/24
71
CHAPTER 1---- Optical Resonator
Gaussian Mode of a Symmetrical SphericalMirror Resonator
Symmetrical resonators with concave mirrors that is R1 = R2= -/RI
so that z1 = -d/2, z2 = d/2. Thus the beam center lies at the center
R
d
z0 (2 - 1)1/ 2
2 d
ld R
W
(2 - 1)1/ 2
2p
d
2
0
W12 W22
ld / p
{(d / R )[2 - (d / R )]}1/ 2
The confinement condition becomes
0
Fundamentals of Photonics
d
2
R
2017/5/24
72
CHAPTER 1---- Optical Resonator
Given a resonator of fixed mirror separation d, we now examine the
effect of increasing mirror curvature (increasing d/lRI) on the beam
radius at the waist W0, and at the mirrors Wl = W2.
As d/lRI increases, W0 decreases
until it vanishes for the concentric
resonator (d/lR| = 2); at this point
W1 = W2 = ∞
The radius of the beam at the
mirrors has its minimum value, WI =
W2= (ld/p)1/2, when d/lRI = 1
d
z0
2
Fundamentals of Photonics
W0 (
l d 1/ 2
)
W1 W2 2W0
2p
2017/5/24
73
CHAPTER 1---- Optical Resonator
C. Resonance Frequencies
The phase of a Gaussian beam,
( x, y, z ) kz - tg ( z
-1
k ( x2 y 2 )
)
z0
2 R( z )
At the locations of the mirrors z1 and z2 on the optical axia (x2+y2=0), we have,
(0, z2 ) - (0, z1 ) k ( z2 - z1 ) - [ ( z2 ) - ( z1 )] kd -
where
z
z0
( z ) tg -1
As the traveling wave completes a round trip between the two
mirrors, therefore, its phase changes by
2kz - 2
For the resonance, the phase must be in condition 2kz - 2 2qp ,
q 1, 2,3...
If we consider the plane wave resonance frequency
k 2p
We have q q F
F
p
Fundamentals of Photonics
2017/5/24
c
and
F c 2d
74
CHAPTER 1---- Optical Resonator
Spherical-Mirror Resonator Resonance Frequencies (Gaussian Modes)
q q F
F
p
1. The frequency spacing of adjacent modes is VF = c/2d, which is the same
result as that obtained for the planar-mirror resonator.
2. For spherical-mirror resonators, this frequency spacing is independent of
the curvatures of the mirrors.
3. The second term in the fomula, which does depend on the mirror curvatures,
simply represents a displacement of all resonance frequencies.
Fundamentals of Photonics
2017/5/24
75
CHAPTER 1---- Optical Resonator
D. Hermite - Gaussian Modes
The resolution for Helmholtz equation An entire family of solutions, the
Hermite-Gaussian family, exists. Although a Hermite-Gaussian beam of order
(I, m) has the same wavefronts as a Gaussian beam, its amplitude distribution
differs . It follows that the entire family of Hermite-Gaussian beams represents
modes of the spherical-mirror resonator
W0
2x
2y
x2 y 2
U l ,m ( x, y, z ) Al ,m [
]Gl [
]Gm [
] exp[- jkz - jk
j (l m 1) ( z )]
W ( z)
W ( z)
W ( z)
2 R( z )
(0, z ) kz - (l m 1) ( z )
2kd - 2(l m 1) 2p q, q 0, 1, 2,...,
Spherical mirror resonator Resonance Frequencies
(Hermite -Gaussian Modes)
l ,m,q q F (l m 1)
Fundamentals of Photonics
2017/5/24
p
F
76
CHAPTER 1---- Optical Resonator
longitudinal or axial modes: different q and same indices (l, m) the
intensity will be the same
transverse modes: The indices (I, m) label different means different
spatial intensity dependences
l ,m,q q F (l m 1)
p
F
Longitudinal modes corresponding to a given transverse mode (I, m) have resonance
frequencies spaced by vF = c/2d, i.e., vI,m,q – vI’,m’,q = vF.
Transverse modes, for which the sum of the indices l+ m is the same, have the same
resonance frequencies.
Two transverse modes (I, m), (I’, m’) corresponding mode q frequencies spaced
l ,m,q - l ',m ',q [(l m) - (l ' m ')]
Fundamentals of Photonics
2017/5/24
p
F
77
CHAPTER 1---- Optical Resonator
*E. Finite Apertures and Diffraction Loss
Since the resonator mirrors are of finite extent, a portion of the optical power escapes
from the resonator on each pass. An estimate of the power loss may be determined by
calculating the fractional power of the beam that is not intercepted by the mirror. That is
the finite apertures effect and this effect will cause diffraction loss.
For example:
If the Gaussian beam with radius W and the mirror is circular with radius a and a= 2W, each time
there is a small fraction, exp( - 2a2/ W2) = 3.35 x10-4, of the beam power escapes on each pass.
Higher-order transverse modes suffer greater losses since they have greater spatial extent in
the transverse plane.
In the resonator, the mirror transmission and any aperture limitation will
induce loss
The aperture induce loss is due to diffraction loss, and the loss depend
mainly on the diameters of laser beam, the aperture place and its diameter
We can used Fresnel number N to represent the relation between the size
of light beam and the aperture, and use N to represent the loss of
resonator.
Fundamentals of Photonics
2017/5/24
78
CHAPTER 1---- Optical Resonator
Diffraction loss
The Fresnel number NF
a2
a2
a2
NF
d l 2 z l pW 2
Attention: the W here is the beam width in the mirror, a is the dia. of mirror
Physical meaning:the ratio of the accepting angle (a/d) (form
one mirror to the other of the resonator )to diffractive angle of
the beam (l/a) .
The higher Fresnel number corresponds to a smaller loss
Fundamentals of Photonics
2017/5/24
79
CHAPTER 1---- Optical Resonator
N is the maximum number of trip that light will propagate in side resonator
without escape.
1/N represent each round trip the ratio of diffraction loss to the total energy
Symmetric confocal resonator
a12
a22
NF
2
2
p W1 p W2
For general stable concave mirror resonator, the Fresnel number for two
mirrors are:
1
a12
a12 g1
N F1
[ (1 - g1 g 2 )]2
2
p W1
d l g2
NF 2
1
a22
a22 g 2
[ (1 - g1 g 2 )]2
2
p W2 d l g1
Fundamentals of Photonics
2017/5/24
80
CHAPTER 1---- Optical Resonator
Home work 2
•
•
•
•
The light from a Nd:YAG laser at wavelength 1.06 mm is a Gaussian beam of 1 W optical power and
beam divergence 2q0= 1 mrad. Determine the beam waist radius, the depth of focus, the maximum
intensity, and the intensity on the beam axis at a distance z = 100 cm from the beam waist.
Beam Focusing. An argon-ion laser produces a Gaussian beam of wavelength l = 488 nm and waist
radius w0 = 0.5 mm. Design a single-lens optical system for focusing the light to a spot of diameter
100 pm. What is the shortest focal-length lens that may be used?
Spot Size. A Gaussian beam of Rayleigh range z0 = 50 cm and wavelength l=488nm is converted
into a Gaussian beam of waist radius W0’ using a lens of focal length f = 5 cm at a distance z from its
waist. Write a computer program to plot W0’ as a function of z. Verify that in the limit z - f >>z0 , the
relations (as follows) hold; and in the limit z << z0 holds.
Beam Refraction. A Gaussian beam is incident from air (n = 1) into a medium with a planar boundary
and refractive index n = 1.5. The beam axis is normal to the boundary and the beam waist lies at the
boundary. Sketch the transmitted beam. If the angular divergence of the beam in air is 1 mrad, what
is the angular divergence in the medium?
W0 ' MW0 M M r
W0 '
f
z- f
W0
[1 ( z0 / f ) 2 ]1/ 2
Fundamentals of Photonics
2017/5/24
81
CHAPTER 1---- Optical Resonator
Resonance Frequencies of a Resonator with an Etalon. (a) Determine the
spacing between adjacent resonance frequencies in a resonator
constructed of two parallel planar mirrors separated by a distance d = 15
cm in air (n = 1).(b) A transparent plate of thickness d1= 2.5 cm and
refractive index n = 1.5 is placed inside the resonator and is tilted slightly to
prevent light reflected from the plate from reaching the mirrors. Determine
the spacing between the resonance frequencies of the resonator.
Mirrorless Resonators. Semiconductor lasers are often fabricated from
crystals whose surfaces are cleaved along crystal planes. These surfaces
act as reflectors and therefore serve as the resonator mirrors. Consider a
crystal with refractive index n = 3.6 placed in air (n = 1). The light reflects
between two parallel surfaces separated by the distance d = 0.2 mm.
Determine the spacing between resonance frequencies vF, the overall
distributed loss coefficient ar, the finesse F, and the spectral width dv.
Assume that the loss coefficient (as= 1 cm-1).
Fundamentals of Photonics
2017/5/24
82
CHAPTER 1---- Optical Resonator
b). Parameter q transform for thin lens
If put the original point at the waist of beam, the parameter q will be
1
1
l
-i
q( z ) R( z ) p W 2 ( z )
The real part is concern with wave
front R(z), the imaginary part is
corresponding to beam radii w(z)
For q0 is the value at R(0)→∞
q0 q(0)
ip W02
l
Finally we have:
pW02
q( z ) i
z q0 z
l
Fundamentals of Photonics
2017/5/24
83
CHAPTER 1---- Optical Resonator
Parameter q in the thin lens transform
W1 W2
1 1 1
R' R f
1 1 1
q' q f
q01 q(0)
ip W02
l
q1 q01 z
1
1 1
q2 q1 f
q1 q z1
q2 q '- z2
1 1 1
-
q1 q2 f
1
1
1
q '- z2 q z1 f
Fundamentals of Photonics
2017/5/24
84
CHAPTER 1---- Optical Resonator
continue
(1 q'
Real part
z2
zz
)q ( z1 z2 - 1 2 )
f
f
z
q
-( ) (1 - 1 )
f
f
f - z1 W012
2
f - z2 W02
z
z
(1 - 1 )q02 (1 - 2 )q01
f
f
p W012
q q01 i
l
p W022
'
q q02 i
l
Imaginary part
q01q02
z1 z2
z1 z2 f
f
W012
W
2
02
z1 2 pW01 2
) (
)
f
lf
z
(1 - 1 )
f
z2 f [1 ]
z1 2 pW01 2
(1 - ) (
)
f
lf
Fundamentals of Photonics
(1 -
2017/5/24
W0 '
p 2W012W022
z1
z
z
(
1
)
1
2
l2 f
f
W
[1 (p W 2 / l R ')2 ]1/ 2
85
CHAPTER 1---- Optical Resonator
Special cases
• when z1→∞, then z2=F when incident beam waist is
in the far infinite the outlet beam waist is located at
the focal plan
• when z1=f, then z2=F, the incident beam waist is in
the object focal plan, the outlet beam waist will be in
the imaging focal plan
•
p W012 z1
when l f 1 - f
2
Fundamentals of Photonics
1 1 1
, then
z1 z2 f
2017/5/24
86
CHAPTER 1---- Optical Resonator
,
Beam waist radius
W0 ' MW0
Waist location
( z '- f ) M 2 ( z - f )
Depth of focus
2 z0' M 2 (2 z0 )
Divergence
Magnification
Fundamentals of Photonics
2 0'
M
2 0
M
z0
Mr
r
(1 r 2 )1/ 2
z- f
2017/5/24
Mr
f
z- f
87