Download Chapter 11 Gillis & Jackson Descriptive Statistics PP

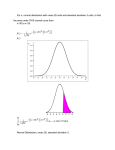
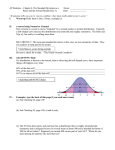
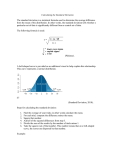
Chapter Eleven
A Primer for Descriptive
Statistics
Descriptive Statistics
• A variety of tools, conventions, and
procedures for describing variables
and relationships between variables
Measurement is the process of
assigning numbers to phenomena
according to a set of rules
Levels of Measurement
Nominal: involves no underlying continuum;
assignment of numeric values arbitrary
Examples: religious affiliation, gender, etc.
Levels of Measurement
Ordinal: implies an underlying continuum;
values are ordered but intervals are not
equal.
Examples: Community size, Likert items,
etc.
Levels of Measurement Cont.
Ratio: involves an underlying continuum;
numeric values assigned reflect equal
intervals; zero point aligned with true zero.
Examples: weight, age in years, % minority
Data Distributions
• A listing of all the values for any one variable
• The most basic technique for presenting a large
data set is to create a frequency distribution
table
• A systematic listing of all the values on a
variable from the lowest to the highest with the
# of times (frequency) each value was observed
Normal Distribution
• A normal distribution roughly follows a
bell-shaped curve
• Bimodal distribution (2 peaks eg. male &
female body weight)
• Platykurtic distribution (flat & wide, great
deal of variability)
• Leptokurtic distribution (peaked, little
variability)
Measures of Central Tendency
• A single numeric value that summarizes the
data set in terms of its “average” value.
• Eg. the nurse researcher uses the value of
98.6 F or 37 C to describe the average adult
body temperature
Measures of Central Tendency
Mean: calculated by summing values and
dividing by number of cases
Median: caluculated by ordering a set of
values and then using the middle most
value (in cases of two middle values,
calculated the mean of the two values.
Mode: the most frequently occuring value.
Measures of Dispersion
Range: calculated by substracting lowest value
from the highest value in a set of values.
Standard Deviation: a measure reflecting the
average amount of deviation
in a set of values.
___________
_
sd =
 (X - X)²
N-1
Dispersion Cont.
Variance: this measure is simply the
standard deviation squared.
 (X - X)²
Variance = sd² =
N - 1
Standardizing Data
• To standardize data is to report
data in a way that comparisons
between units of different size may
be made
Standardizing Data
Proportions: represents the part of 1 that some
element represents. A so-called batting average
is actually a proportion because it represents:
BA =
Number of Hits
Number at Bats
Percentage: a proportion may be converted
to a percentage by multiplying by 100.
If a players batting “average” is .359 we could
convert that to a percentage by multiplying by
100. In this case, the percentage of time the
person gets a hit is 35.9%.
In short, a percentage represents how often
something happens per 100 times.
Percentage Change: a measure of how much
something has changed over a given time
period. Percentage change is:
Time 2 - Time 1 x 100
Time 1
Thus, if there were 25 nurses now compared
to 17 five years earlier, the percentage change
over the 5 year period would be:
((25 - 17)  17) x 100 = 47.1%
Rates: represent the frequency of something
for a standard sized unit. Divorce rates,
suicide rates, crime rates are examples. So if
we had 104 suicides in a population of
757,465 the suicide rate per 100,000 would
be calculated as follows:
SR =
104
x 100 = 13.73
757,465
I.e., there are 13.73 suicides per 100,000
Ratio: represents a comparison of one thing
to another. So if there are 200 suicides in the
U.S. and 57 per 100,000 in Canada, the
U.S./Canadian suicide ratio is:
US Suicide Rate
= 200 = 3.51
Candian Suicide Rate
57
Normal Distribution
Much data in the social and physical world
is “normally distributed”. If it is this means
that there will be a few low values, many
more clustered toward the middle, and a few
high values. Normal distributions are:
• symmetrical, bell-shaped curve
• mean, mode, and median will be similar
•2/3 of cases ± 1 standard deviation of mean
• 95.6 cases ± 2 standard deviations of mean
Normal Distribution Cont.
Z Scores
A Z score represents the distance, in standard
deviation units, of any value in a distribution.
The Z Score formula is as follows:
__
Z = X - X
sd
Exercise:
Suppose:
Subject
Case 1
Case 2
Case 3
Case 4
Income Mean = $72,000; SD = $18,000
Education Mean = 11 years; SD = 4 years
Income
80,000
70,000
91,000
56,000
Education
14
10
19
8
Calculation Case 1:
Case 1 Z (income) = 80,000 - 72,000 = .44
18,000
Case 1 Z (education) = 14 - 11 = .75
4
SES score Case 1 = .44 + .75 = 1.19
Areas Under the Normal Curve
• draw normal curve, include lines to
represent problem
• calculate Z score(s) for problem
• look up value in Table 11.14
• Solve problem, recall that .5 of cases fall
above the mean, .5 below
• convert proportion to percentage, if needed
Exercise:
Suppose you wished to know percentage of cases will fall above
$100,000 in a sample whose MEAN is $65,000 and the SD is $22,000
Show p. 370 of text
Z = 1.59
100,000 - 65,000 / 22,000
look up in Table 11.14, p 368 = .4441
.5000 - .4441 = .0559 (proportion)
x 100 = 5.6% (percentage)
Describing Relationships
Between Variables
1. Crosstabular Analysis:
used with a nominal dependent variable
we cross-classify the information to
show the relation between an independent
and a dependent variable a standard table
looks like the following:
Table 11.11 Plans to Attend University by Size of Home Community
=================================================================
Town up
Town over
University Rural
to 5,000
5,000
TOTAL
Plans? N
%
N
%
N
%
N
%
----------------------------------------------------------------Plans
69 52.3
44 48.9
102 73.9
215 59.7
No Plans 63 47.7
46 51.1
36 26.1
145 40.3
___ _____
___ _____
___ _____
___ _____
TOTAL 132 100.0
90 100.0
138 100.0
360 100.0
----------------------------------------------------------------If appropriate, test of significance values entered here.
Rules for Crosstabular Tables:
• in
table title, name dependent variable first
• place dependent variable on vertical axis
• place independent on horizontal plane
• use clear variable labels
• run % figures toward independent variable
• report % to one decimal point
• statistical data reported below table
• interpret by comparing % in categories
of the independent variable
2. Comparing Means
• used when dependent variable is ratio
• comparison to categories of independent
variable
• both t-test and ANOVA may be used
Presentation may be as follows:
Mean Heart Rate by Treatment Group
-----------------------------------------------------------Treatment Group
Mean Heart Rate
Number of Cases
-----------------------------------------------------------Touch Therapy
74.6
78
Routine Treatment
77.1
77
COMBINED MEAN
75.8
155
-----------------------------------------------------------If appropriate, test of significance values entered here.
For Example: F = 3.514 df = 2,153 p = >.05
t Test
• T-test is used to determine:
• if the differences in the means of two
groups are statistically significant
• with samples under 30
• when comparing 2 groups on a ratio level
dependent variable
Analysis of Variance (ANOVA)
• ANOVA is used when 3 or more groups means are
compared, or
• When the means for 2 or more groups are compared
at 2 or more points in time in a single analysis (e.g.,
a pre-post experimental design)
• Computes a ratio that compares 2 kinds of
variability-with-in group & between-groups
variability
3. Correlation
• used with ratio level variables
• interest in both the equation and the strength
of the correlation
• Y = a + bX is the general equation
• the r is the symbol used to report the
strength of the correlation: can vary from
-1.0 to + 1.0
Sample Data Set
(X)
(Y)
2
3
3
4
5
4
7
6
8
8
Y
•
8
7
•
6
5
4
3
•
• •
2
1
0
0 1 2 3 4 5 6 7 8
X
Y
•
8
7
•
6
5
4
3
•
• •
Regression Line
2
1
0
0 1 2 3 4 5 6 7 8
X
Y
•
8
7
•
6
5
4
3
•
• •
b
h
b value (slope)
read here h/b
2
1
a value read here
0
0 1 2 3 4 5 6 7 8
X
Y
Predicted Value
8
7
•
6
5
4
3
•
•
• •
2
1
0
0 1 2 3 4 5 6 7 8
X