Download Solving Quadratic Equations

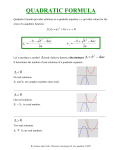
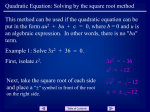
Using the Quadratic
Formula
Module VIII, Lesson 5
Algebra Online
VHS@PWCS
Cami Craig
Quadratic Review
1. A quadratic equation can have 3
different types of solutions. What are
they?
2. What is the solution to the following
quadratic equations?
a. x2 = 36
b. 2x2 = 8
c. x2 – 6 = -75
Click for the solutions.
Quadratic Review
1. A Quadratic can have:



1 solution
2 solutions
No solution
2. a. x = + 6
b. x = + 2
c. No solution
If you had
problems with
this review you
need to go back
to the last
lesson and look
over it again!
Solving quadratics of the form
ax2 + bx + c = 0
When quadratics are of this form, we can’t
solve for x by any of the methods that
have learned thus far.
b  b  4ac
x
2a
2
This can be sung to Pop Goes the Weasel! It
makes a neat way to remember it!
The quadratic formula can be used to
solve ANY Quadratic! IF you follow the
steps below!
1. Put the quadratic in standard
form.
ax2 + bx + c = 0
2. Identify a, b and c.
Try solving:
x2 + 5x + 4 = 0
1. It is already in standard form.
2. a = 1, b = 5 and c = 4
3.
3. Substitute a, b and c in the
2

5

5
 4(1)(4)
quadratic formula and simplify. x 
2(1)
2
b  b  4ac
x
Click to show steps for
2a
simplifying!
x2 + 5x + 4 = 0
5  52  4(1)(4)
x
2(1)
5  25  16
x
2
5  3
x
2
2
x
 1
2
5  9
x
2
From here we can
need to split what we
are simplifying to
account for the +.
5  3
x
2
8
x
 4
2
Try this one!
2x2 - 2x = 1
1. Put the quadratic in standard
form.
ax2 + bx + c = 0
2. Identify a, b and c.
3. Substitute a, b and c in the
quadratic formula and simplify.
b  b2  4ac
x
2a
1. 2x2 – 2x -1 = 1 – 1
2x2 – 2x – 1 = 0
2. a = 2, b = -2, c= -1
3.
(2)  (2)2  4(2)(1)
x
2(2)
Click to see how to
simplify
(2)  (2)2  4(2)(1)
x
2(2)
2 48
x
2(2)
x
2  12
4
x  1.37
2  12
x
4
From here you need to use a
calculator.
Make sure that you put
parentheses around the
numerator of each equation.
2  12
x
4
x  0.37
Try these on your own.
Click to check your answers.
1. 2x2 + 7x – 15 = 0
2. x2 – 2x – 15 = 0
3. -2x2 + 8x + 3 = 3
1. x = -5
x = 3/2
2. x = -3
x=5
3. x = 0
x=4