Download Honors Algebra 2 – Solving Quadratic Equations Practice Test

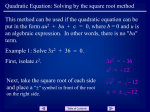
Algebra 2 Ch 5 Practice Test
Name ____________________________________
Date _____________
1. Solving Quadratic Equations
a. Find the roots of
16x2 + 64 = 0
b. Solve using any method
3(t – 7)2 = 540
c. Solve 6x2 – 7x – 5 = 0
d. Solve
by factoring.
e. To solve
by using the Square Root Property, you would first
rewrite the equation as _.
2. Simplifying
a. Simplify (x – 3)2
b. Simplify (2x – 4)(x2 – 2x + 5)
3. Simplifying Radicals
a.
45
b. 2 96
4. Complex Numbers
a. (9 – 3) / (2+3i)
b. Simplify (7 – 3i) – (5 + 2i)
c. Simplify (1 + 7i)( –2 + i)
d. The sum of 2 complex numbers is 8 – i. Given that one of the numbers is 11 – 3i,
what is the other number?
e. Simplify
.
5. Completing the Square
a. Complete the square to write in vertex form.State the vertex.y = x2 + 6x + 13
b. Find the value of c that makes x
10x c a perfect square.
c. The quadratic equation
is to be solved by completing the square.
What equation would be the first step in that solution?
6. Use the value of the discriminant to determine the number and type of roots for
each equation.
a.
b.
7. Quadratic Formula
a. Find the exact solutions to x2
8. Graphs of Quadratics
a. Find the y-intercept for f(x)
3x 1
0 by using the Quadratic Formula.
.
b. What is the equation of the axis of symmetry of
c. The graph of
?
opens ___ and has a ___ value.
d. The related graph of a quadratic equation is shown below. Use the graph to
determine the solutions of the equation.
i.
e. What is a quadratic equation that has roots 2 and 3?
f. What is the vertex of y 2(x
3)2 6?
g. What is the equation of the axis of symmetry of y
3(x
6)2 1?
h. Which quadratic function has its vertex at (2, 3) and passes through (1, 0)?
i. Find the x-intercepts and the y-intercept of the graph of y
2(x – 4)2
18.