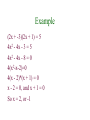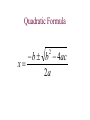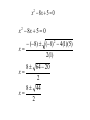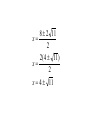* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Line (geometry) wikipedia , lookup
Elementary mathematics wikipedia , lookup
Recurrence relation wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Factorization wikipedia , lookup
Elementary algebra wikipedia , lookup
History of algebra wikipedia , lookup
Quadratic Equations P.7 Definition of a Quadratic Equation • A quadratic equation in x is an equation that can be written in the standard form • ax2 + bx + c = 0 • where a, b, and c are real numbers with a not equal to 0. A quadratic equation in x is also called a second-degree polynomial equation in x. The Zero-Product Principle If the product of two algebraic expressions is zero, then at least one of the factors is equal to zero. If AB = 0, then A = 0 or B = 0. Solving a Quadratic Equation by Factoring 1. If necessary, rewrite the equation in the form ax2 + bx + c = 0, moving all terms to one side, thereby obtaining zero on the other side. 2. Factor. 3. Apply the zero-product principle, setting each factor equal to zero. 4. Solve the equations in step 3. 5. Check the solutions in the original equation. Text Example • Solve 2x2 + 7x = 4 by factoring and then using the zero-product principle. Step 1 Move all terms to one side and obtain zero on the other side. Subtract 4 from both sides and write the equation in standard form. 2x2 + 7x - 4 = 4 - 4 2x2 + 7x - 4 = 0 Step 2 Factor. 2x2 + 7x - 4 = 0 (2x - 1)(x + 4) = 0 Solution cont. • Solve 2x2 + 7x = 4 by factoring and then using the zero-product principle. Steps 3 and 4 Set each factor equal to zero and solve each resulting equation. 2x-1=0 or x + 4 = 0 2x=1 x = -4 x = 1/2 Steps 5 check your solution Example (2x + -3)(2x + 1) = 5 4x2 - 4x - 3 = 5 4x2 - 4x - 8 = 0 4(x2-x-2)=0 4(x - 2)*(x + 1) = 0 x - 2 = 0, and x + 1 = 0 So x = 2, or -1 The Square Root Method If u is an algebraic expression and d is a positive real number, then u2 = d has exactly two solutions. If u2 = d, then u = d or u = -d Equivalently, If u2 = d then u = d Completing the Square If x2 + bx is a binomial then by adding (b/2) 2, which is the square of half the coefficient of x, a perfect square trinomial will result. That is, x2 + bx + (b/2)2 = (x + b/2)2 Text Example What term should be added to the binomial x2 + 8x so that it becomes a perfect square trinomial? Then write and factor the trinomial. The term that should be added is the square of half the coefficient of x. The coefficient of x is 8. Thus, (8/2)2 = 42. A perfect square trinomial is the result. x2 + 8x + 42 = x2 + 8x + 16 = (x + 4)2 x2 + 6x = 7 B divided by 2, squared x2 + 6x + 9 = 7 + 9 x + 3 2 = 16 x + 3 = 4 x = 4 - 3 x = 1, or - 7 Don’t forget to add to both sides Quadratic Formula - b b - 4ac x= 2a 2 x 2 - 8x + 5 = 0 x 2 - 8x + 5 = 0 - (-8) ( -8) 2 - 4(1)(5) x= 2(1) 8 64 - 20 x= 2 8 44 x= 2 8 2 11 x= 2 2( 4 11) x= 2 x = 4 11 The Discriminant and the Kinds of Solutions to ax2 + bx +c = 0 Discriminant b2 – 4ac Kinds of solutions to ax2 + bx + c = 0 b2 – 4ac > 0 Two unequal real solutions Graph of y = ax2 + bx + c Two x-intercepts b2 – 4ac = 0 One real solution (a repeated solution) One x-intercept b2 – 4ac < 0 No real solution; two complex imaginary solutions No x-intercepts