* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Interpret the Discriminant (10
Survey
Document related concepts
Transcript
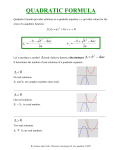
Interpret the Discriminant (10.7) To Solve Quadratic Equations in the form ax2 + bx + c = 0, where b 0 we can use the Quadratic Formula: b b 4ac 2a 2 x **Note: Be sure to put the equation in standard form first: ax2 + bx + c = 0 The b2 – (4ac) is called the discriminant The value of the discriminant can be used to determine the number of solutions We learned that a quadratic equation can have a different number of solutions: 2 Solutions 2 points of intersection 1 Solution 1 point of intersection No Solution No point of intersection b2 – (4ac) is Positive Number b2 – (4ac) is 0 b2 – (4ac) is Negative Number 1 Tell whether the equation has two solutions, one solution, or no solution. Ex. 2x2 + 6x + 5 = 0 a = _____ b = _____ c = _____ b2 – (4ac) = _______________________ = ______ number of solutions: __________________ Ex. x2 + 4x + 3 = 0 a = _____ b = _____ c = _____ b2 – (4ac) = _______________________ = ______ number of solutions: __________________ Ex. 4x2 – 12x + 9 = 0 a = _____ b = _____ c = _____ b2 – (4ac) = _______________________ = ______ number of solutions: __________________ Ex. 3x2 – 7 = 2x a = _____ b = _____ c = _____ b2 – (4ac) = _______________________ = ______ number of solutions: __________________ 2