Download Unit 3 Quantum Numbers PPT

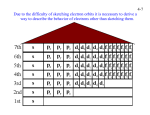
Light and Energy
In 1900 Max Planck helped us move
toward a better understanding of
electromagnetic radiation.
Matter can gain or lose energy only in small,
specific amounts called quanta.
A quantum is the minimum amount of energy
that can be gained or lost by an atom.
Atomic Emission Spectrum




Electrons gain energy and ‘jump’ to a higher
energy level.
This is an unstable excited state.
The electrons rele se energy when they return to
their ground state.
We see this energy as light.
The Bohr Quantum Model
The electron in a hydrogen
atom moves around the
nucleus only in certain
allowed circular orbits
Ground State: The lowest
possible energy level.
Excited State: Higher
energy level.
Atomic Emission Spectra
Wave-Particle Duality Theory (Einstein)
Is energy a wave like light, or a particle?
 BOTH
Atomic Theory
Louis de Broglie (1892 – 1987)
•Matter has characteristics of both waves and
particles
•Electrons move in wavelike motion in the
•circular orbits
Heisenberg Uncertainty Principle
There
is a fundamental limitation
to just how precisely we can know
both the position and momentum of
a particle at a given time
Schrodinger



Came up with an equation to describe the
probability of finding an electron within a 3D
area of space.
These equations are called wavefunctions. The
wavefunctions describe orbitals.
Orbitals are the building block of electron
arrangement.
Quantum Numbers
At the conclusion of our time
together, you should be able to:
 List and define each of the 4
quantum numbers.
 Relate these numbers to the state,
city, street and home address for the
electron.
 Give the maximum number of
electrons for each level and sublevel.
 Draw the basic shape of the 4
sublevels.
Quantum Numbers

The location of an electron is described with 4
terms or the 4 quantum numbers.
- Energy Level = n
- Sublevel = l
- Orbital = ml
- Spin = ms
Principal Quantum Number - n
Symbol = n
 Represents the main energy level of the electron
and its distance from the nucleus
 Equation: 2n2 - shows how many electrons can
be in each energy level
(e.g. 3rd energy level: 2(3)2 = 18 total possible ein this energy level)
Your turn: How many electrons in the 4th energy
level?
32

Principal Quantum Number - n

In an address analogy, this would be the state in
which the electron would probably be found.
Presently, we can find electrons in 7 states.

Values are 1-7
The Second Quantum Number - l



This number describes sublevels, shapes of
these sublevels and is the Angular momentum
quantum number.
The first 4 sublevels are named s, p, d, f.
Each sublevel has a unique number of orbitals
and shape:
Shape of the “s” Sublevel
• s for "Sphere": the simplest shape, or shape of the
simplest atoms like hydrogen and helium
• Contains 1 orbital.
Shapes of the “p” Sublevel
• p for "Peanut/Petal": a more complex shape that
occurs at energy levels 2 and above
• Contains 3 orbitals.
Shapes of the “d” Sublevel
• d for "Double Peanut/Petal": a complex shape
occurring at energy levels 3 and above
• Contains 5 orbitals.
Shapes of the “f” Sublevel
• f for "Flower": bizarre-shaped orbitals for
electrons of very large atoms
• Contains 7 orbitals.
The Second Quantum Number - l

In the address analogy, this would be the city in
which the electron would probably be found. In
the first state there would be 1 city, in the
second state there would be 2 cities...
The Second Quantum Number - l



The 2nd Quantum Number = 0 to (n-1)
Gives the sublevel type the electron is found in:
s, p, d, or f.
Therefore:
 For s, l = 0
 For p, l = 1
 For d, l = 2
 For f, l = 3
n=1
n=2
n=3
n=4
l=0
l = 0, 1
l = 0, 1, 2
l = 0, 1, 2, 3
designated by letters
l = 0 s orbital
l = 1 p orbital
l = 2 d orbital
l = 3 f orbital
s
p
n=1
n=2
n=3
n=4
n=5
n=6
n=7
d
f
The Third Quantum Number - m






This number describes the specific orbital that
an electron is in on a specific sublevel.
Value = –l to 0 to +l
s has one orbital,
p has three orbitals,
d has five orbitals and
f has 7 orbitals.
The Third Quantum Number - m
For s, l = 0; For p, l = 1; For d, l = 2; For f, l = 3






Values for m:
s = ___
p = ___ ___ ___
0
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
f = ___ ___ ___ ___ ___ ___ ___
-3 -2 -1
0 1
2
3
The Fourth Quantum Number - s






This number describes the spin of the electrons
in an orbital. There can be two electrons in each
orbital as long as they are spinning in opposite
directions.
In the address analogy, this would be
the house number of the electron.
There can only be 2 houses on each
street
Values are +1/2 = clockwise spin
-1/2 = counter clockwise spin
Values for s:


s = (-1/2, +1/2)
Each orbital can hold
only two oppositely
spinning electrons,
so there are only two
possible “s” values
+1/2
-1/2
Quantum Numbers
Let’s see if you can:
 List and define each of the 4
quantum numbers.
 Relate these numbers to the state,
city, street and home address for the
electron.
 Give the maximum number of
electrons for each level and sublevel.
 Draw the basic shape of the 4
sublevels.
1 s orbital
3 p orbitals
5 d orbitals
each orbital holds 2e-4th quantum numberms spin

7 f orbitals
s
p
n=1
n=2
n=3
n=4
n=5
n=6
n=7
d
f
5p
4d
What are the
quantum numbers for
this electron?
n=
5s
4p
3d
4s
4
3p
L=
1
3s
2p
m = +1
s=
-1/2
2s
Usually quantum
numbers are
expressed like this:
1s
(4, 1, +1, -1/2)
5p
4d
What are the
quantum numbers for
this electron?
5s
4p
3d
4s
n=
L=
3
2
m = -1
s = +1/2
3p
3s
2p
2s
1s
(3, 2, -1, +1/2)
5p
4d
5s
Which electron
has this set of
quantum
numbers?
(2, 0, 0, -1/2)
4p
4s
3p
3s
2p
2s
1s
3d
5p
4d
5s
Which electron
has this set of
quantum
numbers?
(3, 1, -1, -1/2)
4p
4s
3p
3s
2p
2s
1s
3d
How do we know when an electron has
moved from an excited state to the
ground state? The electron will
1.
2.
3.
4.
5.
Release a photon.
Release a specific amount of
energy.
Release a specific color.
Release a quantum of energy.
All of the above are correct.
What does the second quantum number (l)
describe?
1.
2.
3.
4.
Orbital shape.
Energy level.
Electron spin.
Orbital orientation.
Which quantum number has values of +½
or –½?
1.
2.
3.
4.
Orbital shape.
Energy level.
Electron spin.
Orbital orientation.
Which of the following is not a possible
orbital shape?
1.
2.
3.
4.
s
p
z
f
What is currently the highest possible
principal quantum number an electron can
have?
1.
2.
3.
4.
No limit
5
6
7
How many electrons will the 4th energy
level hold?
1.
2.
3.
4.
5.
No limit
8
18
32
50
The p sublevel would look like a
1.
2.
3.
4.
5.
sphere
petal
double petal
flower
mess
Quantum Numbers
At the conclusion of our time
together, you should be able to:
 Continue to relate Quantum
Numbers to the state, city, street and
home address for the electron.
 Give the 4 quantum number for every
electron of every atom on the periodic
table.
Let’s Try Helium




H is 1s1
He has 2 electrons, can we add another electron
spinning in the other direction in the first energy
level of the s sublevel with its 1 spherical orbital?
Yes, He is 1s2
He has 2 electrons spinning in opposite
directions in the s sublevel with its spherical
shape with 1 orientation.
Remember the Quantum # Summary for
Hydrogen




1s1
Hydrogen has one electron spinning in a
clockwise direction in the first energy level that
has one spherical orbital in its s sublevel.
The 4 quantum numbers for H are:
1, 0, 0, +1/2
The Pauli Exclusion Principle



No two electrons in an atom can have the same
set of four quantum numbers.
Therefore, the second electron that He has must
have a different set of 4 Quantum Numbers.
What would they be??
The 4 Quantum Numbers of Helium
n
1
l
0
m
0
s
-1/2
The 4 Quantum Numbers of Helium






No two electrons in an atom can have the same
set of four quantum numbers.
What principle??
Pauli Exclusion Principle
Therefore, the second electron that He has must
have a different set of 4 Quantum Numbers.
What would they be??
1, 0, 0, -1/2
Let’s Try Lithium



He is 1s2
He has 2 electrons, can we add
another electron spinning in
another direction in the first
energy level of the s sublevel with
its 1 spherical orbital?
No, the third electron must go to
the 2nd energy level which has 2
sublevels, s and p, s with its one
spherical orbital and p with its 3
orientations of its petal shaped
orbitals.
Let’s Try Lithium




So the address for all 3 electrons
of Li is:
1s2 2s1
This is called the electron
configuration for Li and basically
says that the first two electrons of
Li are in the s sublevel with its
one spherical shape with the 3rd
electron in the 2 energy level, s
sublevel with its bigger spherical
shape.
The Quantum #’s of the 3rd
electron:
The 4 Quantum Numbers for the 3rd
Electron of Lithium
n
2
l
0
m
0
s
+1/2
Now Beryllium:





Add one more electron to Li :
1s2 2s1? Where would it go??
1s2 2s2
The 2s sublevel with its one
spherical orbital can hold 2
electrons spinning in opposite
directions.
The Quantum #’s of the 4th
electron:
The 4 Quantum Numbers for the 4th
Electron of Beryllium
n
2
l
0
m
0
s
-1/2
What About Boron:







Add one more electron to Be:
1s2 2s2? Where would it go??
1s2 2s3 ?
No
1s2 2s2 2p1
The 2s sublevel with its one
spherical orbital is full. We must
now start filling the 2p sublevel
with its 3 orbitals
The Quantum #’s of the 5th
electron:
The Electrons of the 2nd Energy Level for
Boron


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 5th
Electron of Boron
n
2
l
1
m
-1
s
+1/2
Let’s Move to Carbon:




Add one more electron to B:
1s2 2s2 2p2
The 2p sublevel has 3 orbitals.
However, we can’t put another
electron in the first orbital of p.
Why?
Hund’s Rule: Orbitals of equal
energy are each occupied by one
electron before any orbital is
occupied by a second electron.
The Electrons of the 2nd Energy Level for
Carbon


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 6th
Electron of Carbon
n
2
l
1
m
0
s
+1/2
Nitrogen:




Add one more electron to C:
1s2 2s2 2p3
The 3rd electron in the p sublevel
must go into the 3rd orbital.
Why?
Again Hund’s Rule: Orbitals of
equal energy are each occupied
by one electron before any orbital
is occupied by a second electron.
The Electrons of the 2nd Energy Level for
Carbon


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 7th
Electron of Nitrogen
n
2
l
1
m
1
s
+1/2
Oxygen:



Add one more electron to N:
1s2 2s2 2p4
The 4th electron in the p sublevel
must begin to double up the
electrons of the three p orbitals.
The Electrons of the 2nd Energy Level for
Carbon


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 8th
Electron of Oxygen
n
2
l
1
m
-1
s
-1/2
Fluorine:



Add one more electron to O:
1s2 2s2 2p5
Where would the 5th electron for
the 2p orbitals go?
The Electrons of the 2nd Energy Level for
Fluorine


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 9th
Electron of Fluorine
n
2
l
1
m
0
s
-1/2
Neon:



Add one more electron to F:
1s2 2s2 2p6
Where would the 6th electron for
the 2p orbitals go?
The Electrons of the 2nd Energy Level for
Neon


s = ___
0
p = ___ ___ ___
-1
0 +1
The 4 Quantum Numbers for the 10th
Electron of Neon
n
2
l
1
m
1
s
-1/2
What About Sodium:

Add one more electron to Ne:

1s2 2s2 2p7 No!!
The 2p sublevel with its 3 orbitals
is full. We must now go to the 3rd
energy level with its 3 sublevels,
s, p, and d, and start filling
electrons all over again!

The Electrons of the 3rd Energy Level for
Sodium




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the 11th
Electron of Sodium
n
3
l
0
m
0
s
+1/2
What About Magnesium:

Add one more electron to Na:

1s2 2s2 2p6 3s2
Remember, the s sublevel with its
one spherical orbital can have
one more electron.

The Electrons of the 3rd Energy Level for
Magnesium




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the 12th
Electron of Magnesium
n
3
l
0
m
0
s
-1/2
Aluminum:

Add one more electron to
Mg:

1s2 2s2 2p6 3s2 3p1
Remember, the s sublevel
with its one spherical orbital
can only have 2 electrons.
The next electron must start
to fill the 3p sublevel with its
3 orbitals.

The Electrons of the 3rd Energy Level for
Aluminum




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the 13th
Electron of Aluminum
n
3
l
1
m
-1
s
+1/2
Silicon to Argon:

Keep adding one more
electron to Al:

1s2 2s2 2p6 3s2 3p2-6
Remember Hund’s rule. We
will put one electron in each
of the p orbitals and then
come back to double up.

The Electrons of the 3rd Energy Level for
Silicon to Argon




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the 18th
Electron of Argon
n
3
l
1
m
1
s
-1/2
Quantum Numbers
Let’s see if you can:
 Continue to relate Quantum
Numbers to the state, city, street and
home address for the electron.
 Give the 4 quantum number for every
electron of every atom on the periodic
table.
The 5f sublevel with its orbitals would
look like a
1.
2.
3.
4.
5.
sphere
petal
double petal
flower
mess
How many orbitals are in the 5f sublevel?
1.
2.
3.
4.
5.
No limit
1
3
5
7
How many electrons will the 4f sublevel
hold?
1.
2.
3.
4.
5.
2
6
10
14
18
In the address analogy, the first quantum
number is the state and the second
quantum number is the city. How many
cities are there in the second state?
1.
2.
3.
4.
5.
1
2
3
4
5
In the address analogy, the second state
can have how many total streets?
1.
2.
3.
4.
5.
1
2
3
4
5
Quantum Numbers
At the conclusion of our time
together, you should be able to:
 Explain the Aufbau principle
and the diagonal rule.
 Use Hund’s rule in an orbital
filling diagram.
 Give the quantum numbers
for every electron of every
atom on the periodic table.
 Draw the electron
configuration and orbital
notation for every element.
Now Potassium:





We should now start to fill
the 3d sublevel with its 5
orbitals.
1s2 2s2 2p6 3s2 3p6 3d1
But now we must consider ???
the Aufbau Principle:
An electron will occupy the
lowest energy level orbital
that can receive it.
Look at the energy needed
for 3d vs. 4s:
The Aufbau Principle



You will need to remember this chart so that you
place electrons in the correct order.
An easy way to remember the filling order is to
follow the diagonal rule.
Check it out on the next slide:
Maybe You’ve Seen
This Chart???
1s
2s
2p
3s
3p
3d
4s
4p
4d
4f
5s
5p
5d
5f
5g?
6s
6p
6d
6f
6g?
6h?
7s
7p
7d
7f
7g?
7h?
7i?
It Represents the
Diagonal Rule
Steps:
1. Write the energy levels top to bottom.
2. Write the orbitals in s, p, d, f order. Write the
same number of orbitals as the energy level.
3. Draw diagonal lines from the top right to the
bottom left.
4. To get the correct order,
follow the arrows!
Diagonal Rule
1s
2s
2p
3s
3p
3d
4s
4p
4d
4f
5s
5p
5d
5f
5g?
6s
6p
6d
6f
6g?
6h?
7s
7p
7d
7f
7g?
7h?
By this point, we are
past the current
periodic table so we
can stop.
7i?
The Aufbau Principle



But there is even an easier way to remember the
filling order.
Have you noticed areas in the periodic table
where certain sublevels are filling??
Check it out on the next slide:
The 4 Blocks of the Periodic Table
The Aufbau Principle





So, what block is always filling on the left side of
the periodic table??
The s block!!
What period is it??
The 4th!!
Therefore, 4s will begin filling before we fill 3d!!!
So is Potassium?

1s2 2s2 2p6 3s2 3p6 3d1
No!!!

1s2 2s2 2p6 3s2 3p6 4s1

The Electrons of the 4rd Energy Level for
Potassium and Calcium




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the 20th
Electron of Calcium
n
4
l
0
m
0
s
-1/2
The “D” Block Electrons



The next electron for Scandium will now start to
fill the “D” block.
Please note that the energy level for the d
sublevel is not 4. We have not filled 3d yet.
Therefore, the “D” block will always be one
energy level behind the current energy level.
Remember the Shape of the “d” Orbitals
• d for "Double Peanut/Petal": complex shape
occurring at energy levels 3 and above
•How many orbitals (orientations) does “d” have?
•5
So for Scandium to Zinc


Following Hund’s Rule, we will put one electron
in each of the 3d orbitals before we begin to
double up the electrons in each orbital.
Remember that the “d” block is always one
energy level behind.
The Electrons of the 3rd Energy Level for
Scandium to Zinc




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the Circled
Electron of Zinc
n
3
l
2
m
1
s
+1/2
Gallium to Krypton





So, what block is always filling on the right side
of the periodic table??
The p block!!
What period is it??
Back to the 4th!!
Therefore, 4p will begin filling after we fill 3d!!!
The Electrons of the 4rd Energy Level for
Gallium to Krypton




s = ___
0
p = ___ ___ ___
-1
0 +1
d = ___ ___ ___ ___ ___
-2 -1 0
1
2
The 4 Quantum Numbers for the Circled
Electron of Krypton
n
4
l
1
m
-1
s
-1/2
Rubidium and Strontium





So, what block is always filling on the left side of
the periodic table??
The s block!!
What period is it??
5th!!
Remember, the 4th energy level has 4 sublevels,
s, p, d, and f. Because of the Aufbau Principle,
d and f will fill later.
Rubidium and Strontium


Let’s do the electron configuration for these two
elements
1s2 2s2 2p6 3s2 3p6 4s2

3d10

4p6

5s1

or

5s2
How About Yttrium to Cadmium?

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2

4d1-10
Indium to Xenon?

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10

5p1-6
Cesium and Barium?

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6
6s1-2

do the 4 quantum numbers for 55th
electron of Barium.
 Now
The 4 Quantum Numbers for the Circled
Electron (55th) of Barium
n
6
l
0
m
0
s
+1/2
The “F” Block Elements


Now we come to a confusing part of the periodic
table.
Note that element #57, Lanthanum, is in the “d”
block but the next element #58, Cerium, drops
down to the “f” block.
The Periodic Table
The “F” Block Elements

Also note that according to the Aufbau Principle,
after 6s should fill 4f and then 5d.
The “F” Block Elements


Recent discoveries suggest that Lanthanum is
not the first element of the 4f block as previously
thought, but really is the first element of the 5d
block.
From there we will move to the 4f block.
Lanthanum?

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1

Then Cerium is

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1

4f1
The Rest of the 4f Block
#58 Praseodymium to #71 Lutetium

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1

4f1-14
The Electrons of the 4f Sublevel






6s = ___
0
6p = ___ ___ ___
-1
0 +1
5d = ___ ___ ___ ___ ___
-2 -1
0
1
2
4f = ___ ___ ___ ___ ___ ___ ___
-3 -2 -1
0
1
2
3
The 4 Quantum Numbers for the Circled
Electron (67th) of Lutetium
n
4
l
3
m
-1
s
-1/2
Now Back to the “D” Block Elements



As we follow the numbers on the Periodic Table,
you will see that element #72, Hafnium, is back
in the “d” block.
Therefore, Hafnium’s configuration would be:
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14

5d2
 Right??
 Wrong!!
Now Back to the “D” Block Elements

Why? Count the total electrons…
73 not 72
Why? Because 5d2 includes 5d1
I’ve counted 5d1 twice!!
Therefore, I must do this

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2





5d1 4f14 5d2
The Rest of the “D” Block Elements

Tantalum to Mercury

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2

5d1 4f14 5d3-10
Now to the 6p Block Elements

Thallium to Radon

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14 5d10

6p1-6
What’s Next

#87 - #88, Francium and Radium

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14 5d10 6p1-6

7s1-2
Now We Run into the Crazy Area

#89, Actinium

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14 5d10 6p1-6 7s2

6d1
#90 - #103, Thorium to Lawrencium


1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14 5d10 6p1-6 7s2 6d1

5f1-14
Finally, We Finish Up in the D Block



#104 - #112, Rutherfordium to Copernicium
Don’t forget to cross out the 6d1 electron when
you come back to the “d” block
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2
 5d1 4f14 5d10 6p1-6 7s2 6d1 5f14

6d2-10
Quantum Numbers
Let’s see if you can:
 List and define the 4
principles that are part of
quantum numbers.
 List and define each of the 4
quantum numbers.
 Give the quantum number for
every electron of every atom
on the periodic table.
Your Turn

Let’s see if you can do the last 4 orbital filling
diagrams and the 4 quantum numbers for the
last electron of #112, Copernicium

1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2

5d1 4f14 5d10 6p1-6 7s2 6d1 5f14 6d10
The Electrons of the 4 Configurations for
Copernicium






7s = ___
0
6p = ___ ___ ___
-1
0 +1
6d = ___ ___ ___ ___ ___
-2 -1
0
1
2
5f = ___ ___ ___ ___ ___ ___ ___
-3 -2 -1
0
1
2
3
The 4 Quantum Numbers for the Circled
Electron (112th) of Copernicium
n
6
l
2
m
2
s
-1/2

It is impossible to determine both the position
and the momentum of an electron at the same
time.

An electron occupies the lowest energy level
available.

No two electrons in the same atom can have
the same set of four quantum numbers.

In other words, no two electrons can be in the
same place at the same time.

Orbitals of equal energy are each occupied by
ONE electron before any orbital is occupied by
a SECOND electron

All electrons in a single occupied orbital must
have the same spin.




Symbol = n
Represents the main energy level of the
electron
Range = 1- 7
Ex. = 3s2
Principal Quantum number = 3






Symbol = l (small letter L)
Represents the shape of the orbital (also called
sublevel)
Range = 0 – n-1 (whole number)
Shapes:
0 = s (sphere)
1 = p (petal)
2 = d (double petal)
3 = f (flower)
Ex. = 3s2
AM Quantum number = 0




Symbol = m
Represents the orientation of the orbital around
the nucleus
Each line holds 2 electrons
m = -l to +l; Therefore: s = 0, p = 3, d = 5…
___ = s
0
___ ___ ___ = p
-1
0
+1
___ ___ ___ ___ ___ = d
-2
-1
0
+1 +2
___ ___ ___ ___ ___ ___ ___ = f
-3
-2
-1
0
+1 +2 +3

Ex. = 3s2
Magnetic Quantum number = 0

2 Spin States
Clockwise spin
= +1/2 (upward
arrow)
 Counterclockwise spin
= -1/2 (downward
arrow)
A single orbital can hold two electrons, but they
must have opposite spins
 Ex. = 3s2
Spin Quantum number = -1/2

Congratulations!!!!

You can now do the complete electron
configurations, orbital notations and give 4
quantum numbers (addresses) for every
electron of every element on the periodic table!!!
GRADING SCALE
•
A = upright and taking air
•
B = eyes notable open
•
C = responding to the environment
•
D = comatose
•
F = decomposed