Download Number Patterns (Sequences)

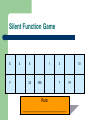
Number Patterns (Sequences)
We are learning to…analyze
patterns and predict numbers in
sequences.
Wednesday, May 24, 2017
Silent Function Game
X
Y
4
5
23
1
398
3
7
Rule:
__________________________
10
79
Vocabulary for Patterns and Sequences



Term - a number or object in a sequence
Linear Sequence – a pattern in which the
next term increases or decreases by the
same amount (constant rate of change)
Non-Linear Sequence – a pattern in which
the next term does not increase or decrease
by the same amount (varying rate of change)
Analyze the pattern: 2, 4, 6, 8, 10…



The pattern is linear, because it demonstrate
a constant rate of change.
The pattern starts at 2 and increases at a
constant rate of 2.
The next 5 terms of the pattern are:
…12, 14, 16, 18, 20.
Analyze the pattern: 2, 4, 6, 8, 10…



The pattern is linear, because it
demonstrates a constant rate of change.
The pattern starts at 2 and increases at a
constant rate of 2.
The next 5 terms of the pattern are:
2, 4, 6, 8, 10…12, 14, 16, 18, 20…
Analyze the pattern: 2, 5, 10, 17, 26…



The pattern is non-linear, because it does not
demonstrate a constant rate of change.
The pattern starts at 2 and increases by
consecutive odd numbers.
The next 5 terms of the pattern are:
2, 5, 10, 17, 26… 37, 50, 65, 82, 101…
Analyze the pattern: 1, 4, 7, 10, 13…



The pattern is linear, because it
demonstrates a constant rate of change.
The pattern starts at 1 and increases at a
constant rate of 3.
The next 5 terms of the pattern are:
1, 4, 7, 10, 13… 16, 19, 22, 25, 28…
Patterns and Functions
 Think
of a sequence as just
the outputs of a function.
Put the pattern 2, 4, 6, 8, 10… in the input/output table below.
X
Y
1
2
2
4
3
6
4
8
5
10
What is the function (numerical expression) that will model the
input/output table?
2x  y
_______________________
Use this function to predict the
25th term of the sequence.
2 x  y if x  25
2(25)  y
50  y
Use this function to predict the
52nd term of the sequence
2 x  y if x  52
2(52)  y
The 25th term of the sequence is 50!
The 52nd term of the sequence is 104!
104  y
Put the pattern 2, 5, 10, 17, 26 … in the input/output table below.
X
Y
1
2
2
5
3
10
4
17
5
26
What is the function (numerical expression) that will model the
input/output table?
x 1  y
2
_______________________
Use this function to predict the
15th term of the sequence.
x 2  1  y if x  15
152  1  y
225  1  y
226  y
Use this function to predict the
100th term of the sequence
x 2  1  y if x  100
1002  1  y
10, 000  1  y
10, 001  y
The 15th term of the sequence is 226! The 100th term of the sequence is 10,001!
Put the pattern 1, 4, 7, 10, 13… in the input/output table below.
X
Y
1
1
2
4
3
7
4
10
5
13
What is the function (numerical expression) that will model the
input/output table?
3x  2  y
_______________________
Use this function to predict the
250th term of the sequence.
3x  2  y if x  250
3(250)  2  y
750  2  y
748  y
Use this function to predict the
1000th term of the sequence
3x  2  y if x  1000
3(1000)  2  y
3000  2  y
2998  y
The 250th term of the sequence is 748!
The 1000th term of the sequence is 2998!
Assessment
Analyze the pattern:
7, 12, 17, 22, 27…