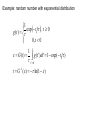Download Document

Pseudo-random-number
generators
Random numbers: the numbers generated by a
stochastic process
•They are indispensible in any simulations based on
radom sampling.
•The „true” random numbers are obtained by
hardware devices (the so-called random-noise
generators). These are, however, expensive.
•However, by performing a sequence of algebraic
operations on integer numbers, a sequence of
numbers can be generated which are effectively
random. Such numbers are referred to as pseudorandom numbers.
Linear Congruential Generators (LCG)
x j 1  ax j  c mod m
A sequence of pseudo-random numbers generated by
LCG has a period m, if and only if:
(a) c and m do not have common divisors.
(b) b=a-1 is a multiplicity of any primary number p,
which is a divisor of m.
(c) b is a multiplicity of 4, if m also is a multiplicity of
4.
The sequences of consecutive t pseudo-random
numbers generated by MLCG form a regular tdimensional lattice.
Example: t=2
xi+1
m=7, a=3
xi
The uniform feature of the pseudo-random number
distribution depends very strongly on the ratio of m do a
m=97, a=23
ui+1
ui+1
m=97, a=29
ui
xi
ui 
m
ui
Conditions for uniformity
dt – the largest distance between lattice nodes
dt  m

1
t
d t  m
Almost uniform distribution

1
t
d t  d t*  ct m
4
c2   
3

1
4
 64 
c6   
 3 


1
t
Significant deviation from the uniform
distribution
Lower limits on the distance
c3  2
1
12
c7  2

1
6

3
7

1
4

1
2
c4  2
c8  2
c5  2

3
10
Spectral test
d m
St m, a  
 0.65
d t m, a 
*
t
Appropriate values of the modules m and multipliers a for
transferable generators with the 32- and 16-bit arithmetics
32 bit
16 bit
m
2147483647
2147483563
a
39373
40014
m
32749
32363
a
162
157
2147483399
2147482811
2147482801
40692
41546
42024
32143
32119
31727
160
172
146
2147483739
45742
31657
142
ui+1
m=32749, a=162
ui
Multiplicative linear congruent
generators (MLCG)
x j 1  ax j mod m
Faster than te LCG generators but have a shorter period the
number 0 cannot be obtained.
The rank of an MLCG generator: the smallest l that satisfies the
equation
al mod m = 1
The maximum period of a pseudo-random numbers generated
by an MLCG is equal to the rank of that generator.
A portable version of MLCG designed by
Wichmann, Hill, and L’Ecuyer
a2  m
q  m div a, r  m mod a
m  aq  r
[ax] mod m  [ax  ( x div q )m] mod m
 [ax  ( x div q)( aq  r )] mod m
 [a{x  ( x div q )q}  ( x div q )r ] mod m
 [a ( x mod q )  ( x div q )r ] mod m
K=IX/IQ
IX=IA*(IX-K*IQ)-K*IR
IF (IX.LT.0) IX=IX+M
M=2147483563 IA=40014 IQ=53668 IR=12211
Best results are obtained if several MLCG generators are combined.
The VRND generator (based on the XOR operation) and RANDOMV
(LCG).
The ran0, ran1 (shortest execution time), ran2 (optimally randomized
numbers), ran3 (MLCG) generators from Numerical Recipes
Generation of real pseudo-random numbers
IEOR: bitwise exclusive OR
A
1
0
1
1
0
1
0
1
B
IEOR(A,B)
1
0
1
1
0
1
1
0
1
1
1
0
0
0
1
0
Generation of non-uniformly distributed
random numbers
1. By transformation of the uniform distribution.
2. By the von Neumann „hit-and-miss” method.
Uniform distribution transformation
Let x be a random number normally distributed in [0,1]
f ( x)  1, 0  x  1
f ( x)  0, x  0, x  1
A random number with distribution given by g(y) can then be
computed from the inverse of the distribuand G(y) at x provided
that G has the inverse:
dx  g ( y )dy  dG ( y )
y
x  G( y) 
 g (t )dt

y  G 1 ( x)
Transormation of a random number x with a uniform distribution
to random number y with distribund G(y) for continuous (a) and
discrete (b) distributions.
Example: random number with exponential distribution
1
 exp  t  , t  0
g (t )  

0, t  0
x  G (t ) 
1

t
 g (t ' )dt '  1  exp(  t  )
t ' 0
t  G 1 ( x)   ln( 1  x)
An example of exponential distribution generation for various
sampling sizes.
The von Neumann „hit-and-miss” method
f(x)
Accepted points
fmax
Rejected points
fmin
xmin
xmax
x
An efficient algorithm to generate normal
distribution
1. Generate two pseudo-random numbers u1 i u2 from a uniform distribution in
[0,1]. Compute v1=2u1-1 i v2=2u2-1.
2. Compute s=v12+v22.
3. If s>=1, go back to 1.
4. Compute
x1  v1  2 s ln s ,
x2  v2  2 s ln s
These numbers are drawn from a normal distrubition with 0 mean and unit
variance.
To generate a multidimensional normal distribution, the Cholesky
transfomation of the variance-covariance matrix is carried out first and then
variables xi=(LT(x-a))i are generated from normal distributions with zero
mean and unit variance. These are subsequently transformed to the
original variable space by applying the inverse transformation.
The gaussdev.f program from Numerical Recipes.