Download l - Gordon State College

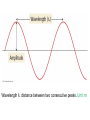
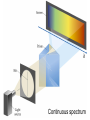
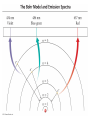
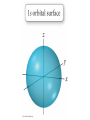
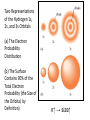
Chapter 7
The Quantum Mechanical
Model of the Atom
Quantum mechanics — microscopic particles
Classical mechanics — macroscopic objects
Some properties of light
Light travels and carries energy
Speed of light c = 3.00 x 108 m/s
Light has many colors
Light can be invisible to human
Light is an electromagnetic radiation
Light is a wave
Wavelength λ: distance between two consecutive peaks. Unit: m
ν = 1/T
c = λ/T
=λν
Wavelength λ: distance between two consecutive peaks. Unit: m
Frequency ν: number of complete wavelengths, or cycles, that
pass a given point each second. Unit: 1/s = s−1 = Hz
Period T: time required for a complete wavelength or cycle to
pass a given point. Unit: s
Demo on Sr salt
λ = 6.50 x 102 nm, what is the frequency of
the red light? What is the period of the light?
ν
Phenomena that could not be explained
by classic mechanics
1. Blackbody radiation
ρ(λ) (kJ/nm)
Energy can only be gained or lost in whole-number
multiples of the quantity hv, a quantum.
Planck’s constant:
h = 6.63 x 10−34 J·s
Phenomena that could not be explained
by classic mechanics
1. Blackbody radiation
2. Photoelectric effect
Photoelectric Effect
Occurs only if
ν > ν0
Electromagnetic radiation can be viewed as a stream
of particles called photons. Energy of one photon is
E = hν
What is the energy of one photon from the red light?
4.61 x 1014 Hz
3.06 x 10−19 J
What is the energy of one photon from a yellow light
whose wavelength is 589 nm?
5.09 x 1014 Hz
3.37 x 10−19 J
ν
Is light a stream of particles or waves?
Electromagnetic Radiation Exhibits Wave
Properties and Particulate Properties
Phenomena that could not be explained
by classic mechanics
1. Blackbody radiation
2. Photoelectric effect
3. Atomic spectra
Pink Floyd: Dark Side of the Moon
λ
Continuous spectrum
Ne gas in tube
Hg
He
H
Neils Bohr
Electrons in an atom can only occupy certain
energy levels
Unknown volatile liquid: methanol CH3OH
Schrödinger’s Equation
Ĥ  E
Ĥ — an operator related to energy
E — energy
Ψ — wave function
Ψ contains all the information of a system
Ψ = Ψ(x,y,z)
x,y,z: coordinates of electrons
H atom
Ψ — wave function
Ψ contains all the information of a system
What is the physical significance of Ψ?
Max Born
│Ψ(x,y,z)│2 — probability density distribution of electrons
Ĥ  E
A specific wave function Ψ is called an orbital.
An atomic orbital is characterized by three
quantum numbers.
Three Quantum Numbers
Principle quantum number n. Only positive integers.
n = 1, 2, 3, 4, · · ·
shell
Angular momentum quantum number l.
l = 0, 1, 2, 3, 4, · · ·, (n − 1)
s
p d
f
g
subshell
Magnetic quantum number ml
ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l
Must remember the possible values for quantum
numbers
One set of n, l, and ml specify One atomic orbital.
EXAMPLE 7.6 Quantum Numbers II
The sets of quantum numbers are each
supposed to specify an orbital. One set,
however, is erroneous. Which one and why?
(a) n = 3; l = 0; ml = 0 (b) n = 2; l = 1; ml = – 1
(c) n = 1; l = 0; ml = 0 (d) n = 4; l = 1; ml = – 2
n = 1, 2, 3, 4, · · ·
l = 0, 1, 2, 3, 4, · · ·, (n − 1)
ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l
Which of the following names are incorrect:
1s, 1p, 7d, 9s, 3f, 4f, 2d
n = 1, 2, 3, 4, · · ·
l = 0, 1, 2, 3, 4, · · ·, (n − 1)
ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l
What are the quantum numbers and names (for
example, 2s, 2p) of the orbitals in the n = 4
principal level? How many n = 4 orbitals exist?
n = 1, 2, 3, 4, · · ·
l = 0, 1, 2, 3, 4, · · ·, (n − 1)
ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l
n = 4; therefore l = 0, 1, 2, and 3
Try “For practice 7.5 and 7.6”
on page 299 and homework questions
How to represent an orbital in 3D?
1) Probability distribution
2) Contour surface
1s orbital of H atom
How to represent an orbital in 3D?
1) Probability distribution
2) Contour surface
90 %
1s orbital of H atom
Two Representations
of the Hydrogen 1s,
2s, and 3s Orbitals
(a) The Electron
Probability
Distribution
(b) The Surface
Contains 90% of the
Total Electron
Probability (the Size of
the Oribital, by
Definition)
n↑ → size↑
Representation of the 2p Orbitals (a) The
Electron Probability Distribution for a 2p Oribtal
(b) The Boundary Surface Representations of all
Three 2p Orbitals
l is related to shape of orbitals
Representation of the 3d Orbitals (a) Electron
Density Plots of Selected 3d Orbitals (b) The
Boundary Surfaces of All of the 3d Orbitals
Chapter 7 Problems
5, 20, 28, 32, 59, 61, 63