* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download l - Gordon State College
Orchestrated objective reduction wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Wave function wikipedia , lookup
Quantum machine learning wikipedia , lookup
Delayed choice quantum eraser wikipedia , lookup
Quantum group wikipedia , lookup
Coherent states wikipedia , lookup
Quantum teleportation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Density matrix wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
History of quantum field theory wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Particle in a box wikipedia , lookup
EPR paradox wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Canonical quantization wikipedia , lookup
Electron scattering wikipedia , lookup
Tight binding wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum key distribution wikipedia , lookup
Molecular orbital wikipedia , lookup
Probability amplitude wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Hidden variable theory wikipedia , lookup
Matter wave wikipedia , lookup
Atomic theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Double-slit experiment wikipedia , lookup
Hydrogen atom wikipedia , lookup
Electron configuration wikipedia , lookup
Atomic orbital wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
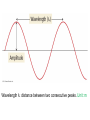
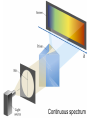
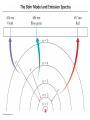
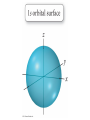
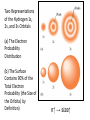
Chapter 7 The Quantum Mechanical Model of the Atom Quantum mechanics — microscopic particles Classical mechanics — macroscopic objects Some properties of light Light travels and carries energy Speed of light c = 3.00 x 108 m/s Light has many colors Light can be invisible to human Light is an electromagnetic radiation Light is a wave Wavelength λ: distance between two consecutive peaks. Unit: m ν = 1/T c = λ/T =λν Wavelength λ: distance between two consecutive peaks. Unit: m Frequency ν: number of complete wavelengths, or cycles, that pass a given point each second. Unit: 1/s = s−1 = Hz Period T: time required for a complete wavelength or cycle to pass a given point. Unit: s Demo on Sr salt λ = 6.50 x 102 nm, what is the frequency of the red light? What is the period of the light? ν Phenomena that could not be explained by classic mechanics 1. Blackbody radiation ρ(λ) (kJ/nm) Energy can only be gained or lost in whole-number multiples of the quantity hv, a quantum. Planck’s constant: h = 6.63 x 10−34 J·s Phenomena that could not be explained by classic mechanics 1. Blackbody radiation 2. Photoelectric effect Photoelectric Effect Occurs only if ν > ν0 Electromagnetic radiation can be viewed as a stream of particles called photons. Energy of one photon is E = hν What is the energy of one photon from the red light? 4.61 x 1014 Hz 3.06 x 10−19 J What is the energy of one photon from a yellow light whose wavelength is 589 nm? 5.09 x 1014 Hz 3.37 x 10−19 J ν Is light a stream of particles or waves? Electromagnetic Radiation Exhibits Wave Properties and Particulate Properties Phenomena that could not be explained by classic mechanics 1. Blackbody radiation 2. Photoelectric effect 3. Atomic spectra Pink Floyd: Dark Side of the Moon λ Continuous spectrum Ne gas in tube Hg He H Neils Bohr Electrons in an atom can only occupy certain energy levels Unknown volatile liquid: methanol CH3OH Schrödinger’s Equation Ĥ E Ĥ — an operator related to energy E — energy Ψ — wave function Ψ contains all the information of a system Ψ = Ψ(x,y,z) x,y,z: coordinates of electrons H atom Ψ — wave function Ψ contains all the information of a system What is the physical significance of Ψ? Max Born │Ψ(x,y,z)│2 — probability density distribution of electrons Ĥ E A specific wave function Ψ is called an orbital. An atomic orbital is characterized by three quantum numbers. Three Quantum Numbers Principle quantum number n. Only positive integers. n = 1, 2, 3, 4, · · · shell Angular momentum quantum number l. l = 0, 1, 2, 3, 4, · · ·, (n − 1) s p d f g subshell Magnetic quantum number ml ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l Must remember the possible values for quantum numbers One set of n, l, and ml specify One atomic orbital. EXAMPLE 7.6 Quantum Numbers II The sets of quantum numbers are each supposed to specify an orbital. One set, however, is erroneous. Which one and why? (a) n = 3; l = 0; ml = 0 (b) n = 2; l = 1; ml = – 1 (c) n = 1; l = 0; ml = 0 (d) n = 4; l = 1; ml = – 2 n = 1, 2, 3, 4, · · · l = 0, 1, 2, 3, 4, · · ·, (n − 1) ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l Which of the following names are incorrect: 1s, 1p, 7d, 9s, 3f, 4f, 2d n = 1, 2, 3, 4, · · · l = 0, 1, 2, 3, 4, · · ·, (n − 1) ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l What are the quantum numbers and names (for example, 2s, 2p) of the orbitals in the n = 4 principal level? How many n = 4 orbitals exist? n = 1, 2, 3, 4, · · · l = 0, 1, 2, 3, 4, · · ·, (n − 1) ml = −l, −l +1, −l + 2, · · · , 0, · · ·, l − 1, l n = 4; therefore l = 0, 1, 2, and 3 Try “For practice 7.5 and 7.6” on page 299 and homework questions How to represent an orbital in 3D? 1) Probability distribution 2) Contour surface 1s orbital of H atom How to represent an orbital in 3D? 1) Probability distribution 2) Contour surface 90 % 1s orbital of H atom Two Representations of the Hydrogen 1s, 2s, and 3s Orbitals (a) The Electron Probability Distribution (b) The Surface Contains 90% of the Total Electron Probability (the Size of the Oribital, by Definition) n↑ → size↑ Representation of the 2p Orbitals (a) The Electron Probability Distribution for a 2p Oribtal (b) The Boundary Surface Representations of all Three 2p Orbitals l is related to shape of orbitals Representation of the 3d Orbitals (a) Electron Density Plots of Selected 3d Orbitals (b) The Boundary Surfaces of All of the 3d Orbitals Chapter 7 Problems 5, 20, 28, 32, 59, 61, 63