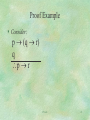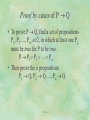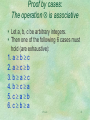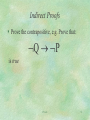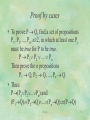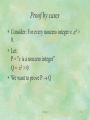Download Proofs

Proofs
Advanced Discrete Mathematics
Jim Skon
Proofs
1
Proofs
 Definition: A theorem is a valid logical
assertion which
can be proved using



other theorems
axioms (statements which are given to be true)
and
rules of inference (logical rules which allow the
deduction of conclusions from premises).
Proofs
2
Proofs
 A lemma (not a “lemon”) is a 'pretheorem' or a result which is needed to
prove a theorem.
 A corollary is a 'post-theorem' or a result
which follows
directly from a theorem.
Proofs
3
Valid reasoning in proofs
 A mathematical proof is a sequence of
statements, such that each statement:
1. is an assumption, or
2. is a proposition already proved, or
3. Follow logically from one or more previous
statements in proof.
Proofs
4
Valid Inference
 Consider: H1 H2 ..... Hn C
where
 Hi are called the hypotheses
and
 C is the conclusion.
Proofs
5
Valid Inference: Argument
 Argument - consists of a collection of
statements, called premises of the argument,
followed by a conclusion statement.
A1
A2
Premises
:
An
A
Conclusion
where  means 'therefore'
or 'it follows 6
Proofs
}
Valid reasoning in proofs
 Example: modus ponens
P  (P  Q)  Q
modus ponens
P: The car is running
Q: The car has gas.
If we know that the car is running (P), we can
prove that (Q) it has gas.

Proofs
7
Rules of Inference
 Rules of Inference - used in proofs, or
arguments, to move from what is known to
what we want to prove.
 modus ponens is a valid rule of inference.
Proofs
8
Valid Argument
 An argument is said to be valid if whenever
all the premises are true, the conclusion is
also true.
 If the premises are true, but the conclusion
false, the argument is said to be invalid.
Proofs
9
Rules of Inference
 Other famous rules of inference:
P
P Q Addition
________________________________
____
P Q
P
Simplification
Proofs
10
Rules of Inference
 Q
P Q
P
Modus Tollens
________________________________
____
P Q
QR
P R
Hypothetical syllogism
Proofs
11
Rules of Inference
 P Q
P
Q
Disjunctive syllogism
________________________________
____
P
Q
P Q
Conjunction
Proofs
12
Rules of Inference
(P Q) (R S)
P R
QS
Constructive dilemma
Proofs
13
Proofs
 Three Techniques

Show true using logical inference
• Assume the hypotheses are true
• Use the rules of inference and logical
equivalences to determine that the conclusion is
true.


Show true by showing that no way exists to
make all premises true but conclusion false
Show false by finding a way to make premises
true but conclusion false.
Proofs
14
Formal Proofs
 To prove an argument is valid or the
conclusion follows
logically from the hypotheses:


Assume the hypotheses are true
Use the rules of inference and logical
equivalences to determine that the
conclusion is true.
Proofs
15
Proof Example
 Consider the following logical argument:
 If horses fly or cows eat artichokes, then
the mosquito is the national bird. If the
mosquito is the national bird then peanut
butter takes good on hot dogs. But
peanut butter tastes terrible on hot dogs.
Therefore, cows don't eat artichokes.
Proofs
16
Proof Example




F Horses fly
A Cows eat artichokes
M The mosquito is the national bird
P Peanut butter tastes good on hot dogs
Proofs
17
Proof Example
 Represent the formal argument using
the variables
1.(FA) M
2.M P
3.P
A
Proofs
18
Proof Example
 Use the hypotheses 1., 2., and 3. and
the above rules of inference and any
logical equivalencies to construct the
proof.
Proofs
19
Proof Example
Assertion
1.(FA) M
2.M P
3.(F A) P`
syll.
4.P
5.(F A)
6.F A
7.A F
8.A
Q. E. D.
Reasons
Hypothesis 1.
Hypothesis 2.
steps 1 and 2 and hypothetical
Hypothesis 3.
steps 3 and 4 and modus tollens
step 5 and DeMorgan
step 6 and commutativity of 'and'
step 7 and simplification
Proofs
20
Proof Example
 Consider:
p  (q  r)
q
p  r
Proofs
21
Proof by contradiction
 Consider:
rs
p s
rq
p  q
Proofs
22
Rules of Inference for
Quantifiers





"xP(x)
P(c) Universal Instantiation (UI)
_______________________________
P(x)
"xP(x) Universal Generalization (UG)
Proofs
23
Rules of Inference for
Quantifiers





P(c)
$xP(x) Existential Generalization (EG)
_______________________________
$xP( x)
P(c) Existential Instantiation (EI)
Proofs
24
Example
Every man has two legs. John Smith is a
man.
Therefore, John Smith has two legs.
Proofs
25
Example
Define the predicates:
M(x): x is a man
L(x): x has two legs
J: John Smith, a member of the universe
The argument becomes
1."x[M(x) L(x)]
2.M( J )
L( J)
Proofs
26
Example
The proof is
1."x[M(x) L(x)] Hypothesis 1
2.M( J ) L(J ) step 1 and UI
3.M(J) Hypothesis 2
4. L( J) steps 2 and 3 and modus
ponens
Q. E. D.
Proofs
27
Fallacies
 Fallacies are incorrect inferences.
 Some common fallacies:



The Fallacy of Affirming the
Consequent
The Fallacy of Denying the
Antecedent
Begging the question or circular
reasoning
Proofs
28
The Fallacy of Affirming the
Consequent
If the butler did it he has blood on his
hands.
The butler had blood on his hands.
Therefore, the butler did it.
 This argument has the form:
P Q
Q
or [(P Q) Q] P
P
 which is not a tautology and therefore not
Proofs
29
a rule of inference!
The Fallacy of Denying the
Antecedent (or the hypothesis)
 If the butler is nervous, he did it.
The butler is really mellow.
Therefore, the butler didn't do it.
 This argument has the form
P Q
P
or [(P Q) P] Q
Q
which is also not a tautology and hence not
a rule of inference.Proofs
30
Begging the question or
circular reasoning
 This occurs when we use the truth of
statement being proved (or something
equivalent) in the proof itself.
 Example:
Conjecture: if x2 is even then x is even.
Proof: If x2 is even then x2 = 2k for
some k. Then x = 2l for some l.
Hence, x must be even.
Proofs
31
Proof Example
 If the law is sufficient, then Christ died in
vain
 The law is sufficient
 Therefore Christ died in vain.
Proofs
32
Example
 Babies are illogical
 Nobody is despised who can manage a
crocodile
 Illogical persons are despised
 Therefore, babies cannot manage crocodiles
Proofs
33
Methods of Proof
 We wish to establish the truth of the
'theorem’
P Q
 P may be a conjunction of other
hypotheses.
 P Q is a conjecture until a proof is
produced.
Proofs
34
Types of proof:
 Vacuous Proof of P  Q


The truth value of P  Q is true if P is false. If
P can be shown false, then P  Q holds.
Thus prove P  Q by showing P is false.
 Example:
If I am both rich and poor then hurricane
Fran was a mild breeze.
 This is of the form: (P P) Q
and the hypotheses form a contradiction.
Proofs
35
Trivial Proof of P  Q
 If we know Q is true then P Q is true!
 Example:
If it's raining today then the empty set is a
subset of every set.
 The assertion is trivially true
independent of the truth of P.
Proofs
36
Direct Proof of P  Q
 Prove Q, using P as an assumption.
 Thus prove P  Q by showing Q is true
whenever P is true.
 assume the hypotheses are true
 use the rules of inference, axioms and
any logical equivalences to establish the
truth of the conclusion.
 Example: the Cows don’t eat artichokes
proof above
Proofs
37
Direct Proof of P  Q
 Theorem: If 6x + 9y = 101, then x or y is not an
integer.
 Proof: (Direct)
Assume 6x + 9y = 101 is true.
Then from the rules of algebra 3(2x + 3y) = 101.
But 101/3 is not an integer so it must be the case that
one
of 2x or 3y is not an integer (maybe both).
Therefore, one of x or y must not be an integer.
Q.E.D.
Proofs
38
Indirect Proof of P  Q
 Prove the contrapositive, e.g. Q  P is
true, using a direct proof methods.
Proofs
39
Indirect Proof of P  Q
 Example:






A perfect number is one which is the sum of
all its divisors except itself. For example, 6
is perfect since 1 + 2 + 3 = 6. So is 28.
Theorem: A perfect number is not a prime.
Proof: (Indirect). We assume the number p
is a prime and show it is not perfect.
But the only divisors of a prime are 1 and
itself.
Hence the sum of the divisors less than p is
1 which is not equal
to
p.
Proofs
40
Hence p cannot be perfect. Q. E. D..
Proof by contradiction
(reductio ad absurdum)
 Assume the negation of the proposition is
true, then derive a contradiction.
 Thus to prove of P  Q, assume P  Q is
true, then derive a contradiction.
Proofs
41
Proof by contradiction








Theorem : 2 is irrational.
Proof: Let P be the proposition “2 is irrational”
Assume P or “2 is rational”
Then 2 = a/b, where a and b are integers and
have no common factors (lowest terms).
Then (2)2 = (a/b)2 is 2 = a2/b2.
Thus 2b2 = a2. Thus a2 is even, implying a is
even. Since a is even, a = 2c for some integer c.
Thus 2b2 = 4c2, so b2 = 2c2. Hence b is even.
Contradiction! A and b are both even, so
Proofs
42
divisible by 2!
Proof by cases of P  Q
 To prove P  Q, find a set of propositions
P1, P2, ..., Pn, n2, in which at least one Pj
must be true for P to be true.
P P1 P2  ...  Pn
 Then prove the n propositions
P1  Q, P2  Q, ..., Pn  Q.
Proofs
43
Proof by cases of P  Q
 Let be the operation 'max' on the set
of integers:
 if a b then ab = max{a, b} = a = ba.
 Theorem: The operation is
associative.
 For all a, b, c
 (ab)c = a (bc).
Proofs
44
Proof by cases:
The operation is associative
 Let a, b, c be arbitrary integers.
 Then one of the following 6 cases must
hold (are exhaustive):
1. a b c
2. a c b
3. b a c
4. b c a
5. c a b
6. c b a
Proofs
45
Proof by cases:
The operation is associative
 Case 1: ab = a, ac = a, and bc = b.
 Hence
(ab)c = a = a(bc).
 Therefore the equality holds for the first
case.
 The proofs of the remaining cases are
similar.
 Q. E. D.
Proofs
46
Vacuous Proof
 Consider the proposition:
If you your grandfather dies as a baby then you
will get an A in this class.
 Proof of this statement:

Your grandfather didn’t die, thus thus the
premise must be false. Thus P  Q must be
true.
Proofs
47
Trivial Proof
 Consider the proposition:

If 3n2 + 5n -2  2n2 + 7n - 16 then n = n2.
P(n).
 Proof of P(0):

0 = 02, thus P(0) is trivially true. QED.
Proofs
48
Direct Proof
 Consider: The sum of two even numbers is even.
 Restate as:

"x:"y: (x is even and y is even)  x + y is even
 Proof:
1. Remember: x is even  $a:x = 2a (definition)
2. Assume x is even and y is even (assume hypothesis)
3. x + y = 2a + 2b
(from 1 and 2)
4. 2a + 2b = 2·(a+b)
5. By 1, 2·(a+b) is even - QED.
Proofs
49
Direct Proof
 Consider: Every multiple of 6 is also a
multiple of 3.
 Rewrite: "x $z$y:(6·x = y  3·z = y)
 Proof:
1. Assume 6x = y (hypothesis)
2. 6x = y can be rewritten as 3 · 2x = y
3. Let z = 2x, then 3·z = y holds. QED.
Proofs
50
Indirect Proofs
 Prove the contrapositive, e.g. Prove that:
Q  P
is true
Proofs
51
Indirect Proofs
 Prove: If x2 is even, then x is even.
 Rewrite: "x : (EVEN(x2)  EVEN(x))
Proofs
52
Indirect Proofs
 Prove: If x2 is even, then x is even
1. "x : (ODD(x)  ODD(x2))
(contrapositive)
2. Assume 1 ODD(n) true for some n
(hypothesis)
3. x is odd  $a:x = 2a + 1
(definition)
4. n = 2a + 1 for some a
(2 & 3)
5. n2 = (2a + 1)2
(substitution)
6. (2a + 1)2
= (2a + 1)(2a + 1)
= 4a 2 + 4a + 1
= 2 (2a2 + 2a) + 1
7. 2 (2a2 + 2a) + 1 is odd
(3 & 6) QED
Proofs
53
Proof by contradiction
 To prove of P  Q, assume P  Q),
derive a contradiction.
 Recall that:
P  Q  P  Q
 Then:
P  Q) P  Q)
 P  Q
(Demorgan’s)
 Thus to prove P  Q we assume P  Q
and show a contradiction.
Proofs
54
Proof by contradiction
 Consider Theorem:
There is no largest prime number.
 This can be stated as
"If x is a prime number, then there exists
another prime y which is greater"
 Formally:
"x $y: (PRIME(x)  PRIME(y)  x < y)
Proofs
55
Proof by contradiction
 There is no largest prime number


Assume largest prime number does exist. Call
this number p.
Restate implication as p is prime, and there
does not exist a prime which is greater.
1. Form a product r = 2 · 3 · 5 · ... p)
(e.g. r is the product of all primes)
2. If we divide r+1 by any prime, it will have
remainder 1
3. r+1 is prime, since any number not divisible by any
prime which is less must be prime.
4. but r+1 > p , which contradicts that p is the greatest
prime number.
QED.
Proofs
56
Proof by cases
 To prove P  Q, find a set of propositions
P1, P2, ..., Pn, n2, in which at least one Pj
must be true for P to be true.
P P1 P2  ...  Pn
Then prove the n propositions
P1  Q, P2  Q, ..., Pn  Q.
 Thus:
P(P1P2...Pn) and
(P1Q)(P2Q)...(PnQ)(PQ)
Proofs
57
Proof by cases
 Consider: For every nonzero integer x ,x2 >
0.
 Let:
P = "x is a nonzero integer”
Q = x2 > 0
 We want to prove P Q
Proofs
58
Proof by cases
 If: P = "x is a nonzero integer”
Q = x2 > 0
 Prove P Q
 P can be broken up into two cases:
P1 = x > 0
P2 = x < 0
 Note that P (P1 P2).
Proofs
59
Proof by cases
 For every nonzero integer x ,x2 > 0.
 Prove each case 

Prove P1 Q:
If x > 0, then x2 > 0, since the product of two
positive numbers is always positive.
Prove P2 Q:
If x < 0, then x2 > 0, since the product of two
negative numbers is always positive.
QED.
Proofs
60
Existence Proofs
 We wish to establish the truth of
$xP( x).
Constructive existence proof:
 Establish P(c) is true for some c in the
universe.
 Then $xP( x) is true by Existential
Generalization (EG).
Proofs
61
Constructive Existence Proofs
 Theorem: There exists an integer
solution to the equation
x 2 + y2 = z2 .
 Proof: Choose x = 3, y = 4, z = 5.
Proofs
62
Constructive Existence Proofs
 Theorem: There exists a bijection from A=
[0,1] to B= [0, 2].
Proof: We build two injections and conclude there must be
a bijection without ever exhibiting the bijection.
Let f be the identity map from A to B.
Then f is an injection (and we conclude that | A | | B | ).
Define the function g from B to A as g(x) = x/4.
Then g is an injection.
Therefore, | B | | A |.
We now apply a previous theorem which states that
if | A | | B | and | B | | A | then | A | = | B |.
Hence, there must be a bijection from A to B.
(Note that we could have chosen g(x) = x/2 and obtained a
bijection directly).
Q. E. D.
Proofs
63
proof
 Assume no c exists which makes P(c) true and
derive a contradiction.
 Example:
Theorem: There exists an irrational number.
Proof:
Assume there doesn’t exist an irrational number.
Then all numbers must be rational.
Then the set of all numbers must be countable.
Then the real numbers in the interval [0, 1] is a
countable set.
But we have already shown this set is not countable.
Hence, we have a contradiction (The set [0,1] is
countable
and not countable).
Therefore, there must exist
Proofs an irrational number.
64
Q. E. D.
" Disproof by Counterexample:
 Recall that $xP(x) "xP(x ).
 To establish that "xP(x ) is true (or
"xP(x) is false) construct a c such that
P(c) is true or P(c) is false.
 In this case c is called a counterexample
to the assertion "xP(x)
Proofs
65
Nonexistence Proofs
 We wish to establish the truth of
$xP( x)
(which is equivalent to "xP(x) ).
 Use a proof by contradiction by
assuming there is a c which makes P(c)
true.
Proofs
66
The (infamous) Halting
Problem
 We wish to establish the nonexistence
of a universal debugging program.
Theorem: There does not exist a
program which will always determine if
an arbitrary program P halts.
We say the Halting Problem is
Yes (Halts)
undecidable.
P1
UDP
P2
No (Infinite Loop)
P3
Proofs
67
Halting Problem
 Proof: Suppose there is such a program
called HALT which will determine if any
input-free program P halts.
HALT(P) prints 'yes' and halts if P halts,
otherwise,
HALT(P) prints 'no' and halts.
We now construct another procedure as follows:
procedure ABSURD;
if HALT(ABSURD) = 'yes' then
while true do print 'ha'
(Note that ABSURD is input-free.)
Proofs
68
Halting Problem
 If ABSURD halts then we execute the loop
which prints unending gales of laughter and
thus the procedure does not halt.
 If ABSURD does not halt then we will exit the
program and halt.
Hence, ABSURD halts if it doesn't
and doesn't halt if it does
 which is an obvious contradiction.
 Hence such a program does not exist.
 Q. E. D.
Proofs
69
Universally Quantified
Assertions
 We wish to establish the truth of
"xP(x)
 We assume that x is an arbitrary
member of the universe and show P(x)
must be true. Using UG it follows that
"xP(x) .
Proofs
70
Universally Quantified
Assertions
 Example:
Theorem: For the universe of integers, x is
even iff x2 is even.
Proof: The quantified assertion is
"x[x is even x2 is even]
Proofs
71
Universally Quantified
Assertions
 Proof:
We assume x is arbitrary.
Recall that P Q is equivalent to (P Q) (QP).
Case 1. We show if x is even then x2 is even using a
direct
proof (the only if part or necessity).
If x is even then x = 2k for some integer k.
Hence, x2 = 4k2 = 2(2k2 ) which is even since it is an
integer which is divisible by 2.
This completes the proof of case 1.
Proofs
72
Universally Quantified
Assertions
Case 2. We show that if x 2 is even then x must be even
(the if part or sufficiency) .
We use an indirect proof:
Assume x is not even and show x2 is not even.
If x is not even then it must be odd.
So, x = 2k + 1 for some k.
Then
x2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1
which is odd and hence not even.
This completes the proof of the second case.
Therefore we have shown x is even iff x2 is even.
Since x was arbitrary, the result follows by UG.
Q.E.D.
Proofs
73
Proofs
74
Proofs
75