Download E-lesson

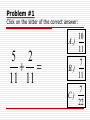
“Working with Fractions”
A Review of
Addition and Subtraction
CLICK HERE TO BEGIN
Goals:
After finishing this activity you will be able to:
Add fractions with like denominators
Add fractions with unlike denominators
Subtract fractions with like denominators
Subtract fractions with unlike denominators
Click to CONTINUE
Fractions
Let’s review the parts of a fraction:
Numerator
1
2
Denominator
Fractions have “Like Denominators” if both fractions have
the exact same number in the denominator.
Example
Fractions have “Unlike Denominators” if they have different
numbers in the denominator.
Example
Click to CONTINUE
“Like Denominators”
2
15
The
same
number
for both
fractions
7
15
RETURN to Lesson
“Unlike Denominators”
7
19
Different
numbers
for each
fraction
5
12
RETURN to Lesson
Adding Fractions with LIKE
Denominators
Let’s say we wanted to solve the problem below:
3
1

5
5
Since these fractions have the same number in
the denominator, all we have to do is add the
numerators!
WATCH it happen!
3 1

5 5
3 1

5
4

5
When adding fractions DO NOT
add the denominators together!
Click to CONTINUE
Adding Fractions with UNLIKE
Denominators
This time, let’s try to solve a problem that is slightly
more challenging:
2
1

3
4
Since the denominators are NOT THE SAME, the first thing
we have to do is make them the same by finding the Least
Common Multiple or the LCM.
Click here to
FIND the LCM.
Step #1: List the multiples of each denominator.
Multiples of 3 : 3, 6, 9, 12, 15, 18, 21 ...
Multiples of 4 : 4, 8, 12, 16, 20, 24, 28 ...
Step #2: Find the SMALLEST number that is in BOTH lists.
Multiples of 3 : 3, 6, 9, 12, 15, 18, 21 ...
Multiples of 4 : 4, 8, 12, 16, 20, 24, 28 ...
This number is the LCM of the denominators!
Click here to find
out what to do
now that we have
the LCM!
We want to make the denominators of both fractions to be equal to the
LCM we just found. We can use multiplication to make that happen!
4 2 8
3 1
3
Since  
and  
4 3 12
3 4 12
2 1

3 4
8
3
Becomes

12 12
Now that we have like
denominators we can add
the fractions like we did last
time!
8 3

12 12
So
83

12
11

12
2 1 11
 
3 4 12
Click to CONTINUE
Subtracting Fractions with LIKE
Denominators
Let’s say we wanted to solve the problem below:
4 3

7 7
Since these fractions have the same number in
the denominator, all we have to do is subtract the
numerators!
WATCH it happen!
4 3

7 7
43

7
1

7
When subtracting fractions DO NOT
subtract the denominators!
Click to CONTINUE
Subtracting Fractions with
UNLIKE Denominators
This time, let’s try to solve a problem that is slightly
more challenging:
5
1

6
4
Since the denominators are NOT THE SAME, the first thing
we have to do is make them the same by finding the Least
Common Multiple or the LCM.
Click here to
FIND the LCM.
Step #1: List the multiples of each denominator.
Multiples of 6 : 6, 12, 18, 24, 30, 36 ...
Multiples of 4 : 4, 8, 12, 16, 20, 24 ...
Step #2: Find the SMALLEST number that is in BOTH lists.
Multiples of 6 : 6, 12, 18, 24, 30, 36 ...
Multiples of 4 : 4, 8, 12, 16, 20, 24 ...
This number is the LCM of the denominators!
Click here to find
out what to do
now that we have
the LCM!
We want to make the denominators of both fractions to be equal to the
LCM we just found. We can use multiplication to make that happen!
2 5 10
3 1
3
Since  
and  
2 6 12
3 4 12
5 1

6 4
10
3
Becomes

12 12
Now that we have like
denominators we can add
the fractions like we did last
time!
10 3

12 12
So
10  3

12
7

12
5 1
7
 
6 4 12
Click to CONTINUE
Let’s Review:
To Add or Subtract fractions with “Like
Denominators:” all you have to do is add or
subtract the numerators.
To Add or Subtract fractions with “Unlike
Denominators:”
 First find the LCM of the denominators.
 Second, multiply each fraction on make the
denominators equal to the LCM
 Finally, add or subtract the numerators
Time to PRACTICE
Problem #1
Click on the letter of the correct answer:
5 2
 
11 11
10
A.)
11
7
B.)
11
7
C.)
22
That is Correct!
5 2 7
 
11 11 11
Go to Problem #2
Sorry that is Incorrect…
Remember, when adding fractions with
the same denominator:
 Add the numerators
 DO NOT add the denominators
 Simplify the fraction when needed
Go to Problem #2
Problem #2
Click on the letter of the correct answer:
4 3
 
7 5
7
A.)
12
7
B.)
35
41
C.)
35
That is Correct!
4 3 41
 
7 5 35
Go to Problem #3
Sorry that is Incorrect…
Remember, when adding fractions with the
different denominators:
 Find the LCM of the denominators
 Use multiplication to change the
denominators
 Add the “new” numerators, but NOT the
“new” denominators
Go to Problem #3
Problem #3
Click on the letter of the correct answer:
8
A.)
0
10 2


21 21
12
B.)
21
8
C.)
21
That is Correct!
10 2
8
 
21 21 21
Go to Problem #4
Sorry that is Incorrect…
Remember, when subtracting fractions with
the same denominator:




Subtract the numerators
DO NOT subtract the denominators
Simplify the fraction when needed
You can NEVER have a zero in the
denominator!
Go to Problem #4
Problem #4
Click on the letter of the correct answer:
3
A.)
55
3 6
 
5 11
3
B.)
6
-3
C.)
55
That is Correct!
3 6
3
 
5 11 55
Click here to FINISH this lesson
Sorry that is Incorrect…
Remember, when subtracting fractions with
the different denominators:
 Find the LCM of the denominators
 Use multiplication to change the
denominators
 Subtract the “new” numerators, but NOT
the “new” denominators
Click here to FINISH this lesson
Congratulations!
You have finished this review lesson.
Please see your teacher to receive
your homework assignment where
you will practice these skills.