Download Math workshop 2 Numbers and Operations

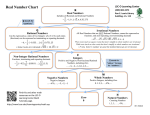
Number Systems
MATH WORKSHOP #2
Directions:
1. Take notes on Rational/Irrational numbers, Exponent rules, square and
square roots, and Scientific notation on your notes sheet using this
powerpoint.
1. Do not copy word for word. Only write down key things you need to
remember!! Show examples to help you study.
2. Remember this is to help you study, so write down what you need to
help you study!
2. Complete the Equations practice and the scientific notation practice.
Complete for homework if not completed in class.
YOU WILL BE ABLE TO:

Distinguish between rational and irrational
numbers
RATIONAL NUMBERS

Rational Numbers
A
rational number is any number that can be
written as a fraction a , where a and b are integers
b
and b  0.
 Rational numbers can also be written as decimals
that either terminate or repeat
 Examples:
5
5,
-14, 12 .75 .333
IRRATIONAL NUMBERS

Irrational numbers can only be written as
decimals that do not terminate or repeat. If a
whole number is not a perfect square, then its
square root is an irrational number.
 Examples

5
2 ≈1.4142135623730950488016…
REAL NUMBERS
Rational numbers
Integers
Whole
numbers
Irrational numbers
Which of the following numbers is rational?
a.
16
b.
13
c.
12
d.
24
Which of the following numbers is rational?
a.
16
b.
13
c.
12
d.
24
Which number is irrational?
a.
b.
c.
 12
1
3
256

d. 4.334
Which number is irrational?
a.
b.
c.
 12
1
3
256

d. 4.334
YOU WILL BE ABLE TO:
Find square roots of perfect squares
 Recognize the (positive) square root of a
number as a length of a side of a square with a
given area
 Recognize square roots as points and as
lengths on a number line
 Understand that the square root of 0 is 0 and
that every positive number has two square
roots that are opposite in sign

Squares and Square Roots
Think about the relationship between the area
of a square and the length of one of its sides.
area = 36 square units
side length = 36 = 6 units
Taking the square root of a number is the inverse of
squaring the number.
62 = 36
36 = 6
Every positive number has two square roots, one positive and
one negative. One square root of 16 is 4, since 4 • 4 = 16. The
other square root of 16 is –4, since (–4) • (–4) is also 16. You
can write the square roots of 16 as ±4, meaning “plus or minus”
4.
Squares and Square Roots
Find the two square roots of each number.
A. 49
–
49 = 7
49 = –7
B. 100
–
100 = 10
10 is a square root, since 10 • 10 = 100.
100 = –10
–10 is also a square root, since
–10 • –10 = 100.
C. 225
–
7 is a square root, since 7 • 7 = 49.
–7 is also a square root, since
–7 • –7 = 49.
225 = 15
15 is a square root, since 15 • 15 = 225.
225 = –15
–15 is also a square root,
since –15 • –15 = 225.
SQUARES AND SQUARE ROOTS
What are the square roots of 100?
a.
b.
c.
d.
-10 only
-10 and 10
10 only
-10,000 and 10,000
SQUARES AND SQUARE ROOTS
What are the square roots of 100?
a.
b.
c.
d.
-10
only
-10 and 10
10 only
-10,000 and 10,000
What is
a. 20
b. 40
c. 800
d. 160,000
400 ?
What is
400 ?
a.20
b.40
c.800
d.160,000
Estimating Square Roots
Each square root is between two integers. Name the
integers. Explain your answer.
72 = 49
Think: What are perfect
squares close to 55?
49 < 55
82 = 64
64 > 55
55
55 is between 7 and 8 because 55 is between
49 and 64.
Each square root is between two integers.
Name the integers. Explain your answer.
80
Think: What are perfect
squares close to 80?
82 = 64
64 < 80
92 = 81
81 > 80
80 is between 8 and 9 because 80 is
between 64 and 81.
Estimating Square Roots
Each square root is between two integers. Name
the integers. Explain your answer.
–
90
Think: What are perfect squares close
to 90?
–92 = 81
81 < 90
–102 = 100
100 > 90
–
90
is between –9 and –10 because 90 is between 81 and 100.
Estimating Square Roots
Each square root is between two integers.
Name the integers.
– 45
Think: What are perfect
squares close to 45?
–62 = 36
36 < 45
–72 = 49
49 > 45
– 45 is between –6 and –7 because 45 is
between 36 and 49.
What point best represents 75 on the number line.
a. W
b. X
c. Y
d. Z
w
x
y
z
What point best represents
75on the number line.
a. W
b. X
c. Y
d. Z
w
x
y
z
YOU WILL BE ABLE TO:

Simplify expressions containing integer
exponents
Properties of Exponents
Products of powers with the same base can be
found by writing each power as a repeated
multiplication.
Notice the relationship between the exponents in
the factors and the exponents in the product
5 + 2 = 7.
Multiplication Properties of Exponents
Example 1: Finding Products of Powers
Simplify.
A.
Since the powers have the same
base, keep the base and add the
exponents.
B.
Group powers with the same base
together.
Add the exponents of powers with
the same base.
Division Properties of Exponents
A quotient of powers with the same base
can be found by writing the powers in a
factored form and dividing out common
factors.
Notice the relationship between the
exponents in the original quotient and the
exponent in the final answer: 5 – 3 = 2.
Division Properties of Exponents
Examples
Simplify.
A.
B.
Examples
Simplify.
Use the Power of a Power Property.
Simplify.
Use the Power of a Power Property.
Zero multiplied by any number is
zero
1
Any number raised to the zero
power is 1.
Scientific Notation
To express any number in scientific notation, write it
as the product of a power of ten and a number
greater than or equal to 1 but less than 10.
Example Translating into standard form.
Write the number in standard notation.
1.35  105
1.35  10
5
10 =5 100,000
1.35  100,000
135,000
Think: Move the decimal right 5 places.
Helpful Hint
A positive exponent means move the decimal to the
right, and a negative exponent means move the
decimal to the left.
Example Translating into standard form.
Write the number in standard notation.
2.7  10–3
2.7  10–3
2.7 
2.7

0.0027
10 –3
=
1
1
1000
1000
1000
Divide by the reciprocal.
Think: Move the decimal left 3 places.
Example Translating into standard form.
Write the number in standard notation.
2.01  104
2.01  104
10 =410,000
2.01  10,000
20,100
Think: Move the decimal right 4 places.