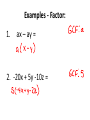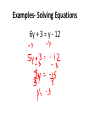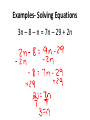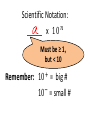* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Algebra 1 Review Chapter 1 Real Numbers, Algebra and
Location arithmetic wikipedia , lookup
Foundations of mathematics wikipedia , lookup
History of mathematics wikipedia , lookup
Bra–ket notation wikipedia , lookup
Abuse of notation wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
System of polynomial equations wikipedia , lookup
Musical notation wikipedia , lookup
Real number wikipedia , lookup
Laws of Form wikipedia , lookup
Big O notation wikipedia , lookup
Large numbers wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Elementary mathematics wikipedia , lookup
Positional notation wikipedia , lookup
History of mathematical notation wikipedia , lookup
Algebra 1 Review
Chapter 1
Real Numbers, Algebra and
Problem Solving
(no exponents)
Algebra 2
Name:____________________
Date:_______________
Types of Numbers (See Flowchart)
What set(s) of numbers do these belong in?
A. -0.52
B. 17
C.
28
D. -2
1
3
Common Properties of Algebra
• Commutative ( + and x)
• Associative (+ and x)
• Distributive
Examples with properties:
• 1. Use the commutative property to rewrite an
equivalent expression to 4x • 7y
• 2. Use the associative property to rewrite an
𝑥
equivalent expression to ( + 8) + 3y
3
• 3. Use the distributive property to simplify:
-3( x – 4y +
5
)
3
Examples - Factor:
1.
ax – ay =
2. -20x + 5y -10z =
Examples - Simplify:
• 1. 2x – (3x – 4) =
• 2. 5x – [ 2x – (3x + 2)] =
• 3. 8x – { 2x – 3[(x-4) – (x-2)]} =
Examples- Solving Equations
6y + 3 = y - 12
Examples- Solving Equations
3n – 8 – n = 7n – 29 + 2n
Scientific Notation:
_____ x
𝑛
10
Must be ≥ 1,
but < 10
Remember:
+
10
= big #
−
10 = small #
Operations with Scientific Notation
Keep the parts separate and adjust when finished:
1)Multiply/Divide numbers in front.
2)Use properties of exponents to evaluate powers
of 10
3)Adjust final scientific notation:
a) If you make the number smaller, you make
the exponent ____________
(by the same number of decimal places)
b) If you make the number bigger, you make
exponent ____________
(by the same number of decimal places)
Examples
3.6 10 4.2 10
5
4
3.42 10
10
8
.
6
10
4
Assignment
Ch 1 Rev/56-58/1-30o, 55-58