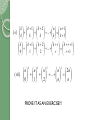Download MATHEMATICS INDUCTION AND BINOM THEOREM

MATHEMATICS INDUCTION
AND
BINOM THEOREM
By : IRA KURNIAWATI, S.Si, M.Pd
Competence Standard
Able to:
 Understand and prove the theorem using
Mathematics Induction
 Apply Binom theorem in the descriptions
of the form of power (a+b)n
MATHEMATICS INDUCTION
One verification method in mathematics.
 Commonly used to prove the theorems
for all integers, especially for natural
numbers.

Mathematics Induction
An important verification tools
 Broadly used to prove statements
connected with discreet objects
(algorithm complexity, graph theorems,
identity and inequality involving integers,
etc.)
 Cannot be used to find/invent
theorems/formula, and can only be used
to prove something

 Mathematics
Induction:
A technique to prove proposition in the
form of n P(n), in which the whole
discussion is about positive integers sets
 Three steps to prove (using mathematics
induction) that “P(n) is true for all n
positive integers”:
1. Basic step: prove that P(1) is true
2. Inductive step: Assumed that P(k) is
true, it can be shown that P(k+1) is
true for all k
3. Conclusion: n P(n) is true
The Steps to prove the theorems using
mathematics induction are :
Supposing p(n) is a statement that will be
proved as true for all natural numbers.
 Step (1) : it is shown that p(1) is true.
 Step (2) : it is assumed that p(k) is true
for k natural number and it is shown that
p(k+1) is true.

When steps 1 and 2 have been done
correctly, it can be concluded that p(n) is
correct for all n natural number
 Step (1) is commonly called as the basic
for induction
 Step (2) is defined as inductive step.

Example:

Using Mathematics Induction, prove that
1
1+2+3+…+n=
n(n+1) for all n natural
2
number
Prove:
Suppose p(n) declares1+2+3+…+n=
1
n(n+1)
2
(i)
(ii)
(iii)
1
2
p(1) is1 = . 1. (2), which means1 = 1,
completely true
It is assumed that p(k) is true for one natural
1
number k, which is 1+2+3+… +k = k(k+1)
2
true
Next, it must be proved that p(k+1) is true,
which is:
1
1+2+3+… +k + (k+1) = 2 (k+1) (k+2)
It should be shown as follows:
1+2+3+… +k + (k+1) = (1+2+3+…+k) +(k+1)
1
= 2 k(k+1)+(k+1)
1
= (k+1) ( k+1)
2
1
=
(k+1) (k+2)
2
1
2
So:1+2+3+… +k + (k+1) = (k+1) (k+2)
which means that p(k+1) is true.
It follows that p(n) is true for all n natural
number
Example 2:
Show that n < 2n for all positive n
natural number.
Solution:
Suppose P(n): proposition “n < 2n”

Basic step:
P(1) is true, because 1 < 21 = 2

Inductive step: Assumed that P(k) is true
for all k natural number, namely k < 2k
We need to prove that P(k+1) is true,
which is: k + 1 < 2k+1
Start from k < 2k
k + 1 < 2k + 1  2k + 2k = 2k+1
So, if k < 2k, then k + 1 < 2k+1 P(k+1) is true
Conclusion:
n < 2n is true for all positive n natural number

The basic of induction is not
always taken from n=1; it can be
taken as suited to the problems
encountered or to statements to
be proved
Supposing p(n) is true for all natural
numbers n ≥ t.
The steps to prove it using mathematics
induction are:
Step (1) : show that p(t) is true
 Step (2) : assume that p(k) is true for
natural number k ≥ t, and show that
p(k+1) is true

Binom Theorem

The combination of r object taken from n
object, exchanged with C(n,r) or  n 
r
 
and formulated as:
n
n!
  
 r  r! (n  r )!
Example:
Suppose there are 5 objects, namely
a,b,c,d, and e. If out of these 5 objects 3
are taken away, the ways to take those 3
objects are:
 n  5!

5.4.3.2.1
  

 10ways
 r  2! 3! (2.1)(3.2.1)
The property of Binom Coefisient
 n n  n
n
i  1  1           ...   
 0  1  2
n
n n n
n
n








so          ...     2
 0  1  2
n
n
n
 n 
n!
n!
 
(ii )   
and 
 k  k!(n  k )!
 n  k  (n  k )! k!
n  n 
 ( symmetrical characteristic )
so    
k  n  k 
(iii) If n and k are natural numbers and n  k, then
 n   n  1  n  1
   
  

 k   k   k  1
(iv) If n, m, and k are natural numbers and n  m  k, so
 n  k   n   n  m
       

 k   m  m  k  m
(v) If n and k are natural numbers and n  k, so
n
 n  1

k    n
k 
 k  1
 k   k  1  k  2 
 n   n  1
  ...     

vi       
k   k   k 
 k   k  1
 k   k  1  k  2 
 k  r   k  r  1
   
  
  ...  
  

0  1   2 
 r   r 1 
2
2
2
2
 n  n  n
 n   2n 
(vii)          ...      
 0  1  2
 n  n 
PROVE IT AS AN EXERCISE!!!