Download Computational thermodynamics - IS MU

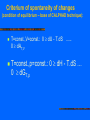
Computational Thermodynamics
Prof. RNDr. Jan Vřešťál, DrSc.
Mgr. Jana Pavlů, Ph.D.
Masaryk University
Brno, Czech Republic







Syllabus
1. Introduction: Computational thermodynamics, past and present of CALPHAD
technique. Thermodynamic basis: laws of thermodynamics, functions of state,
equilibrium conditions, vibrational heat capacity, statistical thermodynamics.
2. Crystallography: connection of thermodynamics with crystallography, crystal
symmetry, crystal structures, sublattice modeling, chemical ordering. Equilibrium
calculations: minimizing of Gibbs energy, equilibrium conditions as a set of
equations, global minimization of Gibbs energy, driving force for a phase.
3. Phase diagrams: definition and types, mapping a phase diagram, implicitly defined
functions and their derivatives. Optimization methods: the principle of the leastsquares method, the weighting factor. Marquardt’s algorithm
4. Sources of thermodynamic data: first principles calculations, the density functional
theory and its approximations, DFT results at 0 K, going to higher temperatures.
Experimental data used for the optimization, calorimetry, galvanic cells, vapor
pressure, equilibria with gases of known activity
5. Sources of phase equilibrium data: thermal analysis, quantitative metallography,
microprobe measurements, two-phase tie-lines, X-ray,electron and neutron diffraction
6. Models for the Gibbs energy: general form of Gibbs-energy model, temperature
and pressure dependences,metastable states,variables for composition dependence
7. Models for the Gibbs energy: modeling particular physical phenomena, models for
the Gibbs energy of solutions, compound energy formalism, the ideal substitutional
solution model, regular solution model
Syllabus - cont.






8 .Models for the excess Gibbs energy: Gibbs energy of mixing, the binary excess
contribution to multicomponent systems, the Redlich-Kister binary excess model,
higher-order excess contributions: Muggianu, Kohler, Colinet and Toop
9. Models for the excess Gibbs energy: associate-solution model, quasi-chemical
model, cluster-variation method, modeling using sublattices: two sublattices model
10. Models for the excess Gibbs energy: models with three or more sublattices,
models for phases with order-disorder transitions Gibbs energy for phases that never
disorder, models for liquids, chemical reactions and models
11. Assessment methodology: literature searching, modeling of the Gibbs energy for
each phase, solubility, thermodynamic data, miscibility gaps, terminal phases model
12. Assessment methodology: modeling intermediate phases, crystal-structure
information, compatibility of models, thermodynamic information, determining
adjustable parameters, decisions to be made during assessment, checking results of
optimization and publishing it.
13. Creating thermodynamic databases: unary data, model compatibility, naming of
phases, validation of databases, nano-materials in structure alloys and lead-free
solders. Examples using databases: Sigma-Phase Formation in Ni-based
anticorrosion Superalloys, Intermetallic Phases in Lead-Free Soldering, Equilibria with
Laves Phases for aircraft engine.
Literature:
N. Saunders, A.P. Miodownik: CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide. Pergamon Press, 1998
H.L. Lukas, S.G. Freis, Bo Sundman: Computational Thermodynamics (The Calphad Method). Cambridge Univ. Press, 2007

Computational thermodynamics (CT) – 1:
Introduction: Computational thermodynamics,
past and present of CALPHAD technique,
thermodynamic basis

Basic thermodynamics: laws of
thermodynamics, functions of state

CALPHAD (CALculation of PHAse Diagrams) technique:
Combining of thermodynamic data, phase equilibrium data and atomistic properties
(e.g.magnetism) into unified consistent model

Historical background:
Josiah Willard Gibbs (1839-1903):
1875, 1878: On the Equilibrium of
Heterogeneous Substances
Johannes Jacobus van Laar (1860-1938):
1908:calculation of phase diagram (melting
line) from Gibbs theory of chemical
potential
Break point: Larry Kaufman (1930-2013)
L.Kaufman, H.Bernstein: Computer Calculations of Phase Diagrams.
N.York, Academic Press 1970
Concept of lattice stability introduced.
L.Kaufman and P.Miodownik
during CALPHAD XXXVIII, Prague 2009
Concept of lattice stability
Lattice stability: G(phase)-G(SER)
SER(Standard Element
Reference): stable state of the
element at p=1 bar and
T=298.15 K
(For some phases hypothetical!)
Example:
determination of real and
hypothetical melting points
of Fe
N.Saunders, P.Miodownik: CALPHAD, Pergamon 1998, p.155
Today applications:
From Gibbs energies to simulations of transformations of real
multicomponent materials – examples:
Example: Cr-Ni: Phase diagram and Scheil solidifications
Thermocalc (TC) - demo
JMatPro - demo
Annual conferences: 2009 Prague, Czech Republic, May 17-22, 2009
2014 Changsha, China, June 1-6, 2014
Solidification: Scheil-Guliver model (TC)
(no diffusion in solid, instant diffusion in liquid)
Alloy Cr-Ni10
Phase diagram
LIQ
BCC
FCC
Solidification diagram (Scheil)
Solidification: Scheil-Guliver model (JMatPro)
Demo-version: Load data – example:
Today applications:
From Gibbs energies to simulations of transformations of real
multicomponent materials
Chemical potential and „thermodynanamic factor“ (second derivative of
Gibbs energy) – Simulation of diffusion proceses (DICTRA)
„Thermodynamic factor“:
(1+ (dln/dlnx))
: activity coefficient
x: molar fraction
Example:
Simulation of phase transformation:
dissolution of cementite in Cr-austenite
Lucas H.L., Fries S.G., Sundman B.: Computational
Thermodynamics, Cambridge Univ.Press., 2007.- (LFS-CT)
Volume fraction of carbide during dissolution
of cementite in Cr-austenite
CT for phase transformation simulations
For experimental researchers:
test compatibility of experimental results and literature
data
For theoreticians:
improve usefulness of results by combining with
experimental data
Condition for application of CALPHAD
technique:
Thermodynamic database – consistency of database:
Unary data: SGTE (mostly above room temperature)
A.T.Dinsdale: Calphad, 15 (1991) 317-425
78 elements
Gibbs energies for SER - phases, FCC -, BCC -, HCP – phases, other phases
Continuous updating of data: SGTE ver.4.1
Condition for application of CALPHAD technique:
Construction of databases: expertise and experience
Examples:
solders (solder.tdb)
Ag, Au, Bi, Cu, In,
steels (steel-ex.tdb)
Al, C, Co, Cr, Cu, Fe, Mn,
Ni, Pb, Pd, Sb,Sn,Zn
Mo, N, Nb, Ni, Si, Ta, V, W
Rules for creation of consistent database:
- Consistent with respect to the temperature, pressure and conceration
dependence for the Gibbs energy for the different phases
- Consistent with respect to models and names used for the description of
equivalent phases existing in different systems
- Consistent with respect to description of the Gibbs energy for an element or
compound of given crystallographic structure
Many commercial databases available
Ab initio (DFT) calculations in assessment
technique
Examples: Gibbs energy of metastable structures,Y.Wang et al.: Calphad 28 (2004) 78-90
CT - describes equilibrium states
Thermodynamic functions X(p,T,x) used (X = H, G, S, Cp)
X(p,T,x) can be extrapolated – simulation models
Cp = a + bT + cT-1 + dT-2 (not to 0 K !)
X(p,T,x) contains adjustable parameters (polynomials)
GE = x1 (1-x1) [Lo + L1(x1 – x2) + L2(x1-x2)2 + …]
CT – for multicomponent systems of
technological interest now
Example:
Superaustenites –Laves vs. Sigma phases
M.Svoboda et al.: Z.Metallkde 95 (2004) 1025
(M.Kraus et al. Accepted in IJMR)
Avesta 254, 700 C
Nicrofer 3127, 700 C
14
Volume fraction, %
12
10
8
6
4
Laves
2
Sigma
0
0
1000
2000
3000
4000
5000
6000
7000
Time, hours
Amount of sigma phase successfully predicted by CALPHAD method
CT for phase equilibrium determination
CT for determination of phase composition –
(microstructure determines properties of sample)
Example: In – Sb – Sn system. Predicted section checked by experiment
D. Manasijevic et al.: Journal of Alloys and Compounds 450 (2008) 193
CALPHAD: calculating of phase diagrams from thermodynamic
models with parameters adjusted to the available experimental
data
CALPHAD technique: selecting model for phases that can be
extrapolated in x- and T- ranges
CALPHAD method: using of available experimental and
theoretical data to assess the parameters of the Gibbs energy
models for phases
Computational thermodynamics (CT): describes
the use of these models and parameters stored in
thermodynamic databases for various applications
CALPHAD for dilute solutions
Simple one Henrian coefficient (B in solvent A) –
non CALPHAD procedure – not for multicomponent
systems
Calphad technique: two parameters:
Solvent phase consisting of pure B (lattice stability) +
interaction parameter between A and B
In multicomponent thermodynamics – Calphad
technique is advantageous.
Development of models and techniques
Sublattice (polynomial) models: inspired by crystallography
2 – 4 sublattices
Minimization methods:
- solution of the system of nonlinear equations
- constrained minimization (total Gibbs energy of the system)
Codes: Thermocalc, MTDATA, Pandat, FACTSage,,…
Development of databases
Unary data - SGTE
Binary data – models for Gibbs energy
- expressions for excess Gibbs energy (GE)
Examples: GE - Polynomials: Redlich-Kister (1948)
advantages - disadvantages
Other polynomials (TAP…)
Other polynomials for GE
Calphad 6 (1982) 297
Basic Thermodynamics

Temperature – thermal equilibrium
Zeroth law of thermodynamics:
A = B, A = C  B = C
Thermometers, temperature scales
Atkins P.W.: Physical Chemistry
Thermodynamics - study of energy
transformations
System and its surroundings

System - isolated
- closed
- open
Intensive and extensive variables (X, X/N, Xm, X/Ni)
Atkins P.W.:Physical Chemistry
Work and heat






Total energy of the system = internal energy U
Absolute value is not known, only changes
 U = Ufin. - Uinitial
(sign convention – with respect to the system)
U = state function
(depends only on the initial and final states)
Work and
heat
Atkins P.W.: Physical Chemistry
State function
Atkins P.W.: Physical Chemistry
First law of thermodynamics


Axiom: Internal energy of the CLOSED system
is constant, unless is changed by performing
work on it or by heating of it
U=q+w
Isothermal process – no change of  U
Atkins P.W.: Physical Chemistry
Enthalpy
Change of the internal energy of the system:
dU = dq + dwexpans.+ dwrest.
dU = dq
[V=const., dwost.= 0]
If it is V const. a p=const. (wexpans 0): dU dq.








Definition of new function: H = U + pV - state function!
dH = dU + d(p.V) = dU + p.dV + V.dp
dU = dq - pexpans. dV + dwrest.
dH = dq - pexpans.dV + dwrest. + p.dV + V.dp
in equilibrum: pexpans.=p, dwrest.=0 (dp=0)
dH = dq
[p = const., dwrest.=0]
H =  dq (od qinitial. do qfin.) :
[p = const., dwrest.=0]
Calorimetry
•Cp= ( H / T)p
•Ho(T2) = Ho(T1) +Cp dT, (from i to f states)
(Kirchhoff law)
Second Law of thermodynamics: spontanesus
changes – direction of changes
Atkins P.W.: Physical Chemistry
Second law of thermodynamics
Axiom : Entropy of ISOLATED system
is raising in the course of spontaneous changes
Stot.  0.
Statistical definition: S=kB.ln W, (Boltzmann)
(W = weight of state)
Entropy changes:




 Ssurr=qrev/Tsurr
dS - dq/T  0
(reversible changes, role of surounding)
Clausius inequality
During phase transformations:
 Stransf.=qtransf./Ttransf (phase transformations)
Entropy during heating


p=const.:
 S = (Cp/T) dT, (from Ti to Tf),
(qrev= H)
V=const.
 S = (CV/T) dT, (from Ti to Tf),
(qrev= U)
Atkins P.W.: Physical Chemistry
Third law of thermodynamics – entropy value
at T= 0 K





Axiom (III.law):
If the entropy of every element in the most
stable state at 0K is taken as zero,
then every substance has a positive entropy
which at T=0 may become zero,
and which does become zero for all perfect
crystalline substances, including compounds
(Value S=0 is a convention)
Helmholtz and Gibbs energies


Clausius inequality: dS - dq/T  0
(thermal equilibrium - temperature T)
2 examples of heat transfer:
V=const. a p=const.
1. V=const., dqV= dU






dS - dU/T  0
TdS  dU resp. 0 dU-TdS
(assumptions:T,V=const.,dwnonexpans =0)
a. dU=0 ...... dSU,V  0
b. dS=0 ...... 0  dUS,V
a,b - criteria of spontaneity of the process
2. p=const., dqp = dH






dS - dH/T  0
TdS  dH resp. 0 dH - TdS
(assumptions:T,p=const.,dwnonexpans =0)
a. dH=0 ... dSH,p 0
b. dS=0 ... 0 dHS,p
a,b - criteria of spontaneity of process
At T=const:




0  dU-T.dS (V=const.), resp.
0  dH-T.dS (p=const.)
Introduce:
Helmholtz energy (function):
Gibbs energy (function):
A(F)= U - T.S
G = H - T.S
Criterium of spontaneity of changes
(condition of equilibrium – base of CALPHAD technique):


T=const.,V=const.: 0  dU - T.dS ......
0  dAT,V
T=const.,p=const.: 0  dH - T.dS …
0  dGT,p
Comparing with total differential:

dG = ( G/ T)p dT + ( G/ p)T dp
( G/ T)p = -S,
( G/ p)T = V
Gibbs-Helmholtz equation







S= (H-G)/T =
-( G/ T)p = S
Rewrite:
( G/ T)p - G/T = - H/T
Left side we can write as:
T( (G/T)/ T)p = -H/T,
Rewrite :
( (G/T)/ T)p = -H/T2
Chemical potencial of open system
(more components)

dG=( G/ p)T,ndp+( G/ T)p,ndT+
( G/ n1)p,T,n2dn1+( G/ n2)p,T,n1dn2
We know that: ( G/ p)T,n=V, ( G/ T)p,n = -S

We introduce:
1 = ( G/ n1)p,T,n2

2= ( G/ n2)p,T,n1
chemical potential (expressed by G):
G = V dp – S dT + j j dnj
Questions for learning
1.What is CALPHAD method and what practical problems can be
solved using this method?
2. Give advantages and disadvantages of softwares which can be used
for this tasks.
3. Explain basic laws of thermodynamics and define thermodynamic
functions on their basis.
4. What is state function and what property of it can be used in
thermodynamics?
5. Describe condition of equilibrium by using of Gibbs energy
(Helmholtz energy) and by using of chemical potential.