* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Computational thermodynamics - IS MU
Physical organic chemistry wikipedia , lookup
Thermodynamic equilibrium wikipedia , lookup
Statistical mechanics wikipedia , lookup
Chemical potential wikipedia , lookup
Vapor–liquid equilibrium wikipedia , lookup
Marcus theory wikipedia , lookup
Heat transfer physics wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Gibbs paradox wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Transition state theory wikipedia , lookup
Determination of equilibrium constants wikipedia , lookup
Equilibrium chemistry wikipedia , lookup
Maximum entropy thermodynamics wikipedia , lookup
Chemical equilibrium wikipedia , lookup
Non-equilibrium thermodynamics wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
History of thermodynamics wikipedia , lookup
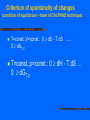
Computational Thermodynamics Prof. RNDr. Jan Vřešťál, DrSc. Mgr. Jana Pavlů, Ph.D. Masaryk University Brno, Czech Republic Syllabus 1. Introduction: Computational thermodynamics, past and present of CALPHAD technique. Thermodynamic basis: laws of thermodynamics, functions of state, equilibrium conditions, vibrational heat capacity, statistical thermodynamics. 2. Crystallography: connection of thermodynamics with crystallography, crystal symmetry, crystal structures, sublattice modeling, chemical ordering. Equilibrium calculations: minimizing of Gibbs energy, equilibrium conditions as a set of equations, global minimization of Gibbs energy, driving force for a phase. 3. Phase diagrams: definition and types, mapping a phase diagram, implicitly defined functions and their derivatives. Optimization methods: the principle of the leastsquares method, the weighting factor. Marquardt’s algorithm 4. Sources of thermodynamic data: first principles calculations, the density functional theory and its approximations, DFT results at 0 K, going to higher temperatures. Experimental data used for the optimization, calorimetry, galvanic cells, vapor pressure, equilibria with gases of known activity 5. Sources of phase equilibrium data: thermal analysis, quantitative metallography, microprobe measurements, two-phase tie-lines, X-ray,electron and neutron diffraction 6. Models for the Gibbs energy: general form of Gibbs-energy model, temperature and pressure dependences,metastable states,variables for composition dependence 7. Models for the Gibbs energy: modeling particular physical phenomena, models for the Gibbs energy of solutions, compound energy formalism, the ideal substitutional solution model, regular solution model Syllabus - cont. 8 .Models for the excess Gibbs energy: Gibbs energy of mixing, the binary excess contribution to multicomponent systems, the Redlich-Kister binary excess model, higher-order excess contributions: Muggianu, Kohler, Colinet and Toop 9. Models for the excess Gibbs energy: associate-solution model, quasi-chemical model, cluster-variation method, modeling using sublattices: two sublattices model 10. Models for the excess Gibbs energy: models with three or more sublattices, models for phases with order-disorder transitions Gibbs energy for phases that never disorder, models for liquids, chemical reactions and models 11. Assessment methodology: literature searching, modeling of the Gibbs energy for each phase, solubility, thermodynamic data, miscibility gaps, terminal phases model 12. Assessment methodology: modeling intermediate phases, crystal-structure information, compatibility of models, thermodynamic information, determining adjustable parameters, decisions to be made during assessment, checking results of optimization and publishing it. 13. Creating thermodynamic databases: unary data, model compatibility, naming of phases, validation of databases, nano-materials in structure alloys and lead-free solders. Examples using databases: Sigma-Phase Formation in Ni-based anticorrosion Superalloys, Intermetallic Phases in Lead-Free Soldering, Equilibria with Laves Phases for aircraft engine. Literature: N. Saunders, A.P. Miodownik: CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide. Pergamon Press, 1998 H.L. Lukas, S.G. Freis, Bo Sundman: Computational Thermodynamics (The Calphad Method). Cambridge Univ. Press, 2007 Computational thermodynamics (CT) – 1: Introduction: Computational thermodynamics, past and present of CALPHAD technique, thermodynamic basis Basic thermodynamics: laws of thermodynamics, functions of state CALPHAD (CALculation of PHAse Diagrams) technique: Combining of thermodynamic data, phase equilibrium data and atomistic properties (e.g.magnetism) into unified consistent model Historical background: Josiah Willard Gibbs (1839-1903): 1875, 1878: On the Equilibrium of Heterogeneous Substances Johannes Jacobus van Laar (1860-1938): 1908:calculation of phase diagram (melting line) from Gibbs theory of chemical potential Break point: Larry Kaufman (1930-2013) L.Kaufman, H.Bernstein: Computer Calculations of Phase Diagrams. N.York, Academic Press 1970 Concept of lattice stability introduced. L.Kaufman and P.Miodownik during CALPHAD XXXVIII, Prague 2009 Concept of lattice stability Lattice stability: G(phase)-G(SER) SER(Standard Element Reference): stable state of the element at p=1 bar and T=298.15 K (For some phases hypothetical!) Example: determination of real and hypothetical melting points of Fe N.Saunders, P.Miodownik: CALPHAD, Pergamon 1998, p.155 Today applications: From Gibbs energies to simulations of transformations of real multicomponent materials – examples: Example: Cr-Ni: Phase diagram and Scheil solidifications Thermocalc (TC) - demo JMatPro - demo Annual conferences: 2009 Prague, Czech Republic, May 17-22, 2009 2014 Changsha, China, June 1-6, 2014 Solidification: Scheil-Guliver model (TC) (no diffusion in solid, instant diffusion in liquid) Alloy Cr-Ni10 Phase diagram LIQ BCC FCC Solidification diagram (Scheil) Solidification: Scheil-Guliver model (JMatPro) Demo-version: Load data – example: Today applications: From Gibbs energies to simulations of transformations of real multicomponent materials Chemical potential and „thermodynanamic factor“ (second derivative of Gibbs energy) – Simulation of diffusion proceses (DICTRA) „Thermodynamic factor“: (1+ (dln/dlnx)) : activity coefficient x: molar fraction Example: Simulation of phase transformation: dissolution of cementite in Cr-austenite Lucas H.L., Fries S.G., Sundman B.: Computational Thermodynamics, Cambridge Univ.Press., 2007.- (LFS-CT) Volume fraction of carbide during dissolution of cementite in Cr-austenite CT for phase transformation simulations For experimental researchers: test compatibility of experimental results and literature data For theoreticians: improve usefulness of results by combining with experimental data Condition for application of CALPHAD technique: Thermodynamic database – consistency of database: Unary data: SGTE (mostly above room temperature) A.T.Dinsdale: Calphad, 15 (1991) 317-425 78 elements Gibbs energies for SER - phases, FCC -, BCC -, HCP – phases, other phases Continuous updating of data: SGTE ver.4.1 Condition for application of CALPHAD technique: Construction of databases: expertise and experience Examples: solders (solder.tdb) Ag, Au, Bi, Cu, In, steels (steel-ex.tdb) Al, C, Co, Cr, Cu, Fe, Mn, Ni, Pb, Pd, Sb,Sn,Zn Mo, N, Nb, Ni, Si, Ta, V, W Rules for creation of consistent database: - Consistent with respect to the temperature, pressure and conceration dependence for the Gibbs energy for the different phases - Consistent with respect to models and names used for the description of equivalent phases existing in different systems - Consistent with respect to description of the Gibbs energy for an element or compound of given crystallographic structure Many commercial databases available Ab initio (DFT) calculations in assessment technique Examples: Gibbs energy of metastable structures,Y.Wang et al.: Calphad 28 (2004) 78-90 CT - describes equilibrium states Thermodynamic functions X(p,T,x) used (X = H, G, S, Cp) X(p,T,x) can be extrapolated – simulation models Cp = a + bT + cT-1 + dT-2 (not to 0 K !) X(p,T,x) contains adjustable parameters (polynomials) GE = x1 (1-x1) [Lo + L1(x1 – x2) + L2(x1-x2)2 + …] CT – for multicomponent systems of technological interest now Example: Superaustenites –Laves vs. Sigma phases M.Svoboda et al.: Z.Metallkde 95 (2004) 1025 (M.Kraus et al. Accepted in IJMR) Avesta 254, 700 C Nicrofer 3127, 700 C 14 Volume fraction, % 12 10 8 6 4 Laves 2 Sigma 0 0 1000 2000 3000 4000 5000 6000 7000 Time, hours Amount of sigma phase successfully predicted by CALPHAD method CT for phase equilibrium determination CT for determination of phase composition – (microstructure determines properties of sample) Example: In – Sb – Sn system. Predicted section checked by experiment D. Manasijevic et al.: Journal of Alloys and Compounds 450 (2008) 193 CALPHAD: calculating of phase diagrams from thermodynamic models with parameters adjusted to the available experimental data CALPHAD technique: selecting model for phases that can be extrapolated in x- and T- ranges CALPHAD method: using of available experimental and theoretical data to assess the parameters of the Gibbs energy models for phases Computational thermodynamics (CT): describes the use of these models and parameters stored in thermodynamic databases for various applications CALPHAD for dilute solutions Simple one Henrian coefficient (B in solvent A) – non CALPHAD procedure – not for multicomponent systems Calphad technique: two parameters: Solvent phase consisting of pure B (lattice stability) + interaction parameter between A and B In multicomponent thermodynamics – Calphad technique is advantageous. Development of models and techniques Sublattice (polynomial) models: inspired by crystallography 2 – 4 sublattices Minimization methods: - solution of the system of nonlinear equations - constrained minimization (total Gibbs energy of the system) Codes: Thermocalc, MTDATA, Pandat, FACTSage,,… Development of databases Unary data - SGTE Binary data – models for Gibbs energy - expressions for excess Gibbs energy (GE) Examples: GE - Polynomials: Redlich-Kister (1948) advantages - disadvantages Other polynomials (TAP…) Other polynomials for GE Calphad 6 (1982) 297 Basic Thermodynamics Temperature – thermal equilibrium Zeroth law of thermodynamics: A = B, A = C B = C Thermometers, temperature scales Atkins P.W.: Physical Chemistry Thermodynamics - study of energy transformations System and its surroundings System - isolated - closed - open Intensive and extensive variables (X, X/N, Xm, X/Ni) Atkins P.W.:Physical Chemistry Work and heat Total energy of the system = internal energy U Absolute value is not known, only changes U = Ufin. - Uinitial (sign convention – with respect to the system) U = state function (depends only on the initial and final states) Work and heat Atkins P.W.: Physical Chemistry State function Atkins P.W.: Physical Chemistry First law of thermodynamics Axiom: Internal energy of the CLOSED system is constant, unless is changed by performing work on it or by heating of it U=q+w Isothermal process – no change of U Atkins P.W.: Physical Chemistry Enthalpy Change of the internal energy of the system: dU = dq + dwexpans.+ dwrest. dU = dq [V=const., dwost.= 0] If it is V const. a p=const. (wexpans 0): dU dq. Definition of new function: H = U + pV - state function! dH = dU + d(p.V) = dU + p.dV + V.dp dU = dq - pexpans. dV + dwrest. dH = dq - pexpans.dV + dwrest. + p.dV + V.dp in equilibrum: pexpans.=p, dwrest.=0 (dp=0) dH = dq [p = const., dwrest.=0] H = dq (od qinitial. do qfin.) : [p = const., dwrest.=0] Calorimetry •Cp= ( H / T)p •Ho(T2) = Ho(T1) +Cp dT, (from i to f states) (Kirchhoff law) Second Law of thermodynamics: spontanesus changes – direction of changes Atkins P.W.: Physical Chemistry Second law of thermodynamics Axiom : Entropy of ISOLATED system is raising in the course of spontaneous changes Stot. 0. Statistical definition: S=kB.ln W, (Boltzmann) (W = weight of state) Entropy changes: Ssurr=qrev/Tsurr dS - dq/T 0 (reversible changes, role of surounding) Clausius inequality During phase transformations: Stransf.=qtransf./Ttransf (phase transformations) Entropy during heating p=const.: S = (Cp/T) dT, (from Ti to Tf), (qrev= H) V=const. S = (CV/T) dT, (from Ti to Tf), (qrev= U) Atkins P.W.: Physical Chemistry Third law of thermodynamics – entropy value at T= 0 K Axiom (III.law): If the entropy of every element in the most stable state at 0K is taken as zero, then every substance has a positive entropy which at T=0 may become zero, and which does become zero for all perfect crystalline substances, including compounds (Value S=0 is a convention) Helmholtz and Gibbs energies Clausius inequality: dS - dq/T 0 (thermal equilibrium - temperature T) 2 examples of heat transfer: V=const. a p=const. 1. V=const., dqV= dU dS - dU/T 0 TdS dU resp. 0 dU-TdS (assumptions:T,V=const.,dwnonexpans =0) a. dU=0 ...... dSU,V 0 b. dS=0 ...... 0 dUS,V a,b - criteria of spontaneity of the process 2. p=const., dqp = dH dS - dH/T 0 TdS dH resp. 0 dH - TdS (assumptions:T,p=const.,dwnonexpans =0) a. dH=0 ... dSH,p 0 b. dS=0 ... 0 dHS,p a,b - criteria of spontaneity of process At T=const: 0 dU-T.dS (V=const.), resp. 0 dH-T.dS (p=const.) Introduce: Helmholtz energy (function): Gibbs energy (function): A(F)= U - T.S G = H - T.S Criterium of spontaneity of changes (condition of equilibrium – base of CALPHAD technique): T=const.,V=const.: 0 dU - T.dS ...... 0 dAT,V T=const.,p=const.: 0 dH - T.dS … 0 dGT,p Comparing with total differential: dG = ( G/ T)p dT + ( G/ p)T dp ( G/ T)p = -S, ( G/ p)T = V Gibbs-Helmholtz equation S= (H-G)/T = -( G/ T)p = S Rewrite: ( G/ T)p - G/T = - H/T Left side we can write as: T( (G/T)/ T)p = -H/T, Rewrite : ( (G/T)/ T)p = -H/T2 Chemical potencial of open system (more components) dG=( G/ p)T,ndp+( G/ T)p,ndT+ ( G/ n1)p,T,n2dn1+( G/ n2)p,T,n1dn2 We know that: ( G/ p)T,n=V, ( G/ T)p,n = -S We introduce: 1 = ( G/ n1)p,T,n2 2= ( G/ n2)p,T,n1 chemical potential (expressed by G): G = V dp – S dT + j j dnj Questions for learning 1.What is CALPHAD method and what practical problems can be solved using this method? 2. Give advantages and disadvantages of softwares which can be used for this tasks. 3. Explain basic laws of thermodynamics and define thermodynamic functions on their basis. 4. What is state function and what property of it can be used in thermodynamics? 5. Describe condition of equilibrium by using of Gibbs energy (Helmholtz energy) and by using of chemical potential.