Download Modern Geometries: Non-Euclidean, Projective, and Discrete

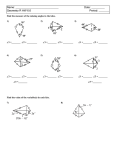
Ch. 1: Some History
References
•Modern Geometries: Non-Euclidean, Projective, and Discrete 2nd ed by Michael Henle
•Euclidean and Non-Euclidean Geometries: Development and History 4th ed by Marvin
Jay Greenberg
•A Short History of Geometry, http://geometryalgorithms.com/history.htm
•Gilbert Lecture Notes,
http://www.math.sc.edu/~sharpley/math532/Book_Gilbert.pdf
•Modern Geometries: The History of Geometry, Part 3 by Monica Garcia Pinillos
http://cerezo.pntic.mec.es/mgarc144/marcohistoria/Modern%20Geometries.pdf
What is Geometry?
• “geometry” comes from the Greek
geometrein
• geo – “earth”
• metrein – “to measure”
• Several thousand years old – used in
agriculture and building.
• Size, shape and position of two
dimensional plane figures and three
dimensional objects.
Some Characteristics of
Euclidean Geometry
•
•
•
•
Deductive science
Visualization
Intuition
Practical
Ancient Egyptians
• Herodotus (Greek, 5th cent. B.C.) : Egyptian
surveyors originated geometry
• Construction of the pyramids
• Egyptian geometry: collection of rules for
calculation (some correct, some incorrect)
without justification
Babylonians
• More interested in arithmetic (used base
60)
• Had calculations for areas and volumes
• Pythagorean theorem
• Corresponding sides of similar triangles
are proportional
• 360o in a circle
Ancient India
• Shapes and sizes of altars and temples
• Sulbasutra (2000 B.C.) contains
Pythagorean theorem
• The number zero!
Ancient Chinese
• Jiuzhang suanshu (Nine Chapters on the
Mathematical Arts)
• Surveying, agriculture, engineering,
taxation
• Pythagorean theorem with a diagram to
help explain why it is correct
Knowledge of these ancient
civilizations
• Calculate the area of simple rectilinear
shapes
• The ratio of circumference to diameter in
circles is constant & rough approximations
to that constant
• The area of a circle is half the
circumference times half the diameter
• Developed to solve practical problems
• Evolved out of experiments
Ancient Greeks
• Thales of Miletus (6th cent. B.C.)
• Development of theorems with proofs
about abstract entities
• Dialectics: the art of arguing well
Greek Mathematicians
•
•
•
•
•
•
•
•
Pythagoras of Samos (569-475 BC)
Hippocrates of Chios (470-410 BC)
Plato (427-347 BC)
Theaetetus of Athens (417-369 BC)
Eudoxus of Cnidus (408-355 BC)
Euclid of Alexandria (325-265 BC)
Archimedes of Syracuse (287-212 BC)
Hypatia of Alexandria (370-415 AD)
Euclid of Alexandria (325-265 BC)
•
•
•
•
•
•
The Elements
I-IV, VI : plane geometry
XI-XIII : solid geometry
V: Eudoxus’ theory of proportions
VII-IX : the theory of whole numbers
X : Theatetus’ classification of certain
types of irrationals
Euclid’s Postulates (Henle, pp. 7-8)
1. A straight line may be drawn from a point to
any other point.
2. A finite straight line may be produced to any
length.
3. A circle may be described with any center and
any radius.
4. All right angles are equal.
5. If a straight line meet two other straight lines
so that as to make the interior angles on one
side less than two right angles, the other
straight lines meet on that side of the first line.
Euclid’s Parallel Postulate
• “Given a line and a point not on that line,
there exists one and only one line through
the given point parallel to the given line.”
• Contains two ideas: existence and
uniqueness.
• No proof of a contradiction from the denial
of either the existence or the uniqueness
part of the of the parallel postulate is
possible.
Two alternatives to the parallel
postulate
• Elliptic Geometry: There is no line parallel
to some line through some point.
(Chapter 11 in Henle)
• Hyperbolic Geometry: There exist at least
two lines parallel to some line through
some point.
(Chapters 7-10 in Henle)
Further Developments
•
•
•
•
•
•
•
•
•
•
•
•
Rene Descartes (1596-1650)
Pierre de Fermat (1601-1665)
Girard Desargues (1591-1661)
Blaise Pascal (1623-1662)
Leonhard Euler (1707-1783)
Carl Friedrich Gauss (1777-1855)
Hermann Grassmann (1809-1877)
Arthur Cayley (1821-1895)
Bernhard Riemann (1826-1866)
Felix Klein (1849-1925)
David Hilbert (1862-1943)
Donald Coxeter (1907-2003)