Download Slide 1

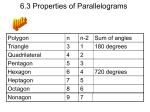
Quadrilaterals

§ 8.1 Quadrilaterals

§ 8.2 Parallelograms

§ 8.3 Tests for Parallelograms

§ 8.4 Rectangles, Rhombi, and Squares

§ 8.5 Trapezoids
Quadrilaterals
You will learn to identify parts of quadrilaterals and find the
sum of the measures of the interior angles of a quadrilateral.
1) Quadrilateral
2) Consecutive
3) Nonconsecutive
4) Diagonal
Quadrilaterals
four sides and ____
four vertices.
A quadrilateral is a closed geometric figure with ____
Quadrilaterals
Not Quadrilaterals
The segments of a quadrilateral intersect only at their endpoints.
Special types of quadrilaterals include squares and rectangles.
Quadrilaterals
Quadrilaterals are named by listing their vertices in order.
There are several names for the quadrilateral below.
Some examples:
quadrilateral ABCD
quadrilateral BCDA
quadrilateral CDAB
or
quadrilateral DABC
B
A
D
C
Quadrilaterals
consecutive or
Any two _______
vertices
sides of a quadrilateral are either __________
angles
nonconsecutive
_____________.
Q
P
S
R
Quadrilaterals
Segments that join nonconsecutive vertices of a quadrilateral are called
diagonals
________.
Q
P
R
P are
S and Q
nonconsecutive
vertices.
RP is a diagonal
SQ
S
R
Quadrilaterals
Name all pairs of consecutive sides:
QR and RS
RS and ST
ST and TQ
TQ and QR
Q
T
R
Name all pairs of nonconsecutive angles:
Q and S
T and R
S
Name the diagonals:
QS and TR
Quadrilaterals
A
Considering the quadrilateral to the right.
1
What shapes are formed if a diagonal
two triangles
is drawn? ___________
D
Use the Angle Sum Theorem (Section 5-2)
180
to find m1 + m2 + m3
3
4
2
B
5
Use the Angle Sum Theorem (Section 5-2)
180
to find m4 + m5 + m6
6
Find
m1 + m2 + m3
+ m4 + m5 + m6
180
+ 180
360
This leads to the following theorem.
C
Quadrilaterals
The sum of the measures of the angles of a quadrilateral is
360
____.
Theorem
8-1
a°
b°
a + b + c + d = 360
c°
d°
Quadrilaterals
Find the measure of B in quadrilateral ABCD if A = x, B = 2x,
C = x – 10, and D = 50.
mA + mB + mC + mD = 360
A
B
x + 2x + x – 10 + 50 = 360
4x + 40 = 360
4x = 320
C
x = 80
B = 2x
B = 2(80)
B = 160
D
Quadrilaterals
Parallelograms
You will learn to identify and use the properties of
parallelograms.
1) Parallelogram
Parallelograms
parallel sides
A parallelogram is a quadrilateral with two pairs of ____________.
In parallelogram ABCD below, DA || CB and
B
A
D
AB || DC
C
congruent
Also, the parallel sides are _________.
Knowledge gained about “parallels” (chapter 4)
will now be used in the following theorems.
Parallelograms
A
Theorem
8-2
Opposite angles of a
parallelogram are
congruent
________.
B
D
C
A  C
and
B  D
A
Theorem
8-3
Opposite sides of a
parallelogram are
congruent
________.
D
B
C
DA || CB, and AB || DC
Theorem
8-4
The consecutive
angles of a
parallelogram are
supplementary
____________.
A
D
B
C
mA + mB = 180
mD + mC = 180
Parallelograms
In
RSTU,
RS = 45, ST = 70, and U = 68.
S
R
Find:
45
RU = ____
70
Theorem 8-3
45
UT = _____
Theorem 8-3
68°
mS = _____
Theorem 8-2
112°
mT = _____
Theorem 8-4
70
U
68°
T
Parallelograms
The diagonals of a parallelogram ______
bisect each other.
A
AE  EC
Theorem
8-5
B
E
DE  EB
D
In
RSTU,
C
if RT = 56, find RE.
R
1
RT 
2
1
RE  56 
2
S
RE 
RE = 28
E
U
T
Parallelograms
In the figure below, ABCD is a parallelogram.
Since AD || BC and
diagonal DB is a transversal,
then ADB  CBD.
A
B
(Alternate Interior angles)
Since AB || DC and
diagonal DB is a transversal,
then BDC  DBA.
(Alternate Interior angles)
DB  BD
DBA  BDC
ASA Theorem
D
C
Parallelograms
A diagonal of a parallelogram separates it into two
congruent triangles
_________________.
A
Theorem
8-6
B
DBA  BDC
D
C
Parallelograms
The Escher design below is based on
parallelogram
a _____________.
You can use a parallelogram to make a simple
Escher-like drawing.
Change one side of the parallelogram and then
translate (slide) the change to the opposite side.
The resulting figure is used to make a design
with different colors and textures.
Parallelograms
Tests for Parallelograms
You will learn to identify and use tests to show that a
quadrilateral is a parallelogram.
Nothing New!
Tests for Parallelograms
If both pairs of opposite sides of a quadrilateral are
congruent then the quadrilateral is a parallelogram.
_________,
Theorem
8-7
A
D
B
C
AD  BC
and
AB  DC
Tests for Parallelograms
You can use the properties of congruent triangles and Theorem 8-7 to find
other ways to show that a quadrilateral is a parallelogram.
In quadrilateral PQRS, PR and QS bisect each
other at T.
P
Q
T
Show that PQRS is a parallelogram by
providing a reason for each step.
S
PT  TR and QT  TS
Definition of segment bisector
PTQ  RTS and STP  QTR
PQT  RST and PTS  RTQ
PQ  RS and PS  RQ
PQRS
R
Vertical angles are congruent
SAS
Corresp. parts of Congruent Triangles are Congruent
is a parallelog ram
Theorem 8-7
Tests for Parallelograms
parallel and
If one pair of opposite sides of a quadrilateral is _______
congruent then the quadrilateral is a parallelogram.
_________,
A
B
Theorem
8-8
C
D
AB || DC
AB  DC
Tests for Parallelograms
bisect each other
If the diagonals of a quadrilateral ________________,
then the quadrilateral is a parallelogram.
A
Theorem
8-9
B
E
D
AE  EC
C
DE  EB
Tests for Parallelograms
Determine whether each quadrilateral is a parallelogram.
If the figure is a parallelogram, give a reason for your answer.
A
D
B
AB  DC
Given
AB || DC
Alt. Int. Angles
C
Therefore, quadrilateral ABCD is a parallelogram.
Theorem 8-8
Tests for Parallelograms
Rectangles, Rhombi, and Squares
You will learn to identify and use the properties of rectangles,
rhombi, and squares.
1) Rectangle
2) Rhombus
3) Square
Rectangles, Rhombi, and Squares
A closed figure,
Quadrilateral
4 sides
& 4 vertices
Opposite
sides parallel
Parallelogram
opposite sides congruent
Parallelogram with
Rhombus
4 congruent sides
Parallelogram with
Rectangle
4 right angles
Parallelogram
with
Squaresides
4 congruent
and
4 right angles
Rectangles, Rhombi, and Squares
Identify the parallelogram
below.
A
B
D
C
Parallelogram ABCD has
4 right angles, but the four
sides are not congruent.
Therefore, it is a
_________
rectangle
Identify the parallelogram
below.
rhombus
Rectangles, Rhombi, and Squares
The diagonals of a rectangle are _________.
congruent
A
B
D
C
Theorem
8-10
AC  DB
Rectangles, Rhombi, and Squares
perpendicular
The diagonals of a rhombus are ____________.
B
A
Theorem
8-11
C
D
AC  DB
Rectangles, Rhombi, and Squares
bisects a pair of opposite angles.
Each diagonal of a rhombus _______
1A 2
1
2
7  8
D
Theorem
8-12
8
7
6
5
3
4
3B 4
C5
 6
Rectangles, Rhombi, and Squares
Use square XYZW to answer the following questions:
1) If YW = 14,
14
XZ = ____
A square has all the properties of a
rectangle, and the diagonals of a
rectangle are congruent.
Y
X
O
90
2) mYOX = ____
A square has all the properties of a
rhombus, and the diagonals of a
rhombus are perpendicular.
W
Z
3) Name all segments that are congruent to WO. Explain your reasoning.
OY, XO, and OZ
The diagonals are congruent and they bisect
each other.
Rectangles, Rhombi, and Squares
Use the Venn diagram to answer the following questions: T or F
Quadrilaterals
Parallelograms
Rhombi
Squares
T
1) Every square is a rhombus: ___
F
2) Every rhombus is a square: ___
F
3) Every rectangle is a square: ___
T
4) Every square is a rectangle: ___
Rectangles
5) All rhombi are
T
parallelograms: ___
6) Every parallelogram
F
is a rectangle: ___
Rectangles, Rhombi, and Squares
Trapezoids
You will learn to identify and use the properties of trapezoids
and isosceles trapezoids.
1) Trapezoid
Trapezoids
parallel sides
quadrilateral with exactly one pair of ____________.
A trapezoid is a ____________
bases
The parallel sides are called ______.
legs
The non parallel sides are called _____.
T
Each trapezoid has two pair of
base angles.
leg
T and R are one pair
of base angles.
P and A are the other
pair of base angles.
P
base
base angles
base
R
leg
A
Trapezoids
The median of a trapezoid is parallel to the _____,
bases
and the length of the median equals _______________
one-half the sum of
the lengths of the bases.
A
B
Theorem
8-13
N
M
D
C
AB || MN ,
DC || MN
1
MN   AB  DC 
2
Trapezoids
Find the length of median MN in trapezoid ABCD if
AB = 16 and DC = 20
1
MN   AB  DC 
2
1
MN  16  20 
2
1
MN  36 
2
MN  18
16
A
M
D
18
20
B
N
C
Trapezoids
If the legs of a trapezoid are congruent, the trapezoid is an
_________________.
isosceles trapezoid
In lesson 6 – 4, you learned that the base angles of an isosceles triangle are
congruent.
There is a similar property of isosceles trapezoids.
Trapezoids
Each pair of __________
base angles in an isosceles trapezoid is congruent.
W
X
W  X
Theorem
8-14
Z  Y
Z
Y
Trapezoids
Find the missing angle measures in isosceles trapezoid TRAP.
T
Theorem 8 – 14
P  A
120°
120°
R
mP = mA
60 = mA
T  R
Theorem 8 – 14
P + A + 2(T) = 360
60 + 60 + 2(T) = 360
120 + 2(T) = 360
2(T) = 240
T = 120
R = 120
P
60°
60°
A
Trapezoids