Exotic spheres and curvature - American Mathematical Society
... five, any smooth manifold with the homotopy type of a sphere must be homeomorphic to a sphere. This is the Generalised Poincaré Conjecture, proved by Smale in [Sm1]. Thus in these dimensions the set of diffeomorphism classes of homotopy spheres is precisely the union of the diffeomorphism class of the ...
... five, any smooth manifold with the homotopy type of a sphere must be homeomorphic to a sphere. This is the Generalised Poincaré Conjecture, proved by Smale in [Sm1]. Thus in these dimensions the set of diffeomorphism classes of homotopy spheres is precisely the union of the diffeomorphism class of the ...
Axioms of Incidence Geometry Incidence Axiom 1. There exist at
... Theorem 4.30 (Constructing a Perpendicular). Let ` be a line and let P be a point on `. Then there exists a unique line m that is perpendicular to ` at P . Theorem 5.1 (Consistency of Triangle Vertices). If 4ABC is a triangle, the only extreme points of 4ABC are A, B, and C . Thus if 4ABC D 4A0 B 0 ...
... Theorem 4.30 (Constructing a Perpendicular). Let ` be a line and let P be a point on `. Then there exists a unique line m that is perpendicular to ` at P . Theorem 5.1 (Consistency of Triangle Vertices). If 4ABC is a triangle, the only extreme points of 4ABC are A, B, and C . Thus if 4ABC D 4A0 B 0 ...
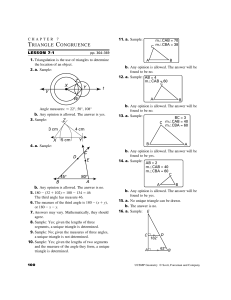
Key Concepts, continued Vertical angles
... Key Concepts, continued Theorem Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, then that point is equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then the point lies on the perpendicular bisector o ...
... Key Concepts, continued Theorem Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, then that point is equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then the point lies on the perpendicular bisector o ...
Symplectic structures -- a new approach to geometry.
... motion can be put in Hamiltonian form and that symplectic properties can be exploited to solve these equations in certain important cases. Therefore, because symplectic structures are built into the classical theory they are very important in the new deformed theories. In “classical” symplectic geom ...
... motion can be put in Hamiltonian form and that symplectic properties can be exploited to solve these equations in certain important cases. Therefore, because symplectic structures are built into the classical theory they are very important in the new deformed theories. In “classical” symplectic geom ...
Key Concepts, continued
... that can be proven true by given, definitions, postulates, or already proven theorems •Postulate: a statement that describes a fundamental relationship between basic terms of geometry. Postulates are accepted as true without proof. •Conjecture: an educated guess based on known information 1.8.1: Pro ...
... that can be proven true by given, definitions, postulates, or already proven theorems •Postulate: a statement that describes a fundamental relationship between basic terms of geometry. Postulates are accepted as true without proof. •Conjecture: an educated guess based on known information 1.8.1: Pro ...
Hyperbolic Geometry and 3-Manifold Topology
... If instead, |∂M | < ∞, prove the above result where C is a relative core. Remark 1.14. A consequence of the above exercise is that if E is an end of M , then E is homeomorphic to the unique end of a 1-ended submanifold ME of M . We will often abuse notation by referring to an end of a 3-manifold wit ...
... If instead, |∂M | < ∞, prove the above result where C is a relative core. Remark 1.14. A consequence of the above exercise is that if E is an end of M , then E is homeomorphic to the unique end of a 1-ended submanifold ME of M . We will often abuse notation by referring to an end of a 3-manifold wit ...
8 Similarity - Big Ideas Learning
... RELATIONSHIPS When two similar polygons have a scale factor of k, the ratio of their areas is equal to k2. ...
... RELATIONSHIPS When two similar polygons have a scale factor of k, the ratio of their areas is equal to k2. ...
Identifying Congruent Figures
... Theorem 4.3 Third Angles Theorem If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. If A D and B E, then C F. ...
... Theorem 4.3 Third Angles Theorem If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. If A D and B E, then C F. ...
Course Notes for MA 460. Version 5.
... in physics were tested by thousands of observations over almost 200 years, but the small uncertainties in these observations concealed the fact that there is a more accurate and fundamental theory than Newton’s, namely Einstein’s theory of relativity. Mathematics is the only science in which there i ...
... in physics were tested by thousands of observations over almost 200 years, but the small uncertainties in these observations concealed the fact that there is a more accurate and fundamental theory than Newton’s, namely Einstein’s theory of relativity. Mathematics is the only science in which there i ...
Notes - WVU Math Department
... If f : ` → R is as in Axiom 2, then f is called coordinate system for ` and f (P ) is a coordinate of P on ` (with respect to f ). The axiom insures that each line contains many points. Go over Theorem 6.6, with proof. Written assignment for Monday, January 26: Ex 1: (Ex. 6.6) Show that Axioms 1 and ...
... If f : ` → R is as in Axiom 2, then f is called coordinate system for ` and f (P ) is a coordinate of P on ` (with respect to f ). The axiom insures that each line contains many points. Go over Theorem 6.6, with proof. Written assignment for Monday, January 26: Ex 1: (Ex. 6.6) Show that Axioms 1 and ...
Chapter 6 Power Point Slides File
... Find the value of x and y. Then find the value of each line segment ...
... Find the value of x and y. Then find the value of each line segment ...
[edit] Construction of the Lebesgue measure
... [edit] Intuition The intuitive dimension of a geometric object is the number of independent parameters you need to pick out a unique point inside. But you can easily take a single real number, one parameter, and split its digits to make two real numbers. The example of a space-filling curve shows th ...
... [edit] Intuition The intuitive dimension of a geometric object is the number of independent parameters you need to pick out a unique point inside. But you can easily take a single real number, one parameter, and split its digits to make two real numbers. The example of a space-filling curve shows th ...
The Postulates of Neutral Geometry Axiom 1 (The Set Postulate
... The Postulates of Neutral Geometry Axiom 1 (The Set Postulate). Every line is a set of points, and the collection of all points forms a set P called the plane. Axiom 2 (The Existence Postulate). There exist at least two distinct points. Axiom 3 (The Incidence Postulate). For every pair of distinct p ...
... The Postulates of Neutral Geometry Axiom 1 (The Set Postulate). Every line is a set of points, and the collection of all points forms a set P called the plane. Axiom 2 (The Existence Postulate). There exist at least two distinct points. Axiom 3 (The Incidence Postulate). For every pair of distinct p ...
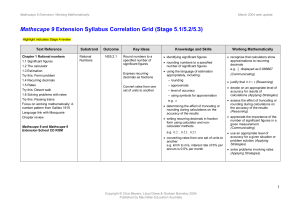
View - Macmillan Publishers
... check expansions and factorisations by performing the reverse process (Reasoning) interpret statements involving algebraic symbols in other contexts e.g. spreadsheets (Communicating) solve problems, such as: find a relationship that describes the number of diagonals in a polygon with n sides ( ...
... check expansions and factorisations by performing the reverse process (Reasoning) interpret statements involving algebraic symbols in other contexts e.g. spreadsheets (Communicating) solve problems, such as: find a relationship that describes the number of diagonals in a polygon with n sides ( ...
Slide 1
... parallel sides A parallelogram is a quadrilateral with two pairs of ____________. In parallelogram ABCD below, DA || CB and ...
... parallel sides A parallelogram is a quadrilateral with two pairs of ____________. In parallelogram ABCD below, DA || CB and ...















![[edit] Construction of the Lebesgue measure](http://s1.studyres.com/store/data/001141507_1-534aa5aeea25b32a8226835f0ebc16e0-300x300.png)