Ruler Postulate: The points on a line can be matched one to one
... Ruler Postulate: The points on a line can be matched one to one with the ...
... Ruler Postulate: The points on a line can be matched one to one with the ...
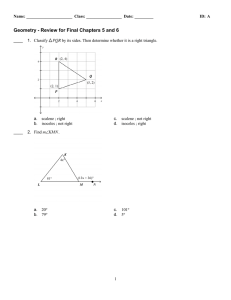
ExamView - geometry review for final chapters 5 and 6 .tst
... 42. Using the Midpoint Formula, M ÁÁÁÁ 0, ˜˜˜˜ and P ÁÊË 2n,0 ˜ˆ¯ . Using the Distance Formula, MP = and BC = 5n . ...
... 42. Using the Midpoint Formula, M ÁÁÁÁ 0, ˜˜˜˜ and P ÁÊË 2n,0 ˜ˆ¯ . Using the Distance Formula, MP = and BC = 5n . ...
1. Postulate 11 Through any two points there is exactly one line 2
... Postulate 12 If two lines intersect, then they intersect in exactly one point Postulate 13 If two planes intersect, then they intersect in exactly one line Postulate 14 Through any three noncollinear points there is exactly one plane Formula The Distance Formula: The distance d between two poi ...
... Postulate 12 If two lines intersect, then they intersect in exactly one point Postulate 13 If two planes intersect, then they intersect in exactly one line Postulate 14 Through any three noncollinear points there is exactly one plane Formula The Distance Formula: The distance d between two poi ...
1.7 The Formal Proof of a Theorem
... If a person lives in London, then that person lives in England. ...
... If a person lives in London, then that person lives in England. ...
PowerPoint 簡報 - Browser Express
... 1. Two figures having the same shape are called similar figures. The figures A and B as shown is an example of similar figures. 2. Two congruent figures must be also similar figures. 3. When a figure is enlarged or reduced, the new figure is similar to the original one. Index 11.3 ...
... 1. Two figures having the same shape are called similar figures. The figures A and B as shown is an example of similar figures. 2. Two congruent figures must be also similar figures. 3. When a figure is enlarged or reduced, the new figure is similar to the original one. Index 11.3 ...
File - IGCSE/O
... 1. Two figures having the same shape are called similar figures. The figures A and B as shown is an example of similar figures. 2. Two congruent figures must be also similar figures. 3. When a figure is enlarged or reduced, the new figure is similar to the original one. Index 11.3 ...
... 1. Two figures having the same shape are called similar figures. The figures A and B as shown is an example of similar figures. 2. Two congruent figures must be also similar figures. 3. When a figure is enlarged or reduced, the new figure is similar to the original one. Index 11.3 ...
EPH-classifications in Geometry, Algebra, Analysis and Arithmetic
... distribution F⊥ , orthogonal to F, is evidently integrable. In arbitrary codimension complicacies arise and the simplest case these can be well treated in case of 2-dimensional foliations on 4-manifolds.(Cairns and Ghys 1986) Assuming that the foliation F and manifold M are oriented and C ∞ . In gen ...
... distribution F⊥ , orthogonal to F, is evidently integrable. In arbitrary codimension complicacies arise and the simplest case these can be well treated in case of 2-dimensional foliations on 4-manifolds.(Cairns and Ghys 1986) Assuming that the foliation F and manifold M are oriented and C ∞ . In gen ...
Right Angles Congruence Theorem
... If angles 1 and 3 are supplementary and angles 5 and 3 are supplementary, then angles 1 and 5 are congruent. ...
... If angles 1 and 3 are supplementary and angles 5 and 3 are supplementary, then angles 1 and 5 are congruent. ...
Proving Triangle Similarity by SSS and SAS 8.3
... similar? Is this true for each pair of triangles that are not similar? f. Make a conjecture about the similarity of two triangles based on their ...
... similar? Is this true for each pair of triangles that are not similar? f. Make a conjecture about the similarity of two triangles based on their ...
Essential Question
... b. Copy the table and complete column 1. c. Are the triangles similar? Explain your reasoning. d. Repeat parts (a)–(c) for columns 2–6 in the table. e. How are the corresponding side lengths related in each pair of triangles that are similar? Is this true for each pair of triangles that are not simi ...
... b. Copy the table and complete column 1. c. Are the triangles similar? Explain your reasoning. d. Repeat parts (a)–(c) for columns 2–6 in the table. e. How are the corresponding side lengths related in each pair of triangles that are similar? Is this true for each pair of triangles that are not simi ...
Theorems List - bonitz-geo
... Theorem 6-8 (Quadrilateral’s Opposite Angles) If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 6-9 (Rhombuses Diagonals) Each diagonal of a rhombus bisects two angles of the rhombus Theorem 6-10 (Rhombuses Diagonals) The diagonals ...
... Theorem 6-8 (Quadrilateral’s Opposite Angles) If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 6-9 (Rhombuses Diagonals) Each diagonal of a rhombus bisects two angles of the rhombus Theorem 6-10 (Rhombuses Diagonals) The diagonals ...
Theorems List - bonitz-geo
... Theorem 6-8 (Quadrilateral’s Opposite Angles) If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 6-9 (Rhombuses Diagonals) Each diagonal of a rhombus bisects two angles of the rhombus Theorem 6-10 (Rhombuses Diagonals) The diagonals ...
... Theorem 6-8 (Quadrilateral’s Opposite Angles) If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 6-9 (Rhombuses Diagonals) Each diagonal of a rhombus bisects two angles of the rhombus Theorem 6-10 (Rhombuses Diagonals) The diagonals ...
Consequences of the Euclidean Parallel Postulate
... Corollary H2.8. In any triangle, the sum of the measures of any two angles is less than 180◦ . Proof. Since the measures of all three angles sum to 180◦, and the measure of each angle is positive, the sum of any two of them must be strictly less than 180◦ . Corollary H2.9. In any triangle, at least ...
... Corollary H2.8. In any triangle, the sum of the measures of any two angles is less than 180◦ . Proof. Since the measures of all three angles sum to 180◦, and the measure of each angle is positive, the sum of any two of them must be strictly less than 180◦ . Corollary H2.9. In any triangle, at least ...
pdf copy of pages used to make lesson.
... Theorem 52: A segment joining the midpoints of two sides of a triangle is parallel to the third side, and its length is one-half the length of the third side. (Midline Theorem) B D ...
... Theorem 52: A segment joining the midpoints of two sides of a triangle is parallel to the third side, and its length is one-half the length of the third side. (Midline Theorem) B D ...
Geometry 4.5
... B, and the fire form a triangle. The dispatcher knows the distance from tower A to tower B and the measures of A and B. So, the measures of two angles and an included side of the triangle are known. By the ASA Congruence Postulate, all triangles with these measures are congruent. So, the triangle fo ...
... B, and the fire form a triangle. The dispatcher knows the distance from tower A to tower B and the measures of A and B. So, the measures of two angles and an included side of the triangle are known. By the ASA Congruence Postulate, all triangles with these measures are congruent. So, the triangle fo ...
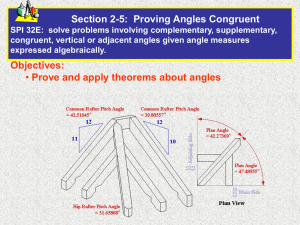
Section 2-8 - winegardnermathclass
... Proving Angle Relationships After today’s lesson you should be able to: - Write proofs involving supplementary and complementary angles. - Write proofs involving congruent and right angles. Review: Supplementary angles add up to 180. Complementary angles add up to 90. Congruent angles have the same ...
... Proving Angle Relationships After today’s lesson you should be able to: - Write proofs involving supplementary and complementary angles. - Write proofs involving congruent and right angles. Review: Supplementary angles add up to 180. Complementary angles add up to 90. Congruent angles have the same ...
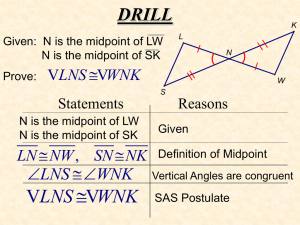
Slide 1 - NEHSMath
... If two angles are complements of the same angle (or of congruent angles), then the two angles are congruent. Given: 1 and 2 are complementary 3 and 2 are complementary Prove: 1 3 STATEMENT 1 and 2 are complementary 3 and 2 are complementary ...
... If two angles are complements of the same angle (or of congruent angles), then the two angles are congruent. Given: 1 and 2 are complementary 3 and 2 are complementary Prove: 1 3 STATEMENT 1 and 2 are complementary 3 and 2 are complementary ...
Name
... Theorem 2.4 Congruent Supplements Theorem: If two angles are supplementary to the same angle (or to congruent angles), then they are congruent. Theorem 2.5 Congruent Complements Theorem: If two angles are complementary to the same angle (or to congruent angles), then they are congruent. Postulate 12 ...
... Theorem 2.4 Congruent Supplements Theorem: If two angles are supplementary to the same angle (or to congruent angles), then they are congruent. Theorem 2.5 Congruent Complements Theorem: If two angles are complementary to the same angle (or to congruent angles), then they are congruent. Postulate 12 ...
Regular Hypersurfaces, Intrinsic Perimeter and Implicit Function
... If p, q ∈ G, their cc-distance dc (p, q) is dc (p, q) = inf {T > 0 : γ : [0, T ] → G is subunit, γ(0) = p, γ(T ) = q} . (2) The fact, that under assumption (1), dc (p, q) is finite for any p, q is the content of Chow theorem (see e.g. [6] or [28]). We recall that the topology induced on Rn by dc is t ...
... If p, q ∈ G, their cc-distance dc (p, q) is dc (p, q) = inf {T > 0 : γ : [0, T ] → G is subunit, γ(0) = p, γ(T ) = q} . (2) The fact, that under assumption (1), dc (p, q) is finite for any p, q is the content of Chow theorem (see e.g. [6] or [28]). We recall that the topology induced on Rn by dc is t ...