Name: TP: ____ CRS PPF 601 – Apply properties of 30-60
... SUT VUW by the ________________________________. The diagram shows that STU _________ , so by the Third Angles Theorem, S _________. By the Triangle Sum Theorem, mS = __________________ = _______. So, mS mV = _______ by the definition of congruent angles. 8) Find the value of the indi ...
... SUT VUW by the ________________________________. The diagram shows that STU _________ , so by the Third Angles Theorem, S _________. By the Triangle Sum Theorem, mS = __________________ = _______. So, mS mV = _______ by the definition of congruent angles. 8) Find the value of the indi ...
Symplectic Topology
... geometry is very special. For instance, R 2n has a unique smooth structure if n 6= 2, but R 4 has uncountably many. In the world of closed simply-connected manifolds, in a given homeomorphism type in dimension k 6= 4 there are at most finitely many diffeomorphism types – and (complicated) homotopy i ...
... geometry is very special. For instance, R 2n has a unique smooth structure if n 6= 2, but R 4 has uncountably many. In the world of closed simply-connected manifolds, in a given homeomorphism type in dimension k 6= 4 there are at most finitely many diffeomorphism types – and (complicated) homotopy i ...
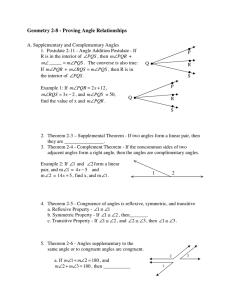
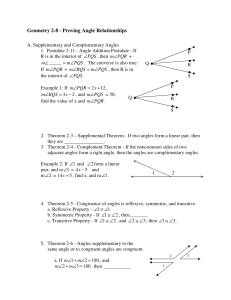
Geometry 2-8 - Proving Angle Relationships
... R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: If m∠PQR = 2 x + 12 , m∠RQS = 3x − 2 , and m∠PQS = 50, find the value of x and m∠PQR . ...
... R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: If m∠PQR = 2 x + 12 , m∠RQS = 3x − 2 , and m∠PQS = 50, find the value of x and m∠PQR . ...
Concepts 12-16 Notes Triangle Relationships and Similar Triangles
... Concept 15 – Ratios and Proportions (Section 7.1) ...
... Concept 15 – Ratios and Proportions (Section 7.1) ...
Geometry. “Direct” and “Inverse” Theorems. Ceva`s
... is actually often the case that the proof of the necessary condition, AB, i. e. the “inverse” theorem, is much simpler than the proof of the “direct” proposition, establishing the sufficiency, A B. It often could be achieved by using the sufficiency condition which has already been proven, and em ...
... is actually often the case that the proof of the necessary condition, AB, i. e. the “inverse” theorem, is much simpler than the proof of the “direct” proposition, establishing the sufficiency, A B. It often could be achieved by using the sufficiency condition which has already been proven, and em ...
File
... Given ray AB and a number r between 0 and 180, there is exactly one ray with endpoint A extending on either side of ray AB, such that the measure of the angle formed is r. ...
... Given ray AB and a number r between 0 and 180, there is exactly one ray with endpoint A extending on either side of ray AB, such that the measure of the angle formed is r. ...
2.7.3 Elliptic Parallel Postulate
... Birkhoff's axioms. The incidence axiom that "any two points determine a unique line," needs to be modified to read "any two points determine at least one line." Hilbert's Axioms of Order (betweenness of points) may be replaced with axioms of separation that give the properties of how points of a lin ...
... Birkhoff's axioms. The incidence axiom that "any two points determine a unique line," needs to be modified to read "any two points determine at least one line." Hilbert's Axioms of Order (betweenness of points) may be replaced with axioms of separation that give the properties of how points of a lin ...
Chapter 9 - SchoolNotes.com
... Angle-Angle Similarity Postulate (AA~): If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Side-Angle-Side Similarity Theorem (SAS~): If an angle of one triangle is congruent to an angle of another triangle, and the sides including the angl ...
... Angle-Angle Similarity Postulate (AA~): If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Side-Angle-Side Similarity Theorem (SAS~): If an angle of one triangle is congruent to an angle of another triangle, and the sides including the angl ...
Definition 2 - math.uh.edu
... The Formal Proof of a Theorem. Indirect Proof. Definition 1: The hypothesis (H) of a statement describes given situation. The conclusion (C) describes what you need to establish or prove. Some theorems are worded in the form “If H, then C”, where H is the hypothesis and C is the conclusion. In some ...
... The Formal Proof of a Theorem. Indirect Proof. Definition 1: The hypothesis (H) of a statement describes given situation. The conclusion (C) describes what you need to establish or prove. Some theorems are worded in the form “If H, then C”, where H is the hypothesis and C is the conclusion. In some ...
Untitled
... The Formal Proof of a Theorem. Indirect Proof. Definition 1: The hypothesis (H) of a statement describes given situation. The conclusion (C) describes what you need to establish or prove. Some theorems are worded in the form “If H, then C”, where H is the hypothesis and C is the conclusion. In some ...
... The Formal Proof of a Theorem. Indirect Proof. Definition 1: The hypothesis (H) of a statement describes given situation. The conclusion (C) describes what you need to establish or prove. Some theorems are worded in the form “If H, then C”, where H is the hypothesis and C is the conclusion. In some ...
Congruence in Right Triangles
... Right triangles provide a special case for congruence. There is an SSA congruence rule. It occurs when the hypotenuses are congruent and one pair of legs are congruent. ...
... Right triangles provide a special case for congruence. There is an SSA congruence rule. It occurs when the hypotenuses are congruent and one pair of legs are congruent. ...
MA 501 Homework #8
... pdf files. I have prepared a summary, giving the sequence of results, but no proofs; see http://www.ms.uky.edu/∼lee/ma341fa12/smsg.pdf. The idea is that any theorem in this list can be proved using only the preceding results. Study the proofs of the following theorems (some of the proofs are to be f ...
... pdf files. I have prepared a summary, giving the sequence of results, but no proofs; see http://www.ms.uky.edu/∼lee/ma341fa12/smsg.pdf. The idea is that any theorem in this list can be proved using only the preceding results. Study the proofs of the following theorems (some of the proofs are to be f ...
4-2 - Midland ISD
... midsegments, and medians, and apply these relationships to solve problems. ...
... midsegments, and medians, and apply these relationships to solve problems. ...
3-1 Parallel Lines and Transversals
... Warm-ups – Complete Slide below – Check in and discuss A#3.1 ...
... Warm-ups – Complete Slide below – Check in and discuss A#3.1 ...
Solutions to suggested problems.
... conclude NOT s, and backtrack a bit - combining ¬ s with r∨s through disjunctive syllogism simply means that r is no longer just an assumption, but an established result ... leading in turn to q. Had I noticed in advance that s was going to blow up, I could have shortened the proof a bit by ...
... conclude NOT s, and backtrack a bit - combining ¬ s with r∨s through disjunctive syllogism simply means that r is no longer just an assumption, but an established result ... leading in turn to q. Had I noticed in advance that s was going to blow up, I could have shortened the proof a bit by ...
2.5.1 Supplement Postulate
... theorem for most high school geometry courses. The proof that the Supplement Postulate is not independent is given below; Exercise 2.43 asks the reader to provide the reasons for each step of the proof. Theorem 2.8 (Vertical Angle Theorem) Vertical angles are congruent. The next theorem, called the ...
... theorem for most high school geometry courses. The proof that the Supplement Postulate is not independent is given below; Exercise 2.43 asks the reader to provide the reasons for each step of the proof. Theorem 2.8 (Vertical Angle Theorem) Vertical angles are congruent. The next theorem, called the ...
2.6.1 Parallel Lines without a Parallel Postulate
... Given line AB, line DE, and line BE such that A-B-C, D-E-F, and G-B-E-H where A and D on the same side of line BE, then line BE is called a transversal. Angles and (also and ) are called alternate interior angles. The next theorem will be useful in proving two lines are parallel. From your high scho ...
... Given line AB, line DE, and line BE such that A-B-C, D-E-F, and G-B-E-H where A and D on the same side of line BE, then line BE is called a transversal. Angles and (also and ) are called alternate interior angles. The next theorem will be useful in proving two lines are parallel. From your high scho ...
FINITENESS OF RANK INVARIANTS OF MULTIDIMENSIONAL
... this functional setting is not large enough to address the problems encountered in practical applications, and stability of persistence diagrams is revisited. The basic assumption to prove stability in [5] is the finiteness of persistent homology ranks, but the question of how achieving this is left ...
... this functional setting is not large enough to address the problems encountered in practical applications, and stability of persistence diagrams is revisited. The basic assumption to prove stability in [5] is the finiteness of persistent homology ranks, but the question of how achieving this is left ...