* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download What is an Evolutionary Algorithm?
Hardy–Weinberg principle wikipedia , lookup
Genome (book) wikipedia , lookup
Dual inheritance theory wikipedia , lookup
Human genetic variation wikipedia , lookup
Inbreeding avoidance wikipedia , lookup
Deoxyribozyme wikipedia , lookup
Frameshift mutation wikipedia , lookup
Point mutation wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Genetic drift wikipedia , lookup
Koinophilia wikipedia , lookup
Gene expression programming wikipedia , lookup
Group selection wikipedia , lookup
Machine Learning
Evolutionary Algorithms
Universe
Borg
Vogons
Art
Life Sciences
etc
Biotop
Society
Stones & Seas
etc
Science
Politics
Sports
etc
Social Sciences
Mathematics
Earth
Exact Sciences
etc
Physics
Computer Science
etc
Software Engineering
Computational Intelligence
etc
You are here
Neural Nets
Evolutionary Computing
Fuzzy Systems
What is Evolutionary Computation?
An abstraction from the theory of
biological evolution that is used to
create optimization procedures or
methodologies, usually implemented
on computers, that are used to solve
problems.
Brief History : the ancestors
• 1948, Turing:
proposes “genetical or evolutionary search”
• 1962, Bremermann
optimization through evolution and recombination
• 1964, Rechenberg
introduces evolution strategies
• 1965, L. Fogel, Owens and Walsh
introduce evolutionary programming
• 1975, Holland
introduces genetic algorithms
• 1992, Koza
introduces genetic programming
Darwinian Evolution
Survival of the fittest
All environments have finite resources
(i.e., can only support a limited number of individuals)
Life forms have basic instinct/ lifecycles geared towards
reproduction
Therefore some kind of selection is inevitable
Those individuals that compete for the resources most
effectively have increased chance of reproduction
Note: fitness in natural evolution is a derived, secondary
measure, i.e., we (humans) assign a high fitness to
individuals with many offspring
Darwinian Evolution:Summary
Population consists of diverse set of individuals
Combinations of traits that are better adapted tend to
increase representation in population
Individuals are “units of selection”
Variations occur through random changes yielding
constant source of diversity, coupled with selection
means that:
Population is the “unit of evolution”
Note the absence of “guiding force”
The Concept of Natural Selection
Limited number of resources
Competition results in struggle for existence
Success depends on fitness -
fitness of an individual: how well-adapted an individual is
to their environment. This is determined by their genes
(blueprints for their physical and other characteristics).
Successful individuals are able to reproduce
and pass on their genes
Crossing-over
Chromosome pairs align and duplicate
Inner pairs link at a centromere and swap parts of
themselves
After
crossing-over one of each pair goes into each
gamete
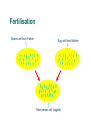
Recombination (Crossing-Over)
Image from http://esg-www.mit.edu:8001/bio/mg/meiosis.html
Fertilisation
Sperm cell from Father
Egg cell from Mother
New person cell (zygote)
Mutation
Occasionally some of the genetic material changes
very slightly during this process (replication error)
This means that the child might have genetic material
information not inherited from either parent
This can be
– catastrophic: offspring in not viable (most likely)
– neutral: new feature not influences fitness
– advantageous: strong new feature occurs
Redundancy in the genetic code forms a good way of
error checking
Genetic code
• All proteins in life on earth are composed of sequences
built from 20 different amino acids
• DNA is built from four nucleotides in a double helix
spiral: purines A,G; pyrimidines T,C
• Triplets of these from codons, each of which codes for
a specific amino acid
• Much redundancy:
•
•
•
•
purines complement pyrimidines
the DNA contains much rubbish
43=64 codons code for 20 amino acids
genetic code = the mapping from codons to amino acids
• For all natural life on earth, the genetic code is the
same !
Motivations for Evolutionary Computation
The best problem solver known in nature is:
–
the (human) brain that created “the wheel, New York,
wars and so on” (after Douglas Adams’ Hitch-Hikers
Guide)
–
the evolution mechanism that created the human brain
(after Darwin’s Origin of Species)
Answer 1 neurocomputing
Answer 2 evolutionary computing
Problem type 1 : Optimisation
We have a model of our system and seek inputs that
give us a specified goal
e.g.
time tables for university, call center, or hospital
– design specifications, etc etc
–
EC
A population of individuals exists in an environment with
limited resources
Competition for those resources causes selection of those
fitter individuals that are better adapted to the environment
These individuals act as seeds for the generation of new
individuals through recombination and mutation
The new individuals have their fitness evaluated and
compete (possibly also with parents) for survival.
Over time Natural selection causes a rise in the fitness of
the population
General Scheme of EAs
Pseudo-code for typical EA
What are the different types of EAs
Historically different flavours of EAs have
been associated with different
representations:
Binary strings : Genetic Algorithms
– Real-valued vectors : Evolution Strategies
– Trees: Genetic Programming
– Finite state Machines: Evolutionary
Programming
–
Evolutionary Algorithms
Parameters of EAs may differ from one type to
another. Main parameters:
–
–
–
–
–
Population size
Maximum number of generations
Elitism factor
Mutation rate
Cross-over rate
There are six main characteristics of EAs
–
–
–
–
–
–
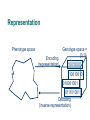
Representation
Selection
Recombination
Mutation
Fitness Function
Survivor Decision
19
Example: Discrete Representation (Binary
alphabet)
Representation of an individual can be using discrete values (binary,
integer, or any other system with a discrete set of values).
Following is an example of binary representation.
CHROMOSOME
GENE
Evaluation (Fitness) Function
Represents the requirements that the population should
adapt to
Called also quality function or objective function
Assigns a single real-valued fitness to each phenotype
which forms the basis for selection
–
So the more discrimination (different values) the better
Typically we talk about fitness being maximised
–
Some problems may be best posed as minimisation
problems
Population
Holds (representations of) possible solutions
Usually has a fixed size and is a multiset of genotypes
Some sophisticated EAs also assert a spatial structure on
the population e.g., a grid.
Selection operators usually take whole population into
account i.e., reproductive probabilities are relative to current
generation
Parent Selection Mechanism
Assigns variable probabilities of individuals acting as
parents depending on their fitness
Usually probabilistic
–
high quality solutions more likely to become parents than
low quality
–
but not guaranteed
–
even worst in current population usually has non-zero
probability of becoming a parent
Variation Operators
Role is to generate new candidate solutions
There has been much debate about relative importance of
recombination and mutation
–
Nowadays most EAs use both
–
Choice of particular variation operators is representation
dependant
Mutation
Acts on one genotype and delivers another
Element of randomness is essential and differentiates it
from other unary heuristic operators
May guarantee connectedness of search space and hence
convergence proofs
Recombination
Merges information from parents into offspring
Choice of what information to merge is stochastic
Most offspring may be worse, or the same as the
parents
Hope is that some are better by combining elements of
genotypes that lead to good traits
Survivor Selection
replacement
Most EAs use fixed population size so need a way of going
from (parents + offspring) to next generation
Often deterministic
– Fitness based : e.g., rank parents+offspring and take
best
– Age based: make as many offspring as parents and
delete all parents
Sometimes do combination
Example: Fitness proportionate selection
Expected number of times fi is selected for
mating is: f i f
Better (fitter) individuals
have:
more space
more chances to be
selected
Best
Worst
Example: Tournament selection
Select k random individuals, without
replacement
Take the best
–
k is called the size of the tournament
Example: Ranked based selection
Individuals are sorted on their fitness value
from best to worse. The place in this sorted list
is called rank.
Instead of using the fitness value of an
individual, the rank is used by a function to
select individuals from this sorted list. The
function is biased towards individuals with a
high rank (= good fitness).
Example: Ranked based selection
Fitness: f(A) = 5, f(B) = 2, f(C) = 19
Rank: r(A) = 2, r(B) = 3, r(C) = 1
(r ( x) 1)
h( x) min (max min)
n 1
Function: h(A) = 3, h(B) = 5, h(C) = 1
Proportion on the roulette wheel:
p(A) = 11.1%, p(B) = 33.3%, p(C) = 55.6%
*skip*
Initialisation / Termination
Initialisation usually done at random,
–
Need to ensure even spread and mixture of possible allele values
–
Can include existing solutions, or use problem-specific heuristics, to
“seed” the population
Termination condition checked every generation
–
Reaching some (known/hoped for) fitness
–
Reaching some maximum allowed number of generations
–
Reaching some minimum level of diversity
–
Reaching some specified number of generations without fitness
improvement
Algorithm performance
Never draw any conclusion from a single run
–
–
use statistical measures (averages, medians)
from a sufficient number of independent runs
From the application point of view
–
–
design perspective:
find a very good solution at least once
production perspective:
find a good solution at almost every run
Example: the 8 queens problem
Place 8 queens on an 8x8 chessboard in
such a way that they cannot check each other
The 8 queens problem: representation
Phenotype:
a board configuration
Genotype:
a permutation of
the numbers 1 - 8
Obvious mapping
1 3 5 2 6 4 7 8
8 Queens Problem: Fitness evaluation
• Penalty of one queen:
the number of queens she can check.
• Penalty of a configuration:
the sum of the penalties of all queens.
• Note: penalty is to be minimized
• Fitness of a configuration:
inverse penalty to be maximized
The 8 queens problem: Mutation
Small variation in one permutation, e.g.:
• swapping values of two randomly chosen positions,
1 3 5 2 6 4 7 8
1 3 7 2 6 4 5 8
The 8 queens problem: Recombination
Combining two permutations into two new permutations:
• choose random crossover point
• copy first parts into children
• create second part by inserting values from other
parent:
• in the order they appear there
• beginning after crossover point
• skipping values already in child
1 3 5 2 6 4 7 8
8 7 6 5 4 3 2 1
1 3 5 4 2 8 7 6
8 7 6 2 4 1 3 5
The 8 queens problem: Selection
Parent selection:
–
Pick 5 parents and take best two to undergo
crossover
Survivor selection (replacement)
–
–
–
–
When inserting a new child into the population,
choose an existing member to replace by:
sorting the whole population by decreasing fitness
enumerating this list from high to low
replacing the first with a fitness lower than the given
child
8 Queens Problem: summary
Note that is is only one possible
set of choices of operators and parameters
EC and Global Optimisation
Global Optimisation: search for finding best solution x*
out of some fixed set S
Deterministic approaches
– e.g. box decomposition (branch and bound etc)
– Guarantee to find x* , but may run in superpolynomial time
Heuristic Approaches (generate and test)
– rules for deciding which x S to generate next
– no guarantees that best solutions found are globally
optimal
Genetic Algorithms
GA Quick Overview
Developed: USA in the 1970’s
Early names: J. Holland, K. DeJong, D. Goldberg
Typically applied to:
–
Attributed features:
–
–
discrete optimization
not too fast
good heuristic for combinatorial problems
Special Features:
–
–
Traditionally emphasizes combining information from good
parents (crossover)
many variants, e.g., reproduction models, operators
Genetic algorithms
Holland’s original GA is now known as the
simple genetic algorithm (SGA)
Other GAs use different:
–
–
–
–
Representations
Mutations
Crossovers
Selection mechanisms
SGA technical summary tableau
Representation
Binary strings
Recombination
N-point or uniform
Mutation
Bitwise bit-flipping with fixed
probability
Parent selection
Fitness-Proportionate
Survivor selection
All children replace parents
Speciality
Emphasis on crossover
Representation
Phenotype space
Encoding
(representation)
Genotype space =
{0,1}L
10010001
10010010
010001001
011101001
Decoding
(inverse representation)
SGA reproduction cycle
1. Select parents for the mating pool
(size of mating pool = population size)
2. Shuffle the mating pool
3. For each consecutive pair apply crossover with
probability pc , otherwise copy parents
4. For each offspring apply mutation (bit-flip with
probability pm independently for each bit)
5. Replace the whole population with the resulting
SGA operators: 1-point crossover
Choose a random point on the two parents
Split parents at this crossover point
Create children by exchanging tails
Pc typically in range (0.6, 0.9)
SGA operators: mutation
Alter each gene independently with a probability pm
pm is called the mutation rate
–
Typically between 1/pop_size and 1/ chromosome_length
SGA operators: Selection
Main idea: better individuals get higher chance
– Chances proportional to fitness
– Implementation: roulette wheel technique
Assign to each individual a part of the
roulette wheel
Spin the wheel n times to select n
individuals
1/6 = 17%
A
3/6 = 50%
B
C
fitness(A) = 3
fitness(B) = 1
2/6 = 33%
fitness(C) = 2
An example
Simple problem: max x2 over {0,1,…,31}
GA approach:
–
–
–
–
–
Representation: binary code, e.g. 01101 13
Population size: 4
1-point xover, bitwise mutation
Roulette wheel selection
Random initialisation
We show one generational cycle done by hand
x2 example: selection
X2 example: crossover
X2 example: mutation
The simple GA
Has been subject of many (early) studies
–
still often used as benchmark for novel GAs
Shows many shortcomings, e.g.
–
–
–
–
Representation is too restrictive
Mutation & crossovers only applicable for bit-string &
integer representations
Selection mechanism sensitive for converging
populations with close fitness values
Generational population model (step 5 in SGA repr.
cycle) can be improved with explicit survivor selection
Alternative Crossover Operators
Performance with 1 Point Crossover depends on the
order that variables occur in the representation
–
more likely to keep together genes that are near
each other
–
Can never keep together genes from opposite ends
of string
–
This is known as Positional Bias
–
Can be exploited if we know about the structure of
our problem, but this is not usually the case
n-point crossover
Choose n random crossover points
Split along those points
Glue parts, alternating between parents
Generalisation of 1 point (still some positional bias)
Two-point Crossover
Two points are chosen in the strings
The material falling between the two points
–
is swapped in the string for the two offspring
Example:
Uniform crossover
Assign 'heads' to one parent, 'tails' to the other
Flip a coin for each gene of the first child
Make an inverse copy of the gene for the second child
Inheritance is independent of position
Cycle crossover example
Step 1: identify cycles
Step 2: copy alternate cycles into offspring
Crossover OR mutation?
Decade long debate: which one is better / necessary /
main-background
Answer (at least, rather wide agreement):
–
–
–
–
it depends on the problem, but
in general, it is good to have both
both have another role
mutation-only-EA is possible, xover-only-EA would not work
Crossover OR mutation? (cont’d)
Exploration: Discovering promising areas in the search
space, i.e. gaining information on the problem
Exploitation: Optimising within a promising area, i.e. using
information
There is co-operation AND competition between them
Crossover is explorative, it makes a big jump to an area
somewhere “in between” two (parent) areas
Mutation is exploitative, it creates random small
diversions, thereby staying near (in the area of ) the parent
Crossover OR mutation? (cont’d)
Only crossover can combine information from two
parents
Only mutation can introduce new information (alleles)
Crossover does not change the allele frequencies of
the population (thought experiment: 50% 0’s on first
bit in the population, ?% after performing n
crossovers)
To hit the optimum you often need a ‘lucky’ mutation
Other representations
Gray coding of integers (still binary chromosomes)
–
Gray coding is a mapping that means that small changes in
the genotype cause small changes in the phenotype (unlike
binary coding). “Smoother” genotype-phenotype mapping
makes life easier for the GA
Nowadays it is generally accepted that it is better to
encode numerical variables directly as
Integers
Floating point variables
Integer representations
Some problems naturally have integer variables, e.g.
image processing parameters
Others take categorical values from a fixed set e.g.
{blue, green, yellow, pink}
N-point / uniform crossover operators work
Extend bit-flipping mutation to make
–
–
“creep” i.e. more likely to move to similar value
Random choice (esp. categorical variables)
Real valued problems
Many problems occur as real valued problems, e.g.
continuous parameter optimisation f : n
Illustration: Ackley’s function (often used in EC)
Floating point mutations
Uniform mutation:
Analogous to bit-flipping (binary) or random resetting
(integers)
xi drawn randomly (uniform) from LBi ,UBi
Floating point mutations
Non-uniform mutations:
–
–
–
–
Many methods proposed,such as time-varying
range of change etc.
Most schemes are probabilistic but usually only
make a small change to value
Most common method is to add random deviate to
each variable separately, taken from N(0, )
Gaussian distribution and then curtail to range
Standard deviation controls amount of change
(2/3 of drawingns will lie in range (- to + )
Simple arithmetic crossover
•
•
•
Parents: x1,…,xn and y1,…,yn
Pick random gene (k) after this point mix values
child1 is:
x , ..., x , y
(1 ) x
, ..., y (1 ) x
1
k
k 1
k 1
n
n
•
reverse for other child. e.g. with = 0.5
Cycle crossover
Basic idea:
Each allele comes from one parent together with its position.
Informal procedure:
1. Make a cycle of alleles from P1 in the following way.
(a) Start with the first allele of P1.
(b) Look at the allele at the same position in P2.
(c) Go to the position with the same allele in P1.
(d) Add this allele to the cycle.
(e) Repeat step b through d until you arrive at the first allele of P1.
2. Put the alleles of the cycle in the first child on the positions
they have in the first parent.
3. Take next cycle from second parent
Cycle crossover example
Step 1: identify cycles
Step 2: copy alternate cycles into offspring
Edge Recombination
Works by constructing a table listing which
edges are present in the two parents, if an
edge is common to both, mark with a +
e.g. [1 2 3 4 5 6 7 8 9] and [9 3 7 8 2 6 5 1 4]
Edge Recombination 2
Informal procedure once edge table is constructed
1. Pick an initial element at random and put it in the offspring
2. Set the variable current element = entry
3. Remove all references to current element from the table
4. Examine list for current element:
–
–
–
If there is a common edge, pick that to be next element
Otherwise pick the entry in the list which itself has the shortest list
Ties are split at random
5. In the case of reaching an empty list:
–
–
Examine the other end of the offspring is for extension
Otherwise a new element is chosen at random
Edge Recombination example
Multiparent recombination
Recall that we are not constricted by the practicalities
of nature
Noting that mutation uses 1 parent, and “traditional”
crossover 2, the extension to a>2 is natural to examine
Been around since 1960s, still rare but studies indicate
useful
Three main types:
–
–
–
Based on allele frequencies, e.g., p-sexual voting generalising
uniform crossover
Based on segmentation and recombination of the parents, e.g.,
diagonal crossover generalising n-point crossover
Based on numerical operations on real-valued alleles, e.g.,
center of mass crossover, generalising arithmetic
recombination operators
Fitness Based Competition
Selection can occur in two places:
–
–
Selection operators work on whole individual
–
Selection from current generation to take part in
mating (parent selection)
Selection from parents + offspring to go into next
generation (survivor selection)
i.e. they are representation-independent
Distinction between selection
–
–
operators: define selection probabilities
algorithms: define how probabilities are implemented
Tournament Selection
All methods above rely on global population
statistics
–
–
Could be a bottleneck esp. on parallel machines
Relies on presence of external fitness function
which might not exist: e.g. evolving game players
Informal Procedure:
–
–
Pick k members at random then select the best of
these
Repeat to select more individuals
Tournament Selection 2
Probability of selecting i will depend on:
–
–
Rank of i
Size of sample k
–
Whether contestants are picked with replacement
–
higher k increases selection pressure
Picking without replacement increases selection pressure
Whether fittest contestant always wins
(deterministic) or this happens with probability p
For k = 2, time for fittest individual to take over
population is the same as linear ranking with s = 2 • p
Survivor Selection
Most of methods above used for parent
selection
Survivor selection can be divided into two
approaches:
–
Age-Based Selection
–
e.g. SGA
In SSGA can implement as “delete-random” (not
recommended) or as first-in-first-out (a.k.a. delete-oldest)
Fitness-Based Selection
Using one of the methods above
Example application of order based GAs: JSSP
Precedence constrained job shop scheduling problem
J is a set of jobs.
O is a set of operations
M is a set of machines
Able O M defines which machines can perform which
operations
Pre O O defines which operation should precede which
Dur : O M IR defines the duration of o O on m M
The goal is now to find a schedule that is:
Complete: all jobs are scheduled
Correct: all conditions defined by Able and Pre are satisfied
Optimal: the total duration of the schedule is minimal
Precedence constrained job shop scheduling GA
Representation: individuals are permutations of operations
Permutations are decoded to schedules by a decoding procedure
–
–
–
take the first (next) operation from the individual
look up its machine (here we assume there is only one)
assign the earliest possible starting time on this machine, subject to
machine occupation
precedence relations holding for this operation in the schedule created so far
fitness of a permutation is the duration of the corresponding
schedule (to be minimized)
use any suitable mutation and crossover
use roulette wheel parent selection on inverse fitness
Generational GA model for survivor selection
use random initialisation
An Example Application to
Transportation System Design
Taken from the ACM Student Magazine
–
Undergraduate project of Ricardo Hoar & Joanne Penner
Vehicles on a road system
–
Modelled as individual agents using ANT technology
Want to increase traffic flow
Uses a GA approach to evolve solutions to:
–
–
(Also an AI technique)
The problem of timing traffic lights
Optimal solutions only known for very simple road systems
Details not given about bit-string representation
–
But traffic light switching times are real-valued numbers over a
continuous space
Transport Evaluation Function
Traffic flow is increased if:
–
–
The average time a car is waiting is decreased
Alternatively, the total waiting time is decreased
They used this evaluation function:
Wi is the total waiting time for car i and di is the
total driving time for car i.