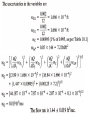Download Lecture Presentation Chp-10

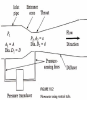
CHAPTER 1O
<The Last Chapter>
Measuring Fluid Flow Rate,
Fluid Velocity,
• Bernoulli equation takes the form of
where V is the fluid velocity, P is the fluid pressure, z is the
elevation of the location in the pipe relative to a specified
reference elevation (datum), ρ is the fluid density, and g is
gravity
The velocities at two axial locations in the duct with
different areas are related through the conservation
of mass equation,
where, A is the duct crosssectional area and
is the fluid mass flow rate
(e.g., kg/s).
For an incompressible fluid,
the density is constant.
is usually written in the form:
Equations can be combined to obtain an expression
The theoretical basis for a class of flow meters in which
the flow rate is determined from the pressure change
caused by variation in the area of a conduit.
is used to account for nonideal effects.
and a parameter called the Reynolds number,
which is defined as
When z1 = z2 Flow Rate Equation becomes as follows:
The Reynolds number is a dimensionless parameter,
The venturi , thus operating within the range of data in Table 10.1.
Coriolis Mass Flowmeter The Coriolis force is a force that occurs when dynamic problems are
analyzed within a rotating reference frame. Useful flowmeters based on this effect are now
widely used in the process industries. Consider a fluid flowing through the U-shaped tube shown
in Figure 10.13(a).The tube is cantilevered out from a rigidly supported base. An
electromechanical driver is used to vibrate the free end of the tube at its natural frequency in the
y direction. The amplitude of this vibration will be largest at the end of the cantilever and zero at
the base. Consider an instant in time when the tube is moving in the -y direction. The fluid
moving through the tube away from the base will not only have a component of velocity in the x
direction but also in the -y direction, and the magnitude of this y component will increase with
distance from the base. As a fluid particle moves along the tube, it is thus accelerating in the -y
direction. This acceleration is caused by a Coriolis force in the -y direction applied by the tube
wall. The resultant reaction on the tube wall is a force, F in the *y direction. For the fluid
returning to the base, the y component of fluid velocity is decreasing in the flow direction. This
results in a Coriolis force on the tube wall in the -y direction.