* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Flip-flop (electronics) wikipedia , lookup
Power inverter wikipedia , lookup
History of electric power transmission wikipedia , lookup
Signal-flow graph wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Public address system wikipedia , lookup
Flexible electronics wikipedia , lookup
Ground (electricity) wikipedia , lookup
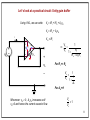
Electrical substation wikipedia , lookup
Audio power wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Alternating current wikipedia , lookup
Current source wikipedia , lookup
Stray voltage wikipedia , lookup
Voltage optimisation wikipedia , lookup
Surge protector wikipedia , lookup
Buck converter wikipedia , lookup
Voltage regulator wikipedia , lookup
Integrated circuit wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Negative feedback wikipedia , lookup
Mains electricity wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Two-port network wikipedia , lookup
Regenerative circuit wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
TECHNIQUES OF DC CIRCUIT ANALYSIS: Application to operational amplifier circuit SKEE 1023 1 Operational amplifier: Integrated circuit consisting several transistors and resistors normally used for analog circuit design. Offset null(5) Inverting input (2) Non-inverting input (3) − Positive supply Vcc+ (7) Output (6) + Offset null(1) Negative supply Vcc− (4) 2 Operational amplifier: Integrated circuit consisting several transistors and resistors normally used for analog circuit design. How can we analyse circuit containing op-amps (consistings of hundreds of transistors and resistors!) using the knowledge that we have so far? The answer is modeling ! An op-amp can be modeled by a very good voltage amplifier circuit Later we’ll see that the analysis is even simplified when we assumed an ideal op-amp. 3 vo = Avd = A(v2 - v1) vo - output voltage with respect to ground v1 A - − vd + v2 Ro Ri + − Avd v0 open loop gain v1 - inverting input voltage with respect to ground v2 - non-inverting input voltage with respect to ground An op-amp can be modeled by a very good voltage amplifier circuit 4 An op-amp can be modeled by a very good voltage amplifier circuit vo = Avd = A(v2 - v1) vo - output voltage with respect to ground v1 A - − vd + v2 Ro Ri + − open loop gain v1 - inverting input voltage with respect to ground v0 v2 - non-inverting input voltage with respect to ground Avd vo Positive saturation Vcc -Vcc/A Vcc/A vd Negative saturation -Vcc 5 Let’s look at a practical circuit: Unity gain buffer + − Vcc + Vs + − − + • In drawing op-amp circuits, we normally do not include power supplies vo − + Vcc − 6 Let’s look at a practical circuit: Unity gain buffer + Vs + − − + • In drawing op-amp circuits, we normally do not include power supplies vo − 7 Let’s look at a practical circuit: Unity gain buffer Using KVL, we can write: Vs = iRi + iRo + Aovin Vo = iRo + Aovin i Vin = iRi + Vs + − + Ro R vin i − + − Aovin − Vo Vs 1 + vo 1 Ri Ro Ao Ri For Ri >> Ro Vo 1 Vs 1 1 Ao − For Ao>>1 Whenever vin 0 , Aovin increases until vin=0 and hence the current cease to flow. Vo 1 Vs 8 Modeling of an ideal op-amp 1. In previous analysis we have assumed Ri>>Ro In practical op-amps it is true that Ri >> Ro and for ideal op-amp we will assume Ri → and Ro → 0 2. In previous analysis we have assumed Ao>> 1 In practical op-amps it is true that Ao>> 1 and for ideal op-amp we will assume Ao → As a result of 1 and 2, when analysing an op-amp circuit with feedback, we will assume that: i. i1 = 0, and i2 = 0 ii. v2 –v1 = 0 9 Let’s look back at the buffer circuit using ideal op-amp Since vo is tied to v1 and in ideal op-amp v1=v2, it is obvious that vo = Vs (as we have seen before) v2 + Vs + − v1 − + vo − 10 Eg.2 (PP 5.2) Find the closed-loop gain vo/vs. Determine current i when vs = 2V 11 OP AMP circuits In SKEE1023, we will study some of the important op amp circuits: • • • • Inverting amplifier Non-inverting amplifier Summing amplifier Difference amplifier You should : • Know how (not memorize!) to derive the input-output relationship (Gain = vo/vi)) • Able to identify the circuit correctly 12 Inverting Amplifier Reverses the polarity of a signal while amplifying it Since i1 = i2, and v1 = v2 = 0 Rf vi 0 0 vo vo vi R1 Rf Ri 13 Non-inverting Amplifier Maintains the polarity of a signal while amplifying it Since i1 = i2, and v1 = v2 = vi vi vi vo R1 Rf 1 1 1 vi vo Rf Rf R1 Rf vi vo 1 R1 14 Summing Amplifier Output is the inverted, scaled sum of the voltages applied to the input KCL at node a gives: i = i1 + i2 + i3 And, since v+ = v- = 0 v o v1 v 2 v 3 Rf R1 R2 R3 R R R v o f v 1 f v 2 f v 3 R2 R3 R1 15 Difference Amplifier Output is proportional to the difference between the two inputs voltages Using voltage division rule, R4 v 2 v b R4 R3 With va = vb, applying KCL at the inverting input, v1 v b v b v o R1 R2 16 Difference Amplifier Output is proportional to the difference between the two inputs voltages It can be shown that: If R1 R3 R2 R 4 R2 1 R1 R2 R2 vo v 2 v1 R R1 R1 1 3 R4 vo R2 v 2 v1 R1 17