* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Superposition and
Power electronics wikipedia , lookup
Integrating ADC wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Index of electronics articles wikipedia , lookup
Surge protector wikipedia , lookup
Radio transmitter design wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Current source wikipedia , lookup
Flexible electronics wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Negative-feedback amplifier wikipedia , lookup
Integrated circuit wikipedia , lookup
Regenerative circuit wikipedia , lookup
Two-port network wikipedia , lookup
Current mirror wikipedia , lookup
Rectiverter wikipedia , lookup
RLC circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Opto-isolator wikipedia , lookup
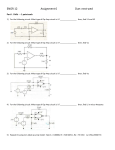
5/14/2017 582770715 1/4 Superposition and Op-Amp Circuits Consider this op-amp circuit, with two input voltages (v1 and v2): R2 R1 v1 - v2 ideal R3 vout + R4 The easiest way to analyze this circuit is to apply superposition! Recall that op-amp circuits are linear, so superposition applies. Our first step is to set all sources to zero, except v2 —in other words, set v1 =0 (connect it to ground potential): 5/14/2017 582770715 2/4 R2 R1 - v2 ideal R3 v vo2 + i 0 R4 Since the current into the non-inverting input of the op-amp is zero (i 0 ), it is evident that: v R4 v R3 R4 2 Likewise, the remainder of the circuit is simply the noninverting amplifier, where: R vo 2 1 2 v R1 Combining these two equations, we get: 5/14/2017 582770715 3/4 R R4 vo 2 1 2 v2 R R R 1 3 4 Now for the second step. Turn off all sources except v1 —in other words set v2 =0: R2 R1 v1 i 0 v ideal R3 v vo1 + i 0 R4 It is evident that the since the current into the non-inverting terminal of the op-amp is zero, the voltage v+ is likewise zero. Thus, the circuit above is simply an inverting amplifier, where: vo 1 R2 v R1 1 5/14/2017 582770715 4/4 There are no more sources in this circuit, so that we can conclude from superposition that the output voltage is the sum of our two, single-source solutions: vout vo 1 vo 2 R2 R R4 1 2 v 2 v1 R1 R3 R4 R1 Note this circuit is effectively a weighted difference amplifier.