Download Ch 5 Homework Name: edition. Follow the instructions and show your

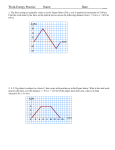
Ch 5 Homework
Name:
Homework problems are from the Serway & Vuille 10th edition. Follow the instructions and show your
work clearly.
1. (Problem 4)
A shopper in a supermarket pushes a cart with a force of 35 N directed at an angle of 25° below the
horizontal. The force is just sufficient to overcome various frictional forces, so the cart moves at
constant speed.
(a) Draw a diagram of the shopper and the cart.
(b) Find the work done by the shopper as she moves down a 50.0-m length aisle.
(c) What is the net work done on the cart? Explain your answer.
(d) The shopper goes down the next aisle, pushing horizontally and maintaining the same speed as
before. If the work done by frictional force doesn’t change, would the shopper’s applied force
be larger, smaller, or the same? What about the work done on the cart by the shopper?
2.(Problem 5)
Starting from rest, a 5.00-kg block slides 2.50 m down a rough 30.0° incline. The coefficient of kinetic
friction between the block and the incline is μk = 0.436.
(a) Draw a diagram of the block on the incline.
(b) Draw a free-body diagram of the 5.00-kg block.
(c) Determine the work done by the force of gravity.
(d) Determine the work done by the friction force between block and incline.
(e) Determine the work done by the normal force.
(f) Qualitatively, how would the answer change if a shorter ramp at a steeper angle were used to
span the same vertical height?
3. (Problem 13)
A 70-kg base runner begins his slide into second base when he is moving at a speed of 4.0 m/s. The
coefficient of friction between his clothes and Earth is 0.70. He slides so that his speed is zero just as he
reaches the base.
(a) Draw a diagram of the runner and label all physical quantities in this problem.
(b) How much mechanical energy is lost due to friction acting on the runner?
(c) How far does he slide?
4. (Problem 25)
A daredevil on a motorcycle leaves the end of a ramp with a speed of 35.0 m/s as in figure below. If his
speed is 33.0 m/s when he reaches the peak of the path, what is the maximum height that he reaches?
Ignore friction and air resistance.
(a) Define coordinate system on the figure above.
(b) Calculate his/her initial kinetic and potential energy and find the sum of the kinetic and the
potential energy.
(c) Calculate the sum of kinetic and potential energy at the maximum height in terms of h.
(d) Calculated h.
5. (Problem 30)
A projectile of mass m is fired horizontally with an initial speed of v0 from a height of h above a flat,
desert surface. Neglecting air friction, at the instance before the projectile hits the ground, find the
following in terms of m, v0, h, and g.
(a) Draw a diagram of the projectile and define a coordinate system.
(b) Find the work done by the force of gravity on the projectile.
(c) Find the change in kinetic energy of the projectile since it was fired.
(d) Find the final kinetic energy of the projectile.
(e) Calculate the final speed of the projectile from the answer in the part (d)
(f) Remember you can also find the final speed by using the equations in the chapter 3. Calculate
the final speed(magnitude of the final velocity) by using the equations for a motion under a
constant acceleration, and compare your result with the answer in the part (e).(Hint: review one
of your homework problem.)
(g) Are any of the answers changed if the initial angle is changed?
6. (Problem 31)
A horizontal spring attached to a wall has a force constant of 850 N/m. A block of mass 1.00 kg is
attached to the spring and oscillates freely on a horizontal, frictionless surface as in the figure below.
The initial goal of this problem is to find the velocity at the equilibrium point after the block is released.
(a) What objects constitute the system, and through what forces do they interact?
(b) Define coordinate systems on the figure above (define x=0 point at the equilibrium) and label all
the physical quantities, using letters (i.e. Mass of block = m).
(c) Find the energy stored in the spring when the mass is stretched 6.00 cm from equilibrium and
again when the mass passes through equilibrium after being released from rest.
(d) Write the conservation of energy equation for this situation and solve it for the speed of the
mass as it passes equilibrium. Use variables you define in this part.
(e) Substitute numbers to obtain a numerical value.
(f) What is the speed at the half way point?(x = 3.00 cm) Why isn’t it half the speed at the
equilibrium?
7. (Problem 38)
Two blocks are connected by a light string that passes over a frictionless pulley as in Figure below. The
system is released from rest while m2 is on the floor and m1 is a distance h above the floor.
(a) Define a coordinate system on the figure above.
(b) Assuming m1 > m2 find an expression for the speed of m1 just as it reaches the floor.
(c) Taking m1 = 6.5 kg, m2 =4.2 kg and h = 3.2 m, evaluate your answer to part (b).
(d) Find the speed of the block when m1 has fallen a distance of 1.6 m.
(e) This problem can be solved by using force analysis as well. Draw a free-body diagram of the m1
and m2 separately.
(f) Write down the forces when the m1 and m2 just start to move. (m2 is not on the floor at this
point).
m1
Force variable
Net Force(Fnet 1)
m2
value(N)
Force variable
value(N)
Net Force(Fnet 2)
(g) Find the acceleration of the block m1 and m2 from the equations you find in the part (f).
(h) Find the speed of the m1 just as it reaches the floor from the acceleration you find in the part (g)
and compare your result with the answer in the part (b)
8. (Problem 57)
A
-kg car starts from rest and accelerates uniformly to 18.0 m/s in 12.0 s. Assume that air
resistance remains constant at 400 N during this time.
(a) Draw a diagram of the car and label all the physical quantities in the diagram, using letters you
choose.
(b) Find the average power developed by the engine.
(c) Find the instantaneous power output of the engine at t = 12.0s, just before the car stops
accelerating.
9. (Problem 64)
A boy starts at rest and slides down a frictionless slide as in Figure below. The bottom of the track is a
height h above the ground. The boy then leaves the track horizontally, striking the ground a distance d
as shown. Using energy methods, determine the initial height H of the boy in terms of h and d.
(a) Define a coordinate system on the diagram above.
(b) Find the horizontal velocity of the boy when he is a height h above the ground in terms of H, h,
and g.
(c) Determine the distance d, by using the equations you learned in chapter 3, and write d in terms
of H and h.
(d) Solve the answer in the part (c) for H and determine the H in terms of h and d.
10. (Problem 92) Two blocks, A and B (with mass 50 kg and 100 kg, respectively), are connected by a
string, as shown in Figure below. The pulley is frictionless and of negligible mass. The coefficient of
kinetic friction between block A and the incline is μk =0.25. Determine the change in the kinetic energy
of block A as it moves from Ⓒ toⒹ, a distance of 20 m up the incline (and block B drops downward a
distance of 20 m) if the system starts from rest.
(a) Define a coordinate system on the diagram above and label all the physical quantities, by using
variables you choose.
(b) Draw free-body diagrams of block A and B separately and define a coordinate system for each
block.
(c) Write down forces acting on the block A.
Force variable
Net Force(Fnet x)
x-direction
value(N)
Force variable
y-direction
value(N)
Net Force(Fnet y)
(d) From part (c), find the friction between the block A and the incline.(using variables in this part)
(e) Determine the change in the kinetic energy of block A as it moves from Ⓒ toⒹ by using energy
methods.
(f) Calculate the final velocity of the block A from part (e)
(g) Find the final velocity by using force analysis and the equations of motion under a constant
acceleration.