* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Transmission (mechanics) wikipedia , lookup
Mitsubishi AWC wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Virtual work wikipedia , lookup
Old quantum theory wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Sagnac effect wikipedia , lookup
Fictitious force wikipedia , lookup
Center of mass wikipedia , lookup
Coriolis force wikipedia , lookup
Hunting oscillation wikipedia , lookup
Quaternions and spatial rotation wikipedia , lookup
Tensor operator wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Earth's rotation wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
Accretion disk wikipedia , lookup
Jerk (physics) wikipedia , lookup
Moment of inertia wikipedia , lookup
Photon polarization wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Angular momentum wikipedia , lookup
Angular momentum operator wikipedia , lookup
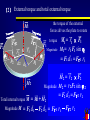
Chapter 4 Rotation of rigid body §4.1 The rotation of a rigid body about a fixed axis §4.2 Torque , the law of rotation , moment of inertia §4.3 Angular momentum the law of angular momentum conservation §4.4 work done by a torque, the theorem of kinetic energy of a rigid body rotating about a fixed axis Summary §4.1 The rotation of a rigid body about a fixed axis 1. the angular velocity and angular acceleration of a rotating rigid body 2. Formulation of fixed axis rotation with constant angular acceleration 3. The relationship between angular quantities and linear quantities Rigid body:under external forces if the shape and size of an object do not change .(the distance between any two arbitrary points in the object is a constant) explain:⑴ Rigid body is an idealized object ⑵ The model of the rigid body is introduced for trying to simplify the study of the motion. The motion of a rigid body:the translation rotation. 1 the angular velocity and angular acceleration of a rotating rigid body 1. Angular coordinate Rigid body Equation motion of rotating rigid body about a fixed axis Rotation clockwise rotation counter clockwise An arbitray point in (t+△t) (t) Reference q>0 q<0 direction Reference plane which is perpendicular to the Oz 2. Angular displacement axis) Axis q q (t t ) q (t ) 3. Angular velocity q dq direction of : determined by right lim t 0 hand rule t dt 1 the angular velocity and angular acceleration of a rotating rigid body The rotation direction can be expressed by the positive or negative of the angular velocity, when the rigid body rotating about a fixed z z axis <0 >0 (i) When rotating counter clockwise, > 0; (ii) When rotating clockwise, < 0; 4. angular acceleration When > 0 d dt (i) When >0, the rigid body rotates with acceleration;. (ii) When <0, the rigid body rotates with deceleration. The Features of Rotation about a Fixed Axis: (1) The location and direction of rotation axis are fixed relative to a inertial reference frame. ( 2 ) Every point of body moves in a circle whose center lies on rotation axis and radius different. (3) Every point moves through the same angle during a particular time interval;q , , (4) Each rotation planeis perpendicular to rotation axis.. 2 Formula of fixed axis rotation with constant angular acceleration A rotation with variable angular velocity is called fixed axis rotation with constant angular acceleration . Straight line motion with constant linear acceleration Fixed axis rotation constant angular acceleration 0 t v v 0 at 2 2 1 1 x x0 v0t 2 at q q 0 0t 2 t 2 2 2 2 v v 0 2a( x x0 ) 0 2 (q q 0 ) 3 The relationship between angular quantities and linear quantities dq ω dt 2 dω d q 2 dt dt v rωet a t r an rω 2 an a r P at 2 a ret rω en et v Example 1 In a mini-motor rotates in a high speed, in which a cylindrical rotor rotates about an axis that is perpendicular to the cross-section and passed through is center. Initially, the angular speed of the mini-motor is zero then it up in a time relationship of m (1 e t / ) , where m 540 r s 1,. 2.0 s (1) what is the rotate speed of the mini-motor at t =6 s . (2)how many turns it has made in the time interval of at t =6 s .(3)what is the discipline of the angular acceleration varying with respect of time. Solution: (1) substitute t=6 s to ω m (1 e t / ) ω 0.95ωm 513 r s 1 (2) The turns the motor has made in the time interval of t=6 s is 1 6 1 6 t / N ω d t ω ( 1 e )dt m 2π 0 2π 0 2.2110 r 3 (3) The angular acceleration of the motor is d m t / t / 2 2 e 540 πe rad s dt Example 2 An electric motor rotates with a high speed, in which a cylindrical rotor can rotate about the axis going through its center and perpendicular to the cross – section area of the rotator. Initially, the angular velocity is ω0 0 . After 300 s the speed reached 18000 r/min. it is known that the angular acceleration a of the rotation is proportional to time. How many revolutions has the turned in this time interval? d Solution : ct , ct , d t integrating both side t 0 d c0 tdt 1 2 得 ct 2 1 2 ct 2 at t =300 s 18 000 r min 1 600π rad s 2 2 600 π π 3 c 2 rad s 2 t 300 75 1 2 π 2 ct t 2 150 1 dq π 2 from t dt 150 q π t 2 We have dq t dt 0 150 0 π 3 q t rad 450 The rotator has made the following revolutions in 300 s q π N 2π (300) 3 10 3 2π 450 4 §4.2 Torque, the law of rotation, moment of inertia 1. 2. 3. 4. Torque The law of rotation The power of torque The theorem of parallel axes 1 Torque Describe the effect of force on the rotation of a rigid body. d r sin q the torque of force F Right hand rule Is the arm of force with respect to axis z is M M Fr sin q Fd M r F F z O r Fi 0, F Mi 0 F d Fi 0, i q P When the combined force is zero, their combined torque may not be zero F * F Mi 0 i discussion F is not in the rotation plane , (1)If the force it can be decomposed into two components with parallel and normal to the rotation axis. F Fz F where the torque of Fz is zero, so the torque of F is M z k r F M z rF sin q z k O F Fz r q F (2) External torque and total external torque the torque of the external forces drives the plate to rotate M1 F2 F 1 F 2 j2 r2 P2 O r1 d2 d1 P1 F1 j1 torque Magnitude 方向 M2 Magnitude M1 = r1 × F1 M1 = r1 F1 sin j1 = F1 d 1 = F 1 r1 M M 2 = r 2 × F2 M 2 = r 2F 2 sin F j2 = F2 d 2 = F 2 r2 = M1 + M 2 r Magnitude M = F1 d 1 F2 d 2 = F 1 r1 叉乘右螺旋 F 2 r2 Total internal torque M The total external torque is equal to the algebraic sum of these external torque M M1 M 2 M 3 (3)The combined torque generated by the internal forces between the mass points in a rigid body is 0, i.e. M ij M内 M ij 0 j rj i, j F ji O r i F ij z d i M ji F M ij M ji (4) The torque is zero, when the force acting on the axis O M 0 2 M ( m r ej j j )α j z Moment of inertia J m r 2 j j j J r dm 2 O r j Fej m j Fij The law of rotation M J when the rigid body rotates about a fixed axis, the angular acceleration is proportional to the combined external torque that the rigid body is subject to, and it is inversely proportional to the moment of inertia of the rigid body. The law of rotation M J discussion M 0, ω M (2) J (1) (3) is a constant d M J J dt Exercises p.144 / 4- 6, 7, 9 §4.3 Angular momentum, the law of angular momentum conservation 1. The theorem of angular momentum and the law of the conservation of the angular momentum of mass points 2. The theorem of angular monentum and the priciple of conservation of angular momentum of a rigid body rotating §4.3 Angular momentum, the law of angular momentum conservation The accumulation effect of forces over time: Impulse 、Momentum、 the theorem of momentum. The accumulation effect of Torque over time: Impulse torque、 Angular momentum 、 the theorem of angular momentum of a rigid body rotating about a fixed axis. 1 The theorem of angular momentum and the law of the conservation of the angular momentum of mass points 2 p mv,Ek mv 2 Description for the motion of a mass point Can we use the momentum to descript the motion of a rigid body ? 0, p 0 0, p 0 pi pj “momentum ” is not good physical q the rotation of the rigid body . to describe to 1 mM m 1 mM m 2 2 mv A G mvB G 2 Rh 2 R mM mM v v 2G 2G Rh R 2 A 2 B v A 1 615 m s so 1 v ( v v ) and (m)u 2 A 2 12 0 100 m s 1 mv m mv u 120 kg Exercises p.144 / 4- 13, 19, 28 §4.4 Work Done by a Torque 1. Work done by a torque 2. The power of a torque 3. The kinetic energy of rotation 4. The theorem of kinetic energy of a rigid body rotating about a fixed axis The accumulation effect of forces over space: Work 、Kinetic energy、 the theorem of Kinetic energy . The accumulation effect of Torque over space: Work done by a torque、the kinetic energy of rotation、 the theorem of Kinetic energy of a rigid body rotating about a fixed axis. 1 Work done by a Torque dW F dr Ft ds Ft rdq dW Mdq Work done by a torque: 2 q2 W Mdq The power of a torque q1 dW dq P M M dt dt Comparing to W F dr P F v 3 The kinetic energy of rotation For a mass element the line sped is The kinetic energy of the mass element is The kinetic energy of the entire rigid body is ∑ ∑ Moment of inertia J We have J 4 The theorem of kinetic energy of a rigid body rotating about a fixed axis The theorem of Kinetic energy of a mass point: The theorem of Kinetic energy of a rigid body rotating: From the element of work done by the external torque The law of rotation so The work done by the combined external torque The increment of the rotation kinetic energy of the rigid body Example 1 The turnplate of a gramophone rotates in an angular velocity ω about the axis which goes through the center of the plate. After a record being put on it, the record will rotate will rotate with the turnplate under the action of friction force. Assume the radius of the plate is R and the mass is m,the friction factor is .(1)what is the magnitude of the torque of the friction force; (2)how long does the record need when its angular velocity reachesω ;(3)what is the work done by the drive force of the turn plate in this period of time ? Solution (1) as shown in df figure, an element area, ds = drdl, the friction force of which the element subjected is df mg πR 2 o drdl R The torque of the friction force to the point O on the rotating axis of the trunplate is rdf mg πR 2 rdrdl r dl dr df for the cirque with a width dr, the torque of friction force that the turnplate subject is mg dM rdr (2πr ) 2 πR o R 2mg 2 r dr 2 R 2mg R 2 2 M r dr Rmg 2 0 R 3 r dl dr is (the (2) According to the theorem of angular momentum moment of inertia of record is J=mR2/2) M 4g J 3R Based on 0 t 3R t 4g ( the record makes a rotation motion with a uniform acceleration ) (3) From 2 2 2q 0 the time interval of 0 to t is the angle that the record turns in The word done by the drive force of the turnplate in this time interval is 1 2 2 W Mq mR 4 3 2 R q 8g Example 2 A rod of length is l and mass m’ can rotate about pivot O freely, a bullet with mass m and speed v is shot into the point with distance a away from the pivot, rendering a 30o . Deflection angle of the rod with respect to the vertical axis, what is the initial speed of the? Solution o a v m 30 ' Take the bullet and the rod as a system, the angular momentum of the system should be conserved 1 2 3 m v a 2 mva ( ml ma ) 3 m'l 2 3ma 2 After the bullet gets into the rod, taking the bullet, the rod and the earth as a system, the mechanical momentum of the system should be conserved ,E =constant. 1 1 2 2 2 ( m l ma ) 2 3 o a v m 30 ' l o mga(1 cos 30 ) m g (1 cos 30 ) 2 o 2 2 v g (2 3 )(m l 2ma)(m l 3ma ) 6 ma Exercises p.147 / 4- 30, 31, 36 The end