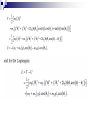Download Lagrange`s equations of motion in generalized coordinates

Phy 303:
Classical Mechanics (2)
Chapter 3
Lagrangian and Hamiltonian Mechanics
Introduction
In solving a problem in dynamics by using the Newtonian
formalism, we must know all the forces acting on the studied
object, because the quantity F that appears in the fundamental
equation F = dP/dt is the total force acting on the object.
But in particular situations, it may be difficult or even impossible
to obtain explicit expressions for all the forces acting on the
object.
An alternate method of dealing with complicated problems in a
general manner is contained in Hamilton's Principle, and the
equations of motion resulting from the application of this
principle are called Lagrange's equations.
Hamiltonian principle
In two papers published in 1834 and 1835, Hamilton announced the
dynamical principle on which it is possible to base all of
mechanics and, indeed, most of classical physics. Hamilton's
Principle may be stated as follows:
Of all the possible paths along which a dynamical system may move from
one point to another within a specified time interval (consistent with any
constraints), the actual path followed is that which minimizes the time
integral of the difference between the kinetic and potential energies.
This principle is also called Principle Of Least Action.
In terms of the calculus of variations, Hamilton's Principle becomes
[1]
If we define the difference of these quantities to be
[2]
then Equation [1] becomes
[3]
The function L appearing in this expression may be identified with the
function f of the variational integral (see Chapter 2),
if we make the transformations
The Euler-Lagrange equations corresponding to Equation [3] are
therefore
[4]
These are the Lagrange equations of motion for the particle, and
the quantity L is called the Lagrange function or Lagrangian for
the particle.
Example 1:
Lagrange equation of motion for the one-dimensional harmonic oscillator.
Substituting these results into Equation [4] leads to
which is identical with the equation of motion obtained using
Newtonian mechanics.
Example 2: Plane pendulum
And applying Lagrange equation:
which again is identical with the Newtonian result
William Rowan Hamilton
Born
4 August 1805)
Dublin
Died
2 September 1865) (aged 60)
Dublin
Fields
Physicist, astronomer, and
mathematician
Joseph Louis Lagrange
Born
25 January 1736)
Turin, Piedmont-Sardinia
Died
10 April 1813) (aged 77)
Paris, FranceFrance
Fields
Mathematics
Mathematical physics
Generalized coordinates
We consider a general mechanical system consisting of a collection
of n discrete point particles, some of which may be connected to
form rigid bodies.
3n quantities must be specified to describe the positions of all the
particles.
If there are m equations of constraint, then only 3n — m coordinates
are independent, and the system is said to possess S = 3n — m
degrees of freedom.
We give the name generalized coordinates to any set of S
independent quantities that completely specifies the state of a
system (their number equals the number of degrees of freedom).
The generalized coordinates are noted q1, q2, . . . , or simply as the qj.
A set of independent generalized coordinates
In certain cases, we use generalized coordinates which number
exceeds the number of degrees of freedom and we explicitly take
into account the constraint relations through the use of the
Lagrange undetermined multipliers.
Such would be the case, for example, if we desired to calculate the
forces of constraint.
The choice of a set of generalized coordinates to describe a system is
not unique. We choose the set that gives the simplest equations
of motion.
, the time derivatives of qj, are called the generalized velocities.
Important Notes on Notation
Cartesian coordinates are noted
Generalized coordinates are noted
(designates the particle)
q j , j  1, 2,...s , s  number of degres of freedom
The index i is reserved for Cartesian coordinates. xi , for i =
1,2,3 , represents either x, y, or z depending on the value of i .
The index α will be used to identify quantities associated with a
given particle when using Cartesian coordinates. For example, the
position vector for particle α is given by rα, and its kinetic energy Tα
Einstein’s summation convention:
Whenever an index appears twice (an only twice), then a summation
over this index is implied. For example,
Lagrange’s equations of motion
in generalized coordinates
In general, the relationships linking the Cartesian and generalized
coordinates and velocities can be expressed as
We may also write the inverse transformations as
Also, there are m equations of constraint of the form
It follows naturally that Hamilton’s Principle can now be expressed in
term of the generalized coordinates and velocities as
[5]
with Lagrange’s equations given by
[6]
if we refer to the definitions of the
quantities in chapter 2 and make the
identifications:
Study Examples 7.1 and 7.3 from the textbook.
Eg 7.3: see textbook
Other example: The double
pendulum.
Consider the case of two particles
of mass m1 and m2 each attached
at the end of a mass less rod of
length l1 and l2 , respectively.
The second rod is also attached to
the first particle (see Figure ).
Derive the equations of motion for
the two particles.
Solution:
It is desirable to use cylindrical coordinates for this problem. We
have two degrees of freedom, and we will choose θ1 and θ2 as the
generalized coordinates.
Starting with Cartesian coordinates, we write an expression for the kinetic
and potential energies for the system (take U=0 at y=0).
And from Lagrange’s equations we get
or
Lagrange’s equations with
undetermined multipliers
If the constraint relations for a problem are given in differential form, we
can incorporate them directly into Lagrange's equations by using the
Lagrange undetermined multipliers (see Chapter 2)
That is, for constraints expressible as
[7]
the Lagrange equations (see chap 2) are
[8]
 The undetermined multipliers
constraint.
k (t ) are closely related to the forces of
The generalized forces of constraint Qj are given by
[9]
Study Example 7.9 from the textbook.
(see textbook)
Equivalence of Lagrange’s and
Newton’s equations
We now explicitly demonstrate the equivalence of Lagrange’s and Newton’s
equations.
Let us choose the generalized coordinates to be the rectangular coordinates.
Lagrange's equations (for a single particle) then become

We also have: for a conservative system:
[10]
and
so Lagrange’s Equations yield the Newtonian equations, as required:
A theorem concerning the kinetic
energy
In a Cartesian coordinates system the kinetic energy of a system of
particles is expressed as
where a summation over i is implied.
Using equations relating the two systems of coordinates:
An important case occurs when a system is scleronomic, i.e., there is
no explicit dependency on time in the coordinate transformation, we
then have
and the kinetic energy can be written in the form
[11]
where a summation on i is still implied
We see that the kinetic energy is also a quadratic function of the
(generalized) velocities.

If we next differentiate equation [11] with respect to ql and then multiply
it by  (and summing), we get
ql
[12]
Conservation theorems
Consider a general Lagrangian L; the total time derivative of L is
(there is summation on j)
But from Lagrange’s equations,
[13]
where we have introduced a new function H called the Hamiltonian of
the system
[14]
 In cases where the Lagrangian is not explicitly dependent on
time we find that
dH
0  H
 cste.
[15]
dt
If we are in presence of a scleronomic system, then
Equation [15] can be written as
(from [12])
 The Hamiltonian of the system is equaled to the total energy
only if the following conditions are met:
1. The system is scleronomic; ie the equations of the transformation
connecting the Cartesian and generalized coordinates must be
independent of time (the kinetic energy is then a quadratic function of
the generalized velocities).
2. The potential energy must be velocity independent.
 The Hamiltonian of the system is conserved (but not necessarily
equal to the total energy) when the Lagrangian is not explicitly
dependent on time.
Canonical equations of motion –
Hamiltonian mechanics.
if the potential energy of a system is velocity independent, then the
linear momentum components in rectangular coordinates are given by
By analogy, in the case in which the Lagrangian is expressed in
generalized coordinates, we define the generalized momenta as
[16]
The Lagrange equations of motion are then expressed by
[17]
Using the definition [16] of the generalized momenta, Equation [14] for
the Hamiltonian may be written as
From [16], the generalized velocities can be expressed as
Thus we may make a change of variables from the
set to the
set and express the Hamiltonian as
[18]