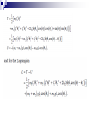* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lagrange`s equations of motion in generalized coordinates
N-body problem wikipedia , lookup
Canonical quantization wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Dynamic substructuring wikipedia , lookup
Hunting oscillation wikipedia , lookup
Centripetal force wikipedia , lookup
Nuclear structure wikipedia , lookup
Path integral formulation wikipedia , lookup
Four-vector wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Classical mechanics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Virtual work wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
First class constraint wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Joseph-Louis Lagrange wikipedia , lookup
Dirac bracket wikipedia , lookup
Equations of motion wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Phy 303: Classical Mechanics (2) Chapter 3 Lagrangian and Hamiltonian Mechanics Introduction In solving a problem in dynamics by using the Newtonian formalism, we must know all the forces acting on the studied object, because the quantity F that appears in the fundamental equation F = dP/dt is the total force acting on the object. But in particular situations, it may be difficult or even impossible to obtain explicit expressions for all the forces acting on the object. An alternate method of dealing with complicated problems in a general manner is contained in Hamilton's Principle, and the equations of motion resulting from the application of this principle are called Lagrange's equations. Hamiltonian principle In two papers published in 1834 and 1835, Hamilton announced the dynamical principle on which it is possible to base all of mechanics and, indeed, most of classical physics. Hamilton's Principle may be stated as follows: Of all the possible paths along which a dynamical system may move from one point to another within a specified time interval (consistent with any constraints), the actual path followed is that which minimizes the time integral of the difference between the kinetic and potential energies. This principle is also called Principle Of Least Action. In terms of the calculus of variations, Hamilton's Principle becomes [1] If we define the difference of these quantities to be [2] then Equation [1] becomes [3] The function L appearing in this expression may be identified with the function f of the variational integral (see Chapter 2), if we make the transformations The Euler-Lagrange equations corresponding to Equation [3] are therefore [4] These are the Lagrange equations of motion for the particle, and the quantity L is called the Lagrange function or Lagrangian for the particle. Example 1: Lagrange equation of motion for the one-dimensional harmonic oscillator. Substituting these results into Equation [4] leads to which is identical with the equation of motion obtained using Newtonian mechanics. Example 2: Plane pendulum And applying Lagrange equation: which again is identical with the Newtonian result William Rowan Hamilton Born 4 August 1805) Dublin Died 2 September 1865) (aged 60) Dublin Fields Physicist, astronomer, and mathematician Joseph Louis Lagrange Born 25 January 1736) Turin, Piedmont-Sardinia Died 10 April 1813) (aged 77) Paris, FranceFrance Fields Mathematics Mathematical physics Generalized coordinates We consider a general mechanical system consisting of a collection of n discrete point particles, some of which may be connected to form rigid bodies. 3n quantities must be specified to describe the positions of all the particles. If there are m equations of constraint, then only 3n — m coordinates are independent, and the system is said to possess S = 3n — m degrees of freedom. We give the name generalized coordinates to any set of S independent quantities that completely specifies the state of a system (their number equals the number of degrees of freedom). The generalized coordinates are noted q1, q2, . . . , or simply as the qj. A set of independent generalized coordinates In certain cases, we use generalized coordinates which number exceeds the number of degrees of freedom and we explicitly take into account the constraint relations through the use of the Lagrange undetermined multipliers. Such would be the case, for example, if we desired to calculate the forces of constraint. The choice of a set of generalized coordinates to describe a system is not unique. We choose the set that gives the simplest equations of motion. , the time derivatives of qj, are called the generalized velocities. Important Notes on Notation Cartesian coordinates are noted Generalized coordinates are noted (designates the particle) q j , j 1, 2,...s , s number of degres of freedom The index i is reserved for Cartesian coordinates. xi , for i = 1,2,3 , represents either x, y, or z depending on the value of i . The index α will be used to identify quantities associated with a given particle when using Cartesian coordinates. For example, the position vector for particle α is given by rα, and its kinetic energy Tα Einstein’s summation convention: Whenever an index appears twice (an only twice), then a summation over this index is implied. For example, Lagrange’s equations of motion in generalized coordinates In general, the relationships linking the Cartesian and generalized coordinates and velocities can be expressed as We may also write the inverse transformations as Also, there are m equations of constraint of the form It follows naturally that Hamilton’s Principle can now be expressed in term of the generalized coordinates and velocities as [5] with Lagrange’s equations given by [6] if we refer to the definitions of the quantities in chapter 2 and make the identifications: Study Examples 7.1 and 7.3 from the textbook. Eg 7.3: see textbook Other example: The double pendulum. Consider the case of two particles of mass m1 and m2 each attached at the end of a mass less rod of length l1 and l2 , respectively. The second rod is also attached to the first particle (see Figure ). Derive the equations of motion for the two particles. Solution: It is desirable to use cylindrical coordinates for this problem. We have two degrees of freedom, and we will choose θ1 and θ2 as the generalized coordinates. Starting with Cartesian coordinates, we write an expression for the kinetic and potential energies for the system (take U=0 at y=0). And from Lagrange’s equations we get or Lagrange’s equations with undetermined multipliers If the constraint relations for a problem are given in differential form, we can incorporate them directly into Lagrange's equations by using the Lagrange undetermined multipliers (see Chapter 2) That is, for constraints expressible as [7] the Lagrange equations (see chap 2) are [8] The undetermined multipliers constraint. k (t ) are closely related to the forces of The generalized forces of constraint Qj are given by [9] Study Example 7.9 from the textbook. (see textbook) Equivalence of Lagrange’s and Newton’s equations We now explicitly demonstrate the equivalence of Lagrange’s and Newton’s equations. Let us choose the generalized coordinates to be the rectangular coordinates. Lagrange's equations (for a single particle) then become We also have: for a conservative system: [10] and so Lagrange’s Equations yield the Newtonian equations, as required: A theorem concerning the kinetic energy In a Cartesian coordinates system the kinetic energy of a system of particles is expressed as where a summation over i is implied. Using equations relating the two systems of coordinates: An important case occurs when a system is scleronomic, i.e., there is no explicit dependency on time in the coordinate transformation, we then have and the kinetic energy can be written in the form [11] where a summation on i is still implied We see that the kinetic energy is also a quadratic function of the (generalized) velocities. If we next differentiate equation [11] with respect to ql and then multiply it by (and summing), we get ql [12] Conservation theorems Consider a general Lagrangian L; the total time derivative of L is (there is summation on j) But from Lagrange’s equations, [13] where we have introduced a new function H called the Hamiltonian of the system [14] In cases where the Lagrangian is not explicitly dependent on time we find that dH 0 H cste. [15] dt If we are in presence of a scleronomic system, then Equation [15] can be written as (from [12]) The Hamiltonian of the system is equaled to the total energy only if the following conditions are met: 1. The system is scleronomic; ie the equations of the transformation connecting the Cartesian and generalized coordinates must be independent of time (the kinetic energy is then a quadratic function of the generalized velocities). 2. The potential energy must be velocity independent. The Hamiltonian of the system is conserved (but not necessarily equal to the total energy) when the Lagrangian is not explicitly dependent on time. Canonical equations of motion – Hamiltonian mechanics. if the potential energy of a system is velocity independent, then the linear momentum components in rectangular coordinates are given by By analogy, in the case in which the Lagrangian is expressed in generalized coordinates, we define the generalized momenta as [16] The Lagrange equations of motion are then expressed by [17] Using the definition [16] of the generalized momenta, Equation [14] for the Hamiltonian may be written as From [16], the generalized velocities can be expressed as Thus we may make a change of variables from the set to the set and express the Hamiltonian as [18]