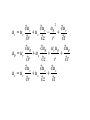Download ent 153_bernoulli equation

Fluid Kinematics
• Fluid kinematics refers to features of a
fluid in motion.
• Consideration of velocity, acceleration,
flow rate, nature of flow and flow
visualisation are taken up in fluid
kinematics.
There are two ways to analyse fluid motion:
1)
Lagrangian method, and 2) Eulerian method
In the Lagrangian method, a particle or an element of fluid is identified
and followed during the course of motion with time, as shown in Fig.
1.
•
The identified lump of fluid may change in shape, size and state as it
moves.
•
The laws of Mechanics must be applied to it at all times.
u  u ( x, y, z, t ); v  v( x, y, z, t )
z  z ( x, y , z , t )
•
•
Difficulty in tracing the lump of fluid rules out the possibility of applying
the Lagrangian approach
In the Eulerian method, the fluid is observed by setting up fixed
stations or observatories in the flow field. Motion of the fluid is
specified by velocity components expressed as functions of space
and time,
• In the Eulerian approach, the fluid motion at all points in the flow
field is determined by applying the laws of mechanics at all fixed
stations.
• This is considerably easier than the Lagrangian approach and is
followed in the study of Fluid Mechanics.
Dimensions of Flow
A fluid flow is said to be one, two, or three dimensional depending
upon the number of independent space coordinates, i.e. one, two, or
three respectively, required to describe the flow.
One dimensional Flow: When the dependent variables are functions
of only one space coordinate, say x, it is one dimensional flow.
Examples: Flow through pipes, channels and variable area ducts if
the velocity distribution is considered constant at each cross section.
Dependent variables such as velocity, pressure, density,
temperature vary only with x, the only independent variable in one
dimensional flow as shown in Fig. 2.
The axis of the passage does not have to be a straight line for a flow
to be one dimensional. For example, the flow shown in Fig. 2(b) is
one dimensional if s, the streamwise direction is chosen as the
independent coordinate.
The axis of the passage does not have to be a straight line for a flow to
be one dimensional. For example, the flow shown in Fig. 2(b) is one
dimensional if s, the streamwise direction is chosen as the independent
coordinate.
Two dimensional Flow:
When the dependent variables in a fluid flow vary with only two
space coordinates, the flow is said to be two dimensional. The flow
does not vary along the third coordinate direction
Example: The flow around a circular cylinder of infinite length (as
shown in Fig. 2c) is two dimensional in the x-y plane.
Axisymmetric Flow: A flow is said to be axisymmetric if the velocity
profile is symmetrical about the axis of symmetry. In other words, the
velocity profile is the same at different diametral planes drawn
through the passage.
Example: Velocity profiles at two locations for an axisymmetric flow
through a conical passage are shown in Fig. 2(d).
Steady Flow: If the dependent fluid variables at any point in the flow
do not change with time, the flow is said to be steady flow. Thus

(dependent fluid var iables )  0
t
u v w
p 
 
0
 ,etc
t t t
t t
It follows that

(dependent fluid var iables )  0
t
Unsteady Flow: If the dependent fluid variables change with the
passage of time at a position in the flow, the flow is called unsteady
flow. Thus
• Steadiness of flow means that the flow-pattern does not change
with time whereas unsteadiness refers to changing flow-pattern with
the passage of time at the same point in space.
Uniform Flow: If the velocity, in magnitude, direction and sense is
identical throughout the flow field, the flow is said to be uniform
flow. This requires the velocity components to be the same at
different positions in the flow.
In other words, the space rate of change of velocity components at
that time must vanish.
It follows that

(dependent fluid var iables )  0
s
u
u u v v w
 0      , etc
x
y z x y y
for uniform flow.
It is conventional to define the term “uniform flow” only
in terms of the velocity components rather than in
terms of other dependent fluid variables.
Further, a flow may be considered uniform over the
cross sections although it may not be uniform
longitudinally.
Non-uniform Flow: If the velocity components at
different locations are different at the same instant of
time, the flow is said to be non-uniform.
Note: Steadiness refers to ‘no change with time’ and
uniformity refers to ‘no change in space’. Therefore, a
flow can be steady or unsteady quite independent of
its being uniform or non-uniform. All the four
combinations are possible.
Acceleration in Fluid Flow: The velocity components in a fluid
flow are, in general, functions of space and time
u  u ( x, y, z , t ), v  v( x, y, z , t ),
w  w( x, y, z , t )
From differential calculus, an infinitesimal change in u is given by
u
u
u
u
du  dx  dy  dz  dt
x
y
z
t
And the acceleration components are given by
du Du
u u
u u
ax  
u v w 
dt Dt
x y
z t
dv Dv
v v
v v
ay  
u v w 
dt Dt
x y
z t
dw Dw
w w
w w
az  
u v w 
dt Dt
x
y
z t
Total acceleration = Convective acceleration + Local
acceleration
Total acceleration is also called as substantial, material or
particle derivative.
• For steady flow: Only Local acceleration components are zero.
• For uniform flow: Only Convective acceleration components
vanish.
• For steady uniform flow: Total acceleration becomes zero and
the flow is non-accelerating in space and time.
Expressions for the components of acceleration in cylindrical
coordinates for an axisymmetric flow are given below:
ur
ur u
ur
ar  u r
 uz


r
z
r
t
u
u ur u u
a  ur
 uz


r
z
r
t
u z
u z u z
a z  ur
 uz

r
z
t
2
Streamlines, Pathlines and Streaklines
A streamline in a fluid flow is a line tangent to which at any point is
in the direction of velocity at that point at that instant.
• Streamlines are, therefore, equivalent to an instantaneous snap-shot
indicating the directions of velocity in the entire flow field as shown
in Fig. 4(a) and (b).
• There can be no flow across a streamline since the component of
velocity normal to a streamline is zero.
• A streamline cannot intersect itself nor can any streamline intersect
another streamline.
• In steady flow, the same streamline-pattern should hold at all times,
since the velocity vector cannot change with time.
Consider, first a streamline in a plane flow in the x-y plane as shown
in Fig. 3. By definition, the velocity vector U at a point P must be
tangential to the streamline at that point. It follows that
dy/dx = tan θ = v/u or u dy – v dx = 0
where u and v are the velocity components along x and y directions
respectively.
It may also be noticed that the velocity vector is expressed as
U = U (s, t)
which shows that the velocity may vary along a streamline direction
s as well as with the passage of time.
Consider next an elementary displaced element δs along a general
streamline where the velocity is U such that
U = u i+ v j + w k
and
δs = δx i+ δy j + δz k
By the definition of a streamline, U must be directed along δs. For
collinear vectors, the cross product must vanish.
Hence,
U x δs = 0
i
j
k
u v
w 0
x y z
Or,
(vδz – wδy) i– (uδz – wδx) j + (uδy – vδx) k = 0
δx/u = δy/v = δz/w
whence
which is the equation of a streamline in a three dimensional flow,
steady or unsteady, uniform or non-uniform, viscous 0r inviscid,
compressible or incompressible.
A strteam surface is generated by a large number of closely
spaced streamlines which pass through an arbitrary curve AB as
in Fig. 4(c).
•
A stream surface can be plane, axisymmetric or spatial.
•
If the arbitrary line constitutes a closed curve, e.g., ABCD
as in Fig. 4(d), the closely spaced
streamlines passing
through the curve constitute a tubular stream surface called a
stream tube.
•
No flow can penetrate a stream surface or a stream tube.
•
•
•
•
A pathline in a fluid flow is the trajectory of a fluid particle, say P1 as
it advances with the passage of time, say from ti to final time tf as in
Fig. 4(e).
Pathlines are, therefore, history lines of individual fluid particles
over a period of time.
Tangent at a point on a pathline must be in the direction of
velocity at that point at the time
when the particle passes that
point.
A pathline, therefore, intersect itself at different times and in
general pathlines may
constitute a pattern of intersecting zigzag lines.
In steady flow, the streamlines and pathlines coincide.
A streakline is the locus of locations, Fig. 4(f), at an instant of time,
of all the fluid particles that have passed through a fixed point in a
flow field.
A little consideration will show that the streamlines, pathlines and
streaklines are coincident in a steady flow.
Law of Conservation of mass: Conservation of mass or
Continuity Equation
• Consider a control volume within the boundary layer as shown
in Fig. 7(b) and assume that steady state conditions prevail.
• There are no gradients in the z direction and the fluid is
incompressible.
Rate of mass flow out of the
C.V. in the y-direc.ion
Rate of mass flow into the
control volume in the xdirection
7
Rate of mass flow out of the
control volume in the xdirection
Rate of mass flow into the C.V. in the
y-direction
7
From Fig. 7, the net mass flow into the element in the x direction is,
u
  dxdy
x
Similarly, the net mass flow into the control volume in the y direction is,
v

dydx
y
Since the net mass flow rate out of the control volume must be zero, we
obtain
u v
  (  )dxdy  0
x y
From which it follows that in two-dimensional steady flow, conservation of
mass requires that
u v

0
x y
(13)
Example:
Does a velocity field given by
U = 5 x3 i – 15 x2 y j +t k
Represent a possible fluid motion of an incompressible fluid ?
Example:
Two components of velocity in an incompressible fluid flow are given by
u = x3 – y3
and
v = z3 – y3
Determine the third component, assuming that the origin is a stagnation
point.
Example:
Do the following velocity components represent a possible flow ?
Discuss the possibilities.
u = 2 x + 3 y and v = 3 y – 4 x.
Kinematics of a Fluid element
A fluid element may move in a flow and undergo
(a) Pure or irrotational translation
(b) Pure rotation or rotational translation
(c) Pure distortion or deformation; angular or linear.
These are illustrated in Fig. 9 (a), (b) and (c) respectively by
taking an upright cubical fluid element to start with in each case.
Irrotational Flow
• For irrotational flow, each component of rotation
or of vorticity (rotation = ½ vorticity) must vanish,
i.e., ωx = 0 = ωy = ωz.
• In particular, for plane flow in x-y plane,
•
δu/δy - δv/δx = 0
is the condition of irrotationality.
• EULER’S EQUATION OF MOTION ALONG A STREAMLINE
To derive a relation between velocity, pressure, elevation and
density along a streamline.
• Fig. shows a short section of a streamtube surrounding the
streamline and having a small cross sectional area so that
velocity be considered constant over the cross section.
• AB and CD are two cross sections separated by a short
distance δs.
• At AB, the area is A, velocity v, pressure p and elevation z, while
at CD, the corresponding values are, A+ δA, v+ δv, p+ δp and z+
δz.
• The surrounding fluid will exert a pressure pside on the sides of
the element.
• The fluid is assumed to be inviscid. Thus, there will be no shear
stresses on the sides of the element and pside will act normally.
• The weight of the element mg will act vertically downward at an
angle θ to the streamline.
Mass per unit time flowing
= ρAv
Rate of increase of momentum from AB to CD = ρAv[(v+ δv) – v)] =
ρAv δv
The forces acting to produce this increase of momentum in the
direction of motion are:
Force due to p in direction of motion
= pA
Force due to p+ δp opposing motion
= (p+ δp)(A+ δA)
Force due to pside producing a component
In the direction of motion
= pside δA
Force due to mg producing a component
Opposing motion
= mgcosθ
Resultant force in the direction of motion pA – (P+ δp)(A+ δA)+pside
δA-mgcosθ
The value of pside will vary from p at AB to p+ δp at CD and can be
taken up as p+k δp, where k is a fraction.
Weight of element, mg = ρg*Volume = ρg(A+½ δA) δs,
cosθ = δz/ δs
Resultant force in the direction of motion = -p δA – A δ p - δp δA + p
δA + k δp. δA – ρg(A+½ δA) δs.(δz/ δs)
Neglecting products of small quantities,
Resultant force in the direction of motion = -A δp - ρgA δz
Applying Newton’s second law of motion, we get,
ρAv δv = -A δp - ρgA δz
Dividing by ρAδs, we get
1 p
v
z
v  g  0
 s
s
s
Or in the limit as δs
0,
1 dp
dv
dz
v  g
0
 ds
ds
ds
(A)
• This is known as Euler’s Equation, giving, in differential form,
the relationship between pressure p, velocity v, density ρ
and elevation z along a streamline for steady flow.
v2
  gz  const
 2
p
• It cannot be integrated until the relationship between density ρ and
pressure p is known.
• For an incompressible flow, for which ρ is constant, integration of
the above equation (A) along the streamline, w.r.t. to s, gives
p
v2

 z  const
g 2 g
• In which the terms represent the energy per unit weight. The
above equation is known as Bernoulli’s Equation and states
the relationship between pressure, velocity and elevation for
steady flow of a frictionless fluid of constant density
• An alternative form is:
v2

 gz  const
 2
p
In which the terms represent the energy per unit volume.
• These equations apply to a single streamline. The sum of the three
terms is constant along any streamline, but the value of the constant
may be different for different streamlines in a given stream.
• If the earlier integration of Equation (A) is carried along the
streamline between any two points indicated by suffixes 1 and 2,
2
2
then
p1 v1
p2 v2

 z1 

 z2
g 2 g
g 2 g
• For a compressible fluid, the integration of Equation (A) can only be
partially completed, to give

dp
v2

z H
g
2g
• Euler’s Equation of Motion
•
Let us obtain the Euler’s momentum equation for two dimensional
inviscid steady flow in a vertical plane with reference to an elementary fluid
control volume in Figure below. The external forces acting on an element
are classified as surface forces and body forces.
• We use the term surface force = A force expressible
p + (∂p/∂z)δz
as a stress multiplied by the area of a surface
e.g. pressure force.
D
C
• We use the term body force = A force proportional
a
to the volume of the fluid element e.g. gravity force.
C
δz G
p
p + (∂p/∂x)δx
• With reference to the figure, the net surface force
B
In the x-direction = pzy  ( p  p x)zy
A
x
x
=  p xyz   p V
x
x
There is no body force in the x-direction.
p
δx
•
•
Similarly the net surface force plus the body force in the z-direction =
p

V  gV
z
Recalling the acceleration components for steady flow in the x-direction =
u
u
u
w
x
z
•
And the acceleration component for steady flow in the z-direction =
•
The Newton’s second law in the differential form can be written as
w
w
u
w
x
z
DU
dF  dm
 mass  total acceleration
Dt
• Therefore,
(u
(u
u
u
p
w
) V  
V along the x-axis
x
z
x
w
w
p
 w ) V   V  gV
x
z
z
along the z-axis
(1)
(2)
• Finally, for the two-dimensional steady flow of an inviscid fluid in a
vertical plane, the Euler’s momentum equations are:
And
u
u
1 p
(u
w )
x
z
 x
(u
(3)
w
w
1 p
w )
g
x
z
 z
(4)
Case (a): Along a streamline in an inviscid and steady flow
Multiply each term of equation (3) by x and each term of equation (4)
by z and adding them:
u
u
w
w
1  p
p 
u x  w x  u z  w z    x  z   gz
x
z
x
z
  x
z 

dp
 gdz
=

• The right hand side term of the above equation can be simplified as
follows:
• Using the equation of a streamline in the x-z plane:
uz  wx  0
or
uz  wx
The L.H.S. of equation (5) becomes:
 u 2  w2   V 2 
u
u
w
w
  d  
(u x  u z)  (w x  w z )  udu  wdw  d 
x
z
x
z
 2   2 
Thus, equation (5) becomes:
V 2 
dp

d


 gdz
 2 



Case (b) Between any two points in a Potential/Irrotational and
steady flow
Using the equation of irrotationality in the x-z plane,
u w

0
z x
or
u w

z
x
• The left hand side of equation (5) becomes:
u
w
u
w
x  w
x)  (u
z  w
z )
x
x
z
z
u   w
w 
 u
 u
x  u
z    w
x  w
z 
z
z
 x
  x

(u
 u 2  w2 
V 2 
  d 

 udu  wdw  d 
2


 2 
• Which is precisely the same as for the case (a).
Now, for either case (a) or case (b), it can be written as
V 2

 gdz  d 
 2


dp




• The assumption of two-dimensionality, as above, in case (a) or case (b)
is not necessary. It was made merely for the sake of reducing the
number of terms for convenience.
• Integration of the Euler’s equation results in the familiar form of the
BERNOULLI equation.
•
Or, on rearranging the terms and then integrating, we get:

p
V2

z 
g
2g
Constant
This is the general form of the Bernoulli equation, which may
now be simplified for different cases.
For an incompressible fluid flow, ρ = constant,
p
V2

 z Constant
g
2g
(ii) For a compressible fluid flow, undergoing an adiabatic process,
p  C

dp  C  1d
And
 1
  p 
dp 

p

 2



C

d


(
)(
)(
)


 g g 
g    1    1 g 
•
The Bernoulli equation appears as:

V2

 gz  K
 1 
2
•
•
•
•
•
•
•
•
p
The assumptions made in the derivation of the Bernoulli equation
may now be summarized as follows:
Inviscid flow
Steady flow
Either the flow is along a streamline or the flow is irrotational
Two-dimensional flow, in the presence of gravitational forces.
p V2

 z  is constant
For incompressible flow, the form
g 2 g
 p V2
For the compressible flow, the form is

 gz  K
 1  2
The Bernoulli equation may, therefore, be applied where these
assumptions can be justified.
Energy Analysis of Steady Flows
Where,hpump,u is the useful head delivered to the fluid by the pump.
h pump,u 
 pumpW pump
g
m

Where W
pump is Shaft Power input through the pump’s shaft.
Similarly hturbine,e is the extracted head removed from the fluid by the turbine.
Also,
hturbine,e
Wturbine

W
turbine

g
turbinem
Where,
is Shaft Power output through the turbine’s shaft. hL is the
irreversible head loss between 1 and 2 due to all components of the piping
system other than pump or turbine.
• Problem 1: The pump of Figure 1 is to increase the pressure of water
from 200 kPa to 600 kPa. If the pump efficiency is 85%, how much
electrical power will the pump require? The exit area is 20 cm above the
inlet area. Assume inlet and exit areas are equal.
• Problem 2: The venturimeter shown reduces the pipe diameter from 10
cm to a minimum of 5 cm (Fig. 2). Calculate the flow rate and the mass
flux assuming ideal conditions.