Download Chapter 8

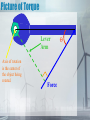
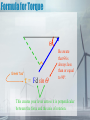
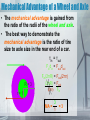
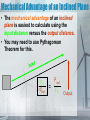
Chapter 8
Rotational Equilibrium and
Dynamics
Chapter 8 Objectives
• Define torque
• Identify the lever arm associated with the torque
of an object
• Identify the center of mass of an object
• Define second condition of equilibrium
• Recognize the moment of inertia of several
objects
• Identify the six types of simple machines.
• Explain how simple machines effect work
• Calculate mechanical advantage
Definition of Torque
• Torque is a quantity that measures the ability of a
force to rotate an object around some axis.
• Mr. Lent’s Definition – Torque is work in a circle.
• Torque depends on a force, a lever arm, and the
angle at which the force is applied.
• The lever arm is the perpendicular distance from
the axis of rotation to the line drawn along the
direction of the force.
• The sign on torque is based on the direction in
which the force causes the object to rotate.
• Rotation in a clockwise direction is negative and
counterclockwise is positive.
Picture of Torque
Lever
Arm
Axis of rotation
is the center of
the object being
rotated.
Force
Θ
Formula for Torque
Θ
Greek “tao”
τ = Fd sin Θ
Be aware
that Θ is
always less
than or equal
to 90o.
This creates your lever arm so it is perpendicular
between the force and the axis of rotation.
How to Find Θ
• Θ is an angle less than or
equal to 90o
• Extend the force vector
in either direction so that
it will create an acute
angel with the original
lever arm.
• You only need extend it
so you can draw a line
from the axis of rotation
to the force vector such
that the line is
perpendicular.
• That perpendicular line
is now your new lever
arm.
Θ
Θ
Center of Mass
• Center of mass is the point at which all the mass of a
body can be considered to be concentrated when
analyzing translational motion.
• The center of gravity is the point at which the force of
gravity acts on an object.
• In the higher levels of physics, center of mass and
center of gravity are two different concepts and
therefore can exist at two different locations of an
object.
• For our purposes, we will consider them to be the
same point in an object.
• For regularly shaped objects, such as a sphere, cube
or solid rod, the center of mass is located in the
geometric center of the object.
Moment of Inertia
• Remember back to Newton’s 1st Law of Motion,
Objects tend to stay in motion, or at rest, unless
acted upon by a net force.
• Notice it says Motion, but does not specify whether
the motion is linear or rotational.
• We also said that Newton’s 1st Law describes the
term inertia, or the the resistance of a change in
motion.
• The tendency of a body rotating about a fixed axis to
resist a change in rotational motion is called the
moment of inertia of an object.
• The moment of inertia of an object depends on the
mass of an object and how far away it is from the axis
of rotation.
• The general rule is that the further the mass is from
the rotating axis, the larger the magnitude for the
moment of inertia.
Calculating the Moment of Inertia of Common Shapes
Object
Picture
Formula
Characteristics
Thin hoop about the
symmetry axis
MR2
Thin hoop about the
diameter
½MR2
This is like a ring standing on its end and
spinning about the diameter.
Point mass about axis
MR2
This is spinning a weight on the end of a
string. Acts like thin hoop.
Disk or cylinder about
symmetry axis
½MR2
Flat plate or any solid cylinder, no matter
how long.
Thin rod through
center axis
1/
2
L is the total length of the rod and it
rotates like spinning a ruler on finger.
Thin rod about end of
rod
1/
2
Hold ruler at end and spin in a circle.
Solid sphere about the
diameter
2/
2
Spinning a bowling ball on your finger.
Spherical shell about
the diameter
2/ MR2
3
R is the radius of the hoop and M is the
total mass. Wedding ring.
12ML
3ML
5MR
Spinning a basketball on your finger.
Rotational Equilibrium
•Recall the 1st Condition of
Equilibrium is that the net
force on an object is equal
to 0.
•That is called translational
equilibrium.
•The word translation
means the refers to the
translation of an object
which only happens in a
straight line, or linear
path.
•Translational equilibrium
assures that the net
horizontal and the net
vertical forces sum to 0.
•We can now add the
2nd Condition of
Equilibrium.
•Rotational equilibrium
is achieved when the
net torque is equal to
0.
•So the sum of all
clockwise torques
should be equal to
the sum of all
counterclockwise
torques.
Newton’s 2nd Law of Rotation
• Recall Newton’s 2nd Law of Motion said
that F = ma.
• Since F can go in infinite directions
around a circle, we cannot use that
formula for rotational motion.
• But Torque is work directed in a circle,
which does account for force and its
direction.
Translational v Rotational
• We saw from section 8.2 that if the net
force was not equal to 0, rotation would
occur. And more torque would mean
faster rotation.
• If the speed of rotation changes that’s
called angular acceleration.
• But all of this depends on the object’s
shape and its mass.
• The only way to account for the mass of
the rotating object is to account for its
moment of inertia
So
τ
NET
= Iα
Comparing Translational and Rotational
•Translational is a
straight line
• F=ma
•Sign shows
direction
•Positive means
right/up
•Negative means
left/down
•Rotational is
circular
•τ
NET
= Iα
•Sign shows
direction
•Positive –
counterclockwise
•Negative –
clockwise
Angular Momentum
• Recall that translational momentum was
p=mv
• Objects still have momentum while
rotating
• We account for rotating mass by using
moment of inertia
• And velocity in a circle is called angular
velocity
Angular momentum
L=Iω
Conservation of Angular Momentum
• Translational momentum is conserved,
thus angular momentum is conserved
• That is why a figure skater pulls his/her
arms in order to spin faster.
• Be sure to match the proper moment of
inertia to the rotating object(s) in the
system
Rotational Kinetic Energy
• Imagine a bowling ball rolling down
an alley
• We know it has kinetic energy in a
straight line…
• But it also has rotational kinetic
energy as well as translational
kinetic energy
• The formulas look alike just use the
correct variables for the correct
situation.
K = 1/ Iω2
ROT
2
Translational and Angular Convservation
• If ever asked to find the net kinetic
energy or net momentum on an
object, you must
– Sum the translational and angular
kinetic energys.
• 1/2I
ω2 + ½mv2
– Sum the translational and angular
momentums.
•
Iω + mv
Simple Machines
A machine is an object that transmits or modifies force, usually by
changing the force applied to an object.
All machines that you may think of are actually combinations or
modifications of 6 fundamental types of machines called simple
machines. And those are broken down into 2 families.
Lever Family
Inclined Plane
1. Lever – Teeter Totter, 1. Inclined Plane – A
Baseball Bat, Broom,
slanted surface like
etc.
a wheel chair ramp.
2. Pulley – A rope being 2. Wedge – Two
pulled around a
inclined planes
wheel.
back to back.
3. Wheel and axle – A
3. Screw – An inclined
wheel attached to a
plane wrapped
smaller diameter rod.
around a cylinder.
Mechanical Advantage
• Because the purpose of simple
machines is to alter the direction
or magnitude of an input force,
then it must provide some type
of advantage to produce the
output force.
• That advantage is called
mechanical advantage.
• The mechanical advantage of a
machine is a ratio of the output
force to the input force.
• It can also be a ration of the
input distance to the output
distance, which a little
manipulation of the
conservation of rotational
equilibrium.
τ in = τout
Findin = Foutdout
din
dout
MA =
Fout
= F
in
Fout
Fin
din
=d
out
Lever
• A lever is a type of arm that includes a pivot
point, or fulcrum.
• There are 3 classes of levers based on the
orientation of the fulcrum, input, and output
forces.
• Examples of levers are teeter totters, baseball
bats, pry bars, bottle openers, golf clubs,
hockey sticks, wrenches, etc.
Classes of Levers
1st Class Lever – The input force and output force are on
opposite sides of the fulcrum and are directed in opposite
directions.
(Teeter Totter)
2nd Class Lever – The fulcrum is at one end of the lever with
the input force at the other end and the output force is in the
middle. Also, the forces are directed in the same direction.
(Wheel barrow)
3rd Class Lever – The fulcrum is at
one end of the lever with the output force
at the other end and the input force is in
the middle. Again, the forces are directed
in the same direction. (Baseball bat)
Mechanical Advantage of a Lever
• The mechanical advantage of a any lever is
found by conserving rotational equilibrium.
τin = τout
Findin = Foutdout
Pulley
• A pulley is a part of the lever family because it
uses a fulcrum to redirect the force.
Fulcrum
Fixed v Movable Pulleys
•The behavior of pulleys
can differ based on
whether the pulley can
move or not.
•A fixed pulley is one in
which the pulley itself is
attached to a wall or pole
and does not move when
the load is moved.
•These types of pulleys
are often used to redirect
the applied force.
•Therefore, a moveable
pulley is one in which the
pulley moves as the load
moves.
•These types of pulleys
are used to spread the
load out over an additional
“rope” in the system.
•This transforms the force
of the load into 2 equal
tensions that each carry
half the weight.
Mechanical Advantage of a Pulley
•For any fixed pulley, the
mechanical advantage is
1.
•It is 1 applied force (1
rope) redirected over the
pulley to provide an
advantage of pulling
versus pushing, or vice
versa.
•For any moveable pulley,
the mechanical advantage
is always 2.
•There is now 2 applied
forces that aid in lifting the
load.
–So the input force is cut in
half because it only has to
lift one of the two lifting
forces.
Complex Pulley Systems
• Easiest way to calculate mechanical advantage of a
complex pulley system is to identify the following:
– Load bearing ropes
• These are the ropes around a moveable pulley.
– Redirecting ropes
• These are the ropes around a fixed pulley.
• The mechanical advantage is the reciprocal of the
tension in the load bearing ropes.
MA = 2
MA = 2
MA = 3
MA = 3
MA = 4
Wheel and Axle
• A wheel and axle is much like two pulleys of
different sizes that spin together.
Wheel
Axle
Mechanical Advantage of a Wheel and Axle
• The mechanical advantage is gained from
the ratio of the radii of the wheel and axle.
• The best way to demonstrate the
mechanical advantage is the ratio of tire
size to axle size in the rear end of a car.
τin = τout
Findin = Foutdout
R=3
r=1
Fin(2πR) = Fout(2πr)
(2πR) = Fout
(2πr) Fin
3
MA =
1
=3
Inclined Plane
• An inclined plane is simply a flat surface that is
used to move an object up or down an incline, or
elevation.
• The surface does not necessarily have to be flat,
it must be able to be modeled flat. (ie: a set of
stairs)
Mechanical Advantage of an Inclined Plane
• The mechanical advantage of an inclined
plane is easiest to calculate using the
input distance versus the output distance.
• You may need to use Pythagorean
Theorem for this.
din
dout
Fout
= F
in
Output
Wedge
• A wedge is two inclined planes placed back to
back.
• The most common form of a wedge is an ax.
Mechanical Advantage of a Wedge
• The mechanical advantage of a wedge is the ratio of
inclined surface to width of the wedge.
• It is very similar to the mechanical advantage of an
inclined plane.
• You might think that since a wedge is two inclined planes,
its mechanical advantage would be twice as large. But it
is spread over two surfaces so it divides the two back out.
• Notice that to increase the mechanical advantage of the
wedge, simply make the width smaller. That is why a
sharp knife is better than a dull knife!
Inclined Surface
Width
Screw
• As simply put as possible, a screw is an inclined
plane wrapped around a cylinder.
• It resembles a wheel and axle, except for the part
that is actually doing the work is the slope of the
threads of the screw.
Mechanical Advantage of a Screw
• The mechanical advantage of a screw is hard to
visualize, and therefore tricky to calculate.
• Avoiding all of the nasty calculation, it is a ratio of
the circumference of the screw divided by its
pitch.
• Pitch is the distance between threads.
• If you think about it, one turn will make the screw
go into the wood the same depth that one thread
of revolution. So that is how we get the
mechanical advantage.
Circumference of Screw
MA =
Pitch