Download Chapter 8:

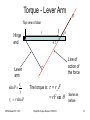
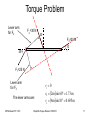
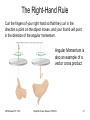
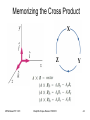
Chapter 8
Torque and Angular
Momentum
Torque and Angular Momentum
• Rotational Kinetic Energy
• Rotational Inertia
• Torque
• Work Done by a Torque
• Equilibrium (revisited)
• Rotational Form of Newton’s 2nd Law
• Rolling Objects
• Angular Momentum
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
2
Rotational KE and Inertia
For a rotating solid body:
K rot
n
1
1
1
1
2
2
2
 m1v1  m2 v2    mn vn   mi vi2
2
2
2
i 1 2
For a rotating body vi = ri where ri is the distance from the
rotation axis to the mass mi.
1
1 n
1 2
2
2 2
  mi ri     mi ri   I
2  i 1
2
i 1 2

n
K rot
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
3
Moment of Inertia
The quantity
n
I   mi ri
2
i 1
is called rotational inertia or moment of inertia.
Use the above expression when the number of masses that make
up a body is small. Use the moments of inertia in the table in the
textbook for extended bodies.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
4
Moments of Inertia
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
5
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
6
Moment of Inertia
Example: The masses are m1 and m2 and they are separated
by a distance r. Assume the rod connecting the masses is
massless.
Q: (a) Find the moment of inertia of the system below.

m1
r1
MFMcGraw-PHY 1401
r2
m2
r1 and r2 are the distances
between mass 1 and the
rotation axis and mass 2
and the rotation axis (the
dashed, vertical line)
respectively.
Chap08b-Torque-Revised 7/5/2010
7
Moment of Inertia-Axis Dependent
Take m1 = 2.00 kg, m2 = 1.00 kg, r1= 0.33 m , and r2 = 0.67 m.
2
I   mi ri 2  m1r12  m2 r22
i 1
 2.00 kg 0.33 m   1.00 kg 0.67 m 
2
2
 0.67 kg m 2
(b) What is the moment of inertia if the axis is moved so that is passes
through m1?
2
I   mi ri 2  m1r12  m2 r22
i 1
 2.00 kg 0.00 m   1.00 kg 1.00 m 
2
2
 1.00 kg m 2
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
8
Moment of Inertia
What is the rotational inertia of a solid iron disk of mass 49.0
kg with a thickness of 5.00 cm and a radius of 20.0 cm, about
an axis through its center and perpendicular to it?
From the table:
1
1
2
2
I  MR  49.0 kg 0.2 m   0.98 kg m 2
2
2
The moment of inertia involves the mass, the square of a
characteristic length, perpendicular to the axis of rotation,
and a dimensionless factor β.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
9
Torque
A torque is caused by the application of a force, on an
object, at a point other than its center of mass or its pivot
point.
hinge
Q: Where on a door do you
normally push to open it?
P
u
s
h
A: Away from the hinge.
A rotating (spinning) body will continue to rotate unless it
is acted upon by a torque.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
10
Torque - Force Components
Torque method 1:
Top view of door
F
F

Hinge
end
F||
  rF
r = the distance from the rotation axis (hinge) to the point
where the force F is applied.
F is the component of the force F that is perpendicular
to the door (here it is Fsin).
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
11
Torque
The units of torque are Newton-meters (Nm)
(not joules!).
By convention:
• When the applied force causes the object to
rotate counterclockwise (CCW) then  is positive.
• When the applied force causes the object to
rotate clockwise (CW) then  is negative.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
12
Torque
Torque method 2:
  r F
r is called the lever arm and F is the magnitude
of the applied force.
Lever arm is the perpendicular distance to the
line of action of the force.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
13
Torque - Lever Arm
F
Top view of door
Hinge
end

r

Line of
action of
the force
Lever
arm
r
sin  
r
r  r sin 
MFMcGraw-PHY 1401
The torque is: 
 r F
 rF sin 
Chap08b-Torque-Revised 7/5/2010
Same as
before
14
Torque Problem
The pull cord of a lawnmower engine is wound around a drum of
radius 6.00 cm, while the cord is pulled with a force of 75.0 N to start
the engine.
What magnitude torque does the cord apply to the drum?
F=75 N
R=6.00 cm
MFMcGraw-PHY 1401
  r F
 rF
 0.06 m 75.0 N   4.5 Nm
Chap08b-Torque-Revised 7/5/2010
15
Torque Problem
Calculate the torque due to the three forces shown about the left end of
the bar (the red X). The length of the bar is 4m and F2 acts in the middle
of the bar.
F2=30 N
30
F3=20 N
45
10
X
F1=25 N
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
16
Torque Problem
Lever arm
for F2
45
F2=30 N
30

F3=20 N
10

X
F1=25 N
Lever arm
for F3
r1  0
The lever arms are:
MFMcGraw-PHY 1401
r2  2m sin 60  1.73 m
r3  4m sin 10  0.695 m
Chap08b-Torque-Revised 7/5/2010
17
Torque Problem
1  0
The torques are:  2  1.73 m 30 N   51.9 Nm
 3  0.695 m 20 N   13.9 Nm
The net torque is +65.8 Nm and is the sum of the above
results.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
18
Work done by the Torque
The work done by a torque  is
W   .
where  is the angle (in radians) that the
object turns through.
Following the analogy between linear and rotational motion:
Linear Work is Force x displacement. In the rotational picture
force becomes torque and displacement becomes the angle
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
19
Work done by the Torque
A flywheel of mass 182 kg has a radius of 0.62 m (assume the
flywheel is a hoop).
(a) What is the torque required to bring the flywheel from rest to a
speed of 120 rpm in an interval of 30 sec?
 f  120
rev  2 rad  1 min 


  12.6 rad/sec
min  1 rev  60 sec 
  
  rF  r ma  rmr   mr 

 t 
 f  i 
f 
2
2
  mr 
  29.4 Nm
 mr 
 t 
 t 
2
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
20
Work done by the Torque
(b) How much work is done in this 30 sec period?
W     av t 
 i   f
  
 2
MFMcGraw-PHY 1401

f
t   

 2

t  5600 J

Chap08b-Torque-Revised 7/5/2010
21
Equilibrium
The conditions for equilibrium are:
F  0
τ  0
Linear motion
Rotational motion
For motion in a plane we now have three
equations to satisfy.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
22
Using Torque
A sign is supported by a uniform horizontal boom of length 3.00 m
and weight 80.0 N. A cable, inclined at a 35 angle with the boom,
is attached at a distance of 2.38 m from the hinge at the wall. The
weight of the sign is 120.0 N.
What is the tension in the
cable and what are the
horizontal and vertical
forces exerted on the boom
by the hinge?
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
23
Using Torque
This is important! You
need two components
for F, not just the
expected perpendicualr
normal force.
FBD for the bar:
y
Fy
T
X

Fx
x
wbar
Apply the conditions for
equilibrium to the bar:
Fsb
(1)  Fx  Fx  T cos   0
(2)  Fy  Fy  wbar  Fsb  T sin   0
L
(3)    wbar    Fsb L   T sin  x  0
2
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
24
Using Torque
Equation (3) can be solved for T:
L
wbar    Fsb L 
2
T
x sin 
 352 N
Equation (1) can be solved for Fx:
Fx  T cos   288 N
Equation (2) can be solved for Fy:
MFMcGraw-PHY 1401
Fy  wbar  Fsb  T sin 
Chap08b-Torque-Revised 7/5/2010
 2.00 N
25
Equilibrium in the Human Body
Find the force exerted by the biceps muscle in holding a one
liter milk carton with the forearm parallel to the floor.
Assume that the hand is 35.0 cm from the elbow and that
the upper arm is 30.0 cm long.
The elbow is bent at a right angle and one tendon of the
biceps is attached at a position 5.00 cm from the elbow and
the other is attached 30.0 cm from the elbow.
The weight of the forearm and empty hand is 18.0 N and the
center of gravity is at a distance of 16.5 cm from the elbow.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
26
MCAT type problem
y
Fb
“hinge”
(elbow
joint)
x
w
  F x  wx
b 1
Fb 
MFMcGraw-PHY 1401
2
Fca
 Fca x3  0
wx2  Fca x3
 130 N
x1
Chap08b-Torque-Revised 7/5/2010
27
Newton’s 2nd Law in Rotational
Form
  I
Compare to
MFMcGraw-PHY 1401
 F  ma
Chap08b-Torque-Revised 7/5/2010
28
Rolling Object
A bicycle wheel (a hoop) of radius 0.3 m and mass 2 kg is rotating
at 4.00 rev/sec. After 50 sec the wheel comes to a stop because
of friction.
What is the magnitude of the average torque due to frictional
forces?
  I  MR 
2
rev  2 rad 
i  4.00

  25.1 rad/sec
sec  1 rev 
f  0
  f  i


 0.50 rad/s 2
t
t
 av  MR 2   0.09 Nm
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
29
Rolling Objects
An object that is rolling combines translational motion (its center
of mass moves) and rotational motion (points in the body rotate
around the center of mass).
For a rolling object:
K tot  K T  K rot
1 2 1 2
 mvcm  I
2
2
If the object rolls without slipping then vcm = R.
Note the similarity in the form of the two kinetic energies.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
30
Rolling Example
Two objects (a solid disk and a solid sphere) are rolling down a ramp.
Both objects start from rest and from the same height.
Which object reaches the bottom of the ramp first?
h

This we know - The object with the largest linear velocity (v) at
the bottom of the ramp will win the race.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
31
Rolling Example
Apply conservation of mechanical energy:
Ei  E f
U i  Ki  U f  K f
1 2 1 2 1 2 1 v
mgh  0  0  mv  I  mv  I  
2 R
2
2
2
2
I 
1
mgh   m  2 v 2
R 
2
Solving for v:
MFMcGraw-PHY 1401
2mgh
v
I 


m

2 
R 

Chap08b-Torque-Revised 7/5/2010
32
Rolling Example
Example continued:
1
mR 2
2
2
I sphere  mR 2
5
I disk 
The moments of inertia are:
4
gh
For the disk: vdisk 
3
10
gh
For the sphere: vsphere 
7
Note that
the mass
and radius
are the
same.
Since Vsphere> Vdisk the
sphere wins the race.
Compare these to a box sliding down the ramp. vbox  2 gh
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
33
The Disk or the Ring?
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
34
How do objects in the previous example roll?
Both the normal force and the weight
act through the center of mass so
FBD:
y
N
 = 0.
This means that the object cannot
rotate when only these two forces
are applied.
w
x
The round object won’t rotate, but most students have difficulty
imagining a sphere that doesn’t rotate when moving down hill.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
35
Add Friction
y
  F r  I
 F  w sin   F  ma
 F  N  w cos  0
s
FBD:
N
Fs
x
s
cm
y

Also need acm = R and
w
x
v 2  v02  2ax
The above system of equations can be solved for v at the bottom of the
ramp. The result is the same as when using energy methods. (See text
example 8.13.)
It is the addition of static friction that makes an object roll.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
36
Angular Momentum
L
 net  lim
t 0 t
L  Iω
p
Fnet  lim
t 0 t
p  mv
Units of p are kg m/s
When no net external
forces act, the momentum
of a system remains
constant (pi = pf)
MFMcGraw-PHY 1401
Units of L are kg m2/s
When no net external
torques act, the angular
momentum of a system
remains constant (Li = Lf).
Chap08b-Torque-Revised 7/5/2010
37
Angular Momentum Example
A turntable of mass 5.00 kg has a radius of 0.100 m and spins with
a frequency of 0.500 rev/sec. Assume a uniform disk.
What is the angular momentum?
rev  2 rad 
  0.500

  3.14 rad/sec
sec  1 rev 
1
2
L  I   MR   0.079 kg m 2 /s
2

MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
38
Angular Momentum Example
A skater is initially spinning at a rate of 10.0 rad/sec with I=2.50 kg
m2 when her arms are extended.
What is her angular velocity after she pulls her arms in and
reduces I to 1.60 kg m2?
The skater is on ice, so we can ignore external torques.
Li  L f
I ii  I f  f
 Ii
 f  
If
MFMcGraw-PHY 1401

 2.50 kg m 2 
i  
 1.60 kg m 2 10.0 rad/sec   15.6 rad/sec




Chap08b-Torque-Revised 7/5/2010
39
The Vector Nature of Angular
Momentum
Angular momentum is a vector. Its
direction is defined with a right-hand rule.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
40
The Right-Hand Rule
Curl the fingers of your right hand so that they curl in the
direction a point on the object moves, and your thumb will point
in the direction of the angular momentum.
Angular Momentum is
also an example of a
vector cross product
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
41
The Vector Cross Product
The magnitude of C
C = ABsin(Φ)
The direction of C is
perpendicular to the
plane of A and B.
Physically it means
the product of A and
the portion of B that
is perpendicular to A.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
42
The Cross Product by Components
Since A and B are in the x-y plane A x B is along the z-axis.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
43
Memorizing the Cross Product
X
Z
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
Y
44
The Gyroscope Demo
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
45
Angular Momentum Demo
Consider a person
holding a spinning
wheel. When viewed
from the front, the
wheel spins CCW.
Holding the wheel horizontal, they step on to a platform
that is free to rotate about a vertical axis.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
46
Angular Momentum Demo
Initially there is no angular momentum about the vertical axis.
When the wheel is moved so that it has angular momentum
about this axis, the platform must spin in the opposite
direction so that the net angular momentum stays zero.
This is a result of conserving angular momentum.
Is angular momentum conserved about the
direction of the wheel’s initial, horizontal axis?
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
47
It is not.
The floor exerts a torque on the system (platform + person),
thus angular momentum is not conserved here.
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
48
Summary
• Rotational Kinetic Energy
• Moment of Inertia
• Torque (two methods)
• Conditions for Equilibrium
• Newton’s 2nd Law in Rotational Form
• Angular Momentum
• Conservation of Angular Momentum
MFMcGraw-PHY 1401
Chap08b-Torque-Revised 7/5/2010
49
X
Z
MFMcGraw-PHY 1401
Y
Chap08b-Torque-Revised 7/5/2010
50