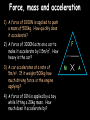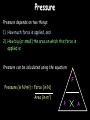* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download in m/s 2
Survey
Document related concepts
Transcript
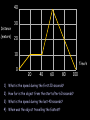
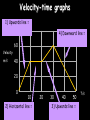
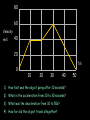
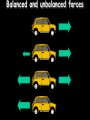
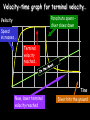
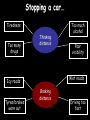
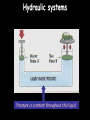
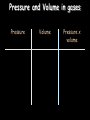
Motion Notes 2 Distance, Speed and Time Speed = (in m/s) D distance (in meters) time (in seconds) S T 1) Dave walks 200 meters in 40 seconds. What is his speed? 2) Laura covers 2km in 1,000 seconds. What is her speed? 3) How long would it take to run 100 meters if you run at 10m/s? 4) Steve travels at 50m/s for 20s. How far does he go? 5) Susan drives her car at 85mph (about 40m/s). How long does it take her to drive 20km? Distance-time graphs 2) Horizontal line = 40 4) Diagonal line downwards = 30 Distance (meters) 20 10 0 Time/s 20 1) Diagonal line = 40 60 80 100 3) Steeper diagonal line = 40 Distance (meters) 30 20 10 0 Time/s 20 40 60 80 100 1) What is the speed during the first 20 seconds? 2) How far is the object from the start after 60 seconds? 3) What is the speed during the last 40 seconds? 4) When was the object travelling the fastest? Speed vs. Velocity Speed is simply how fast you are travelling… This car is travelling at a speed of 20m/s Velocity is “speed in a given direction”… This car is travelling at a velocity of 20m/s east Acceleration Vf-Vi Acceleration = change in velocity (in m/s) (in m/s2) time taken (in s) A T 1) A cyclist accelerates from 0 to 10m/s in 5 seconds. What is her acceleration? 2) A ball is dropped and accelerates downwards at a rate of 10m/s2 for 12 seconds. How much will the ball’s velocity increase by? 3) A car accelerates from 10 to 20m/s with an acceleration of 2m/s2. How long did this take? 4) A rocket accelerates from 1,000m/s to 5,000m/s in 2 seconds. What is its acceleration? Velocity-time graphs 1) Upwards line = 80 Velocity m/s 4) Downward line = 60 40 20 0 10 2) Horizontal line = 20 30 40 50 3) Upwards line = T/s 80 60 Velocity m/s 40 20 0 T/s 10 20 30 40 1) How fast was the object going after 10 seconds? 2) What is the acceleration from 20 to 30 seconds? 3) What was the deceleration from 30 to 50s? 4) How far did the object travel altogether? 50 Balanced and unbalanced forces Consider a camel standing on a road. What forces are acting on it? Reaction These two forces would be equal – we say that they are BALANCED. The camel doesn’t move anywhere. Weight Balanced and unbalanced forces Reaction What would happen if we took the road away? Weight Balanced and unbalanced forces What would happen if we took the road away? The camel’s weight is no longer balanced by anything, so the camel falls downwards… Weight Balanced and unbalanced forces What would happen if we took the road away? The camel’s weight is no longer balanced by anything, so the camel falls downwards… Balanced and unbalanced forces 1) This animal is either ________ or moving with _____ _____… 3) This animal is getting _______…. 2) This animal is getting _________… 4) This animal is… Balanced and unbalanced forces Force and acceleration If the forces acting on an object are unbalanced then the object will accelerate, like these wrestlers: Force (in N) = Mass (in kg) x Acceleration (in m/s2) F M A Force, mass and acceleration 1) A force of 1000N is applied to push a mass of 500kg. How quickly does it accelerate? F 2) A force of 3000N acts on a car to make it accelerate by 1.5m/s2. How heavy is the car? 3) A car accelerates at a rate of 5m/s2. If it weighs 500kg how much driving force is the engine applying? 4) A force of 10N is applied by a boy while lifting a 20kg mass. How much does it accelerate by? M A Terminal Velocity Consider a skydiver: 1) At the start of his jump the air resistance is _______ so he _______ downwards. 2) As his speed increases his air resistance will _______ 3) Eventually the air resistance will be big enough to _______ the skydiver’s weight. At this point the forces are balanced so his speed becomes ________ - this is called TERMINAL VELOCITY Terminal Velocity Consider a skydiver: 4) When he opens his parachute the air resistance suddenly ________, causing him to start _____ ____. 5) Because he is slowing down his air resistance will _______ again until it balances his _________. The skydiver has now reached a new, lower ________ _______. Velocity-time graph for terminal velocity… Parachute opens – diver slows down Velocity Speed increases… Terminal velocity reached… Time New, lower terminal velocity reached Diver hits the ground Weight vs. Mass Earth’s Gravitational Field Strength is 10N/kg. In other words, a 1kg mass is pulled downwards by a force of 10N. W Weight = Mass x Gravitational Field Strength (in N) (in kg) (in N/kg) M g 1) What is the weight on Earth of a book with mass 2kg? 2) What is the weight on Earth of an apple with mass 100g? 3) Dave weighs 700N. What is his mass? 4) On the moon the gravitational field strength is 1.6N/kg. What will Dave weigh if he stands on the moon? Friction 1) What is friction? 2) Give 3 examples where it is annoying: 3) Give 3 examples where it is useful: 4) What effect does friction have on the surfaces? Stopping a car… Tiredness Too many drugs Thinking distance Poor visibility Wet roads Icy roads Tyres/brakes worn out Too much alcohol Braking distance Driving too fast Work done When any object is moved around work will need to be done on it to get it to move (obviously). We can work out the amount of work done in moving an object using the formula: Work done = Force x distance moved in J in N W in m F D Kinetic energy Any object that moves will have kinetic energy. The amount of kinetic energy an object has can be found using the formula: Kinetic energy = ½ x mass x velocity squared in J in kg KE = ½ in m/s mv2 Some example questions… 1) A 70kg boy is running at about 10m/s. What is his kinetic energy? 2) A braking force of 1000N is applied by a driver to stop his car. The car covered 50m before it stopped. How much work did the brakes do? 3) What is the kinetic energy of a 100g tennis ball being thrown at a speed of 5m/s? 4) A crane is lifting a 50kg load up into the air with a constant speed. If the load is raised by 200m how much work has the crane done? (The answer isn’t 10,000J) Pressure – some basic ideas Describe and draw experiments for each of the following ideas: 1) Pressure increases with depth 2) Pressure is the same in all directions at a certain depth Pressure Pressure depends on two things: 1) How much force is applied, and 2) How big (or small) the area on which this force is applied is. Pressure can be calculated using the equation: F Pressure (in N/m2) = Force (in N) Area (in m2) P A Some example questions… 1) A circus elephant weighs 10,000N and can stand on one foot. This foot has an area of 50cm2. How much pressure does he exert on the floor (in N/cm2)? 2) A 50kg woman copies the elephant by standing on the heel of one of her high-heeled shoes. This heel has an area of 1cm2. How much pressure does she exert on the floor? Work through q2 on p58 Extension task: Atmospheric pressure is roughly equivalent to 1kg pressing on every square centimetre on our body. What does this equate to in units called Pascals? (1 Pascal = 1N/m2) Hydraulic systems Hydraulic systems Pressure is constant throughout this liquid Hydraulic systems Basically, a smaller force on piston A will produce a larger force on piston B because the pressure of the liquid is constant. Magic! 1) If the area of piston A is 5cm2 and piston B is 20cm2 how much will the force be multiplied by? 2) If the area of the slave piston is ten times bigger than the master piston what force will be needed to lift an object weighing 1000N? 3) A force of 10N is used to lift a weight of 50N. What is the ratio of the master piston area to the slave piston area? Pressure and Volume in gases Pressure Volume Pressure x volume Pressure and volume in gases Conclusion When we multiplied the pressure of a gas by its volume we found that the answer was always __ _______. In other words, if you DECREASE the volume you _______ the pressure and so on. “One goes up, the other goes down” Pressure and Volume in gases This can be expressed using the equation: Initial Pressure x Initial Volume = Final Press. x Final Vol. PIVI = PFVF 1) A gas has a volume of 3m3 at a pressure of 20N/m2. What will the pressure be if the volume is reduced to 1.5m3? 2) A gas increases in volume from 10m3 to 50m3. If the initial pressure was 10,000N/m2 what is the new pressure? 3) A gas decreases in pressure from 100,000 Pascals to 50,000 Pascals. The final volume was 3m3. What was the initial volume? 4) The pressure of a gas changes from 100N/m2 to 20N/m2. What is the ratio for volume change?