* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 9 Systems of Particles - Florida State University
Laplace–Runge–Lenz vector wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Angular momentum operator wikipedia , lookup
Photon polarization wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Brownian motion wikipedia , lookup
Internal energy wikipedia , lookup
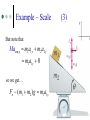
Classical mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Elementary particle wikipedia , lookup
Specific impulse wikipedia , lookup
Equations of motion wikipedia , lookup
Kinetic energy wikipedia , lookup
Seismometer wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Mass in special relativity wikipedia , lookup
Work (physics) wikipedia , lookup
Mass versus weight wikipedia , lookup
Classical central-force problem wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Atomic theory wikipedia , lookup
Center of mass wikipedia , lookup
9. Systems of Particles Center of Mass Center of Mass mi ai Fi i i Consider a system of interacting particles. For each particle, the forces that act on it can be split into internal and external ones. Fi Fi ,int Fi ,ext Internal force External force 3 Center of Mass Fi Fi,int Fi,ext i i i Fi ,ext Fnet ext i Internal force The internal forces sum to zero. Why? The net force on the system of particles is the sum of the external forces only. External force 4 Center of Mass From Fnet ext mi ai i d 2r d 2 mi 2 2 dt dt i m r i i This suggests the definition of center of mass Internal force m r M r i i cm i 5 Center of Mass where m i M is the total mass of the system. i from Fnet ext 2 2 d rcm d 2 mi r M dt i dt 2 we arrive at the 2nd law for the motion of the center of mass. Fnet ext Macm 6 Finding the Center of Mass Example – A Space Station What is the center of mass of a space station, made of three modules of mass m, m and 2m? mx1 mx3 m( x1 x1 ) xcm 0 4m 4m my1 my3 2my1 1 ycm y1 4m 4m 2 3 L 0.43L 4 8 Example – A Skier’s Motion The different parts of the skier’s body follow complex trajectories. But, the center of mass follows a simple parabolic motion. In general, the center of mass moves as if it were a simple particle. 9 Continuous Mass Distributions Consider splitting an object into lots of small pieces of mass Δmi. By definition, the center of mass is given rcm m r i i i M If we make the pieces smaller and smaller we get rcm lim mi 0 m r i i i M r dm M 10 Example – An Aircraft Wing Consider an aircraft wing shaped like an isosceles triangle. Where is its center of mass? Consider the mass of a strip of width dx dm (w/L)x dx 2x dx 1 2 M L 2 wL xcm 1 1 x dm M M 2Mx x 0 L2 dx L 2 L 2 2 x3 L 2 L3 2 2 x dx 2 2 L L 0 L 3 0 3L 3 11 Example – Scale (1) What does the scale read as the block slides down the wedge? We need to compute the normal force, Fn This looks very complicated! But, we know that the motion of the center of mass is often simple. So, let’s try to solve the problem that way. 12 Example – Scale (2) Consider motion in the vertical direction: F i ,ext,y Macm,y i and taking up to be +ve, we have Fn m1 g m2 g Macm,y 13 Example – Scale (3) But note that Macm,y m1a1 y m2 a2 y m1a1 y 0 so we get… Fn (m1 m2 ) g m1a1 y 14 Example – Scale (4) The magnitude of the acceleration down the slope is a g sin therefore, the vertical acceleration of block 1 is a1 y g sin 2 15 Example – Scale (5) So, finally, we deduce that the scale reads: Fn (m1 m2 m1 sin ) g 2 16 Conservation of Momentum Conservation of Momentum Start with Newton’s 2nd Law and assume that the external forces sum to zero dvi i mi dt i Fi,ext 0 Integrate both sides p i i constant where p mv is the momentum 18 Conservation of Momentum If the net external force on a system of particles is zero, the total momentum of the system is constant, that is, conserved. p i constant i 19 Kinetic Energy of a System Kinetic Energy of a System 2 1 Consider the total kinetic energy K 2 mi vi i of a system of particles. This can be rewritten as K = Kcm + Kint, where the first term is the kinetic energy of the center of mass and the second is the kinetic energy relative to the center of mass. 21 Collisions Momentum in Collisions Start with the 2nd Law Then integrate over a short period from ti to tf dp F ma dt tf ti Fdt tf ti dp dt dt tf dp p f pi p ti 23 Momentum in Collisions The integral of a force over a short period from ti to tf is called the impulse tf I Fdt ti p Average force I Fav t 24 Example – Impulse (1) A car drives into a wall at 25 m/s (about 56 mph). What’s the average force of the seatbelt on a crash dummy of mass 80 kg? I p Fav t t 25 Example – Impulse (2) Impulse p mv f mvi 0 mvi 2000 N s iˆ Estimate collision time, and use average speed of 12.5 m/s x 1m t 0.08s vav 12.5 m/s Force Fav 25,000 N iˆ 26 Totally Inelastic Collisions Perfectly Inelastic Collisions: particles stick together Before m1 m2 m1 m2 After Since the net external force is zero, momentum is conserved m1v1i m2 v2i (m1 m2 )v f 27 Totally Inelastic Collisions However, although momentum is conserved, it turns out that kinetic energy is not! Before m1 m2 m1 m2 After Where does the energy go? 28 Example The Ballistic Pendulum This is a device to measure the speeds of fast-moving objects, like bullets. The bullet gets lodged in the wooden block and causes the block to move upwards a height h. Let’s break the problem into two parts: 1. An inelastic collision between bullet and block 2. The rise of the block v m h M 29 Example The Ballistic Pendulum Inelastic collision: Since the net external force is zero, momentum is conserved: mv (m M )V V is the velocity of the bullet plus block. But, note, kinetic energy is not: K i 12 mv 2 K f (m M )V 1 2 m mM Ki 2 v m h M 30 Example The Ballistic Pendulum The rise: In moving up by an amount h, momentum is no longer conserved. Why? But mechanical energy is. The final energy = initial energy 1 (m M )V 2 (m M ) gh 2 therefore, mM v 2 gh m v m h M 31 Elastic Collisions Elastic Collisions Momentum before m1v1i m2v2i m1 m2 m1 m2 Momentum after m1v1 f m2 v2 f 33 Elastic Collisions Momentum after m1 = m2 Momentum before m1 m2 m1v1 f m2 v2 f m1v1i m2 v2i We have 2 unknowns → therefore, need 2 equations 34 Perfectly Elastic Collisions Perfectly Elastic Collisions: Kinetic energy after = kinetic energy before m1 1 2 m1 m2 mv m v 2 1 1f 1 2 2 2 2f m2 mv m v 1 2 2 1 1i 1 2 2 2 2i 35 Perfectly Elastic Collisions m1 m1 m2 m2 m1v1 f m2 v2 f m1v1i m2 v2i We have 2 unknowns and we now have 2 equations 1 2 mv m v 2 1 1f 1 2 2 2 2f mv m v 1 2 2 1 1i 1 2 2 2 2i 36 Perfectly Elastic Collisions m1 m2 m1 m2 From the two equations, we can derive the following: v1 f v2 f (v1i v2i ) This shows that the final relative velocity between the particles is the reverse of the initial relative velocity, but has the same magnitude. 37 Summary The center of mass of a system of particles is defined by rcm (1/ M ) mi ri i The center of mass satisfies Fnet = Macm, where M is the total mass and acm is the acceleration. If the net external force is zero, momentum is conserved. Kinetic energy is conserved only in perfectly elastic collisions. 38