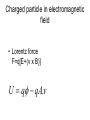Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Classical Mechanics 420
Document related concepts
Four-vector wikipedia , lookup
Canonical quantization wikipedia , lookup
Brownian motion wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
First class constraint wikipedia , lookup
Hunting oscillation wikipedia , lookup
N-body problem wikipedia , lookup
Photon polarization wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Dirac bracket wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Matter wave wikipedia , lookup
Virtual work wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Joseph-Louis Lagrange wikipedia , lookup
Seismometer wikipedia , lookup
Classical mechanics wikipedia , lookup
Electromagnetism wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Analytical mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Transcript
Classical Mechanics 420 J. D. Gunton Lewis Lab 418 [email protected] D’Alembert’s Principle and Lagrange Equations • Use principle of virtual work to derive • Lagrange equations for systems with holonomic constraints Don’t ever give up! Physics Student PhD Program Homework Set 1 Number 2 Double Pendulum: General Coordinates Constrained motion Bead slides without friction on a vertical circular loop, in a uniform Gravitational field. Hoop rotates at a constant angular velocity. Vertical Disk Rolling On Plane Velocity dependent potentials: if forces derived from U via Charged particle in electromagnetic field • Lorentz force F=q[E+(v x B)] U q qA.v Polar Coordinates Atwood’s Machine V= -M1g x – M2 g(l-x) Bead sliding on rotating straight wire, g=0 Constrained motion Bead slides without friction on a vertical circular loop, in a uniform Gravitational field. Hoop rotates at a constant angular velocity. Problem to think about
