Download File

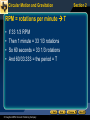
Circular Motion and Gravitation
Section 1
What do you think?
• Consider the following objects moving in circles
at constant speeds`:
•
•
•
•
A ball tied to a string being swung in a circle
The moon as it travels around Earth
A child riding rapidly on a playground merry-go-round
A car traveling around a circular ramp on the highway
• For each example above, answer the following:
• What is keeping the object in the circular path?
• Are the objects accelerating?
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 1
Ok, what did we learn?
•
•
•
•
An object moving in a circle is accelerating.
So, there must be a force.
The force is always pointed towards the center!
This “center- seeking” force is called a
centripetal force (LEARN THIS!!!)
• The feeling that you are being pulled outward is
your INERTIA and is called centrifugal (center
fleeing) and is a FALSE FORCE!!!
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Tangential Speed (vt)
• Speed in a direction tangent to the
circle - AKA linear speed
• Uniform circular motion: vt has a
constant value
– Only the direction changes
• Angular speed is 2p/T where T is
the period. w = DQ /Dt = 2p/T
• How would the angular speed of a
horse near the center of a carousel
compare to one near the edge?
Tangential? Why?
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Tangential Speed (vt)
• (2pr)/ T
• Tangential speed = the
circumference divided by the
Period (T)
• The Period is the time of one
revolution.
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Centripetal Acceleration (ac)
• Acceleration is a change in
velocity (speed and/or direction).
• Direction of velocity changes
continuously for uniform circular
motion.
• What direction is the acceleration?
– the same direction as Dv
– toward the center of the circle
• Centripetal means “center
seeking”
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Section 1
Centripetal Acceleration (magnitude)
• How do you think the magnitude of the acceleration
depends on the speed?
• How do you think the magnitude of the acceleration
depends on the radius of the circle?
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 1
Tangential Acceleration
• Occurs if the speed CHANGES
• Directed tangent to the circle
• Example: a car traveling in a circle
– Centripetal acceleration maintains the circular motion.
• directed toward center of circle
– Tangential acceleration produces an increase or
decrease in the speed of the car.
• directed tangent to the circle
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Centripetal Acceleration
Click below to watch the Visual Concept.
Visual Concept
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Centripetal Force (Fc)
Fc  mac
vt 2
and ac 
r
mvt 2
so Fc 
r
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Centripetal Force
• Maintains motion in a circle
• Can be produced in different
ways, such as
– Gravity
– A string
– Friction
• Which way will an object
move if the centripetal force
is removed?
– In a straight line, as shown on
the right
© Houghton Mifflin Harcourt Publishing Company
Section 1
Circular Motion and Gravitation
Section 1
Describing a Rotating System
• Imagine yourself as a passenger in a car turning quickly
to the left, and assume you are free to move without the
constraint of a seat belt.
– How does it “feel” to you during the turn?
– How would you describe the forces acting on you during this
turn?
• There is not a force “away from the center” or “throwing
you toward the door.”
– Sometimes called “centrifugal force”
• Instead, your inertia causes you to continue in a straight
line until the door, which is turning left, hits you.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 1
Classroom Practice Problems
• A 35.0 kg child travels in a circular path with a
radius of 2.50 m as she spins around on a
playground merry-go-round. She makes one
complete revolution every 2.25 s.
– What is her speed or tangential velocity? (Hint: Find
the circumference to get the distance traveled.)
– What is her centripetal acceleration?
– What centripetal force is required?
• `Answers: 6.98 m/s, 19.5 m/s2, 682 N
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
What do you think?
Imagine an object hanging from a spring scale.
The scale measures the force acting on the
object.
• What is the source of this force? What is pulling or
pushing the object downward?
• Could this force be diminished? If so, how?
• Would the force change in any way if the object was
placed in a vacuum?
• Would the force change in any way if Earth stopped
rotating?
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Newton’s Thought Experiment
• What happens if you fire a
cannonball horizontally at
greater and greater speeds?
• Conclusion: If the speed is
just right, the cannonball will
go into orbit like the moon,
because it falls at the same
rate as Earth’s surface
curves.
• Therefore, Earth’s
gravitational pull extends to
the moon.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Law of Universal Gravitation
• Fg is proportional to the product of the masses (m1m2).
• Fg is inversely proportional to the distance squared (r2).
– Distance is measured center to center.
• G converts units on the right (kg2/m2) into force units (N).
– G = 6.673 x 10-11 N•m2/kg2
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Law of Universal Gravitation
© Houghton Mifflin Harcourt Publishing Company
Section 2
Circular Motion and Gravitation
Section 2
Gravitational Force
• If gravity is universal and exists between all
masses, why isn’t this force easily observed in
everyday life? For example, why don’t we feel a
force pulling us toward large buildings?
– The value for G is so small that, unless at least one of
the masses is very large, the force of gravity is
negligible.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Ocean Tides
•
•
•
•
What causes the tides?
How often do they occur?
Why do they occur at certain times?
Are they at the same time each day?
© Houghton Mifflin Harcourt Publishing Company
Section 2
Circular Motion and Gravitation
Section 2
Ocean Tides
• Newton’s law of universal gravitation is used to explain
the tides.
– Since the water directly below the moon is closer than
Earth as a whole, it accelerates more rapidly toward
the moon than Earth, and the water rises.
– Similarly, Earth accelerates more rapidly toward the
moon than the water on the far side. Earth moves
away from the water, leaving a bulge there as well.
– As Earth rotates, each location on Earth passes
through the two bulges each day.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Gravity is a Field Force
• Earth, or any other mass,
creates a force field.
• Forces are caused by an
interaction between the
field and the mass of the
object in the field.
• The gravitational field (g)
points in the direction of
the force, as shown.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Calculating the value of g
• Since g is the force acting on a 1 kg object, it
has a value of 9.81 N/m (on Earth).
– The same value as ag (9.81 m/s2)
• The value for g (on Earth) can be calculated
as shown below.
Fg
GmmE GmE
g

 2
2
m
mr
r
© Houghton Mifflin Harcourt Publishing Company
Section 2
Circular Motion and Gravitation
Section 2
Classroom Practice Problems
• Find the gravitational force that Earth
(mE = 5.97  1024 kg) exerts on the moon
(mm= 7.35  1022 kg) when the distance between
them is 3.84 x 108 m.
– Answer: 1.99 x 1020 N
• Find the strength of the gravitational field at a
point 3.84 x 108 m from the center of Earth.
– Answer: 0.00270 N/m or 0.00270 m/s2
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
RPM = rotations per minute  T
•
•
•
•
If 33 1/3 RPM
Then 1 minute = 33 1/3 rotations
So 60 seconds = 33 1/3 rotations
And 60/33.333 = the period = T
© Houghton Mifflin Harcourt Publishing Company
Section 2
Circular Motion and Gravitation
Section 2
What do you think?
• Electric forces and gravitational forces are both
field forces. Two charged particles would feel the
effects of both fields. Imagine two electrons
attracting each other due to the gravitational
force and repelling each other due to the
electrostatic force.
• Which force is greater?
• Is one slightly greater or much greater than the other, or are
they about the same?
• What evidence exists to support your answer?
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Coulomb’s Law
• The force between two charged particles depends on the
amount of charge and on the distance between them.
– Force has a direct relationship with both charges.
– Force has an inverse square relationship with distance.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Coulomb’s Law
• Use the known units for q, r, and F to determine the units
of kc.
– kc = 9  109 N•m2/C2
• The distance (r) is measured from center to center for
spherical charge distributions.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 2
Classroom Practice Problem
• The electron and proton in a hydrogen atom are
separated, on the average, a distance of about
5.3  10-11 m. Find the magnitude of both the
gravitational force and the electric force acting
between them.
– Answer: Fe = 8.2  10-8 N, Fg = 3.6  10-47 N
• The electric force is more than 1039 times
greater than the gravitational force.
– Atoms and molecules are held together by electric
forces. Gravity has little effect.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Compare and contrast
© Houghton Mifflin Harcourt Publishing Company
Section 2
Circular Motion and Gravitation
Section 2
Classroom Practice Problem
• A balloon is rubbed against a small piece of
wool and receives a charge of -0.60 C while the
wool receives an equal positive charge. Assume
the charges are located at a single point on each
object and they are 3.0 cm apart. What is the
force between the balloon and wool?
• Answer: 3.6 N attractive
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 4
Torque
• Where should the cat push on
the cat-flap door in order to
open it most easily?
– The bottom, as far away from the
hinges as possible
• Torque depends on the force
(F) and the length of the lever
arm (d).
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 4
Torque
• Torque also depends on the angle between the force (F)
and the distance (d).
• Which situation shown above will produce the most
torque on the cat-flap door? Why?
– Figure (a), because the force is perpendicular to the distance
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Section 4
Torque
• SI units: N•m
– Not joules because torque is not
energy
• The quantity “d ” is the
perpendicular distance from the
axis to the direction of the force.
© Houghton Mifflin Harcourt Publishing Company
Circular Motion and Gravitation
Torque as a Vector
• Torque has direction.
– Torque is positive if it causes a
counterclockwise rotation.
– Torque is negative if it causes a
clockwise rotation.
• Are the torques shown to the
right positive or negative?
– The wrench produces a positive
torque.
– The cat produces a negative
torque.
• Net torque is the sum of the
torques.
© Houghton Mifflin Harcourt Publishing Company
Section 4
Circular Motion and Gravitation
Classroom Practice Problems
• Suppose the force on the wrench is
65.0 N and the lever arm is 20.0 cm.
Calculate the torque.
• If that was not enough torque to do
the job, what could you do?
• Using a cheat pipe, you increase the
lever arm to 60.0 cm. What is the
torque now?
© Houghton Mifflin Harcourt Publishing Company
Section 4