Download Rotational Motion

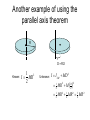
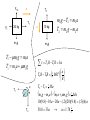
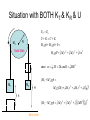
Rotational Motion
AP Physics
Lyzinski, CRHS-South
Day
#1
Sections 10.1 & 10.2
Polar coordinates (r, )
P
r
CCW is positive, CW is negative
s = arc length =

s
C
r
Where does it come from?

360
o

s
circumference


2 (rad )

s
2R

s  R
 = angular position (measured in radians, not degrees)
 = Angular displacement  2  1
Degree to radian conversion
 (rad ) 

180
 (deg)
w = Angular velocity

avg angular velocity = w 
Instantaneous angular velocity = w  lim
t 

t
 d

t
dt
Units of radians per second (rad/s)
a = Angular acceleration
 avg angular acceleration = a 
w dw d 2

 2
Instantaneous angular acceleration = a  lim
t   t
dt
dt
Units of radians per second squared (rad/s2)
w
t
Translational vs. Rotational Motion
v
dx
dt
dv d 2 x
a
 2
dt dt
v2  v1  at
d
dt
dw d 2
a
 2
dt
dt
w
w2  w1  at
v 2  v1  2ax
w2 2  w12  2a
x  12 at 2  v1t
  12 at 2  w1t
x  12 t (v1  v2 )
  12 t (w1  w2 )
2
2
CAUTION!!! These equations can only be used if a or a are constant!!!!!
In-Class Example Problem
#6
A rotating wheel requires 3.00 s to rotate through 37.0 revolutions.
Its angular speed at the end of the 3.00-s interval is 98 rad/s.
What is the constant angular acceleration of the wheel?
t  3 sec
w2  98
rad
s
37 rev  2 rad 

  232.478 rad
  37 rev 
1  1 rev 
a  ???
  12 t (w1  w2 )
w2  w1  at


232.478  12 (3)(w1  98)
98  56.985  3a

w1  56.985 rad
s

a  13.67 rad
s
2
Class Practice
• A rotating wheel requires 3.00 s to rotate
through 37.0 revolutions. Its angular
speed at the end of the 3.00-s interval is
98 rad/s. What is the constant angular
acceleration of the wheel?
In-Class Example Problem
#9 The tub of a washing machine goes into its spin cycle, starting from
rest and gaining angular speed steadily for 8.00 s, at which time it is
turning at 5.00 rev/s. At this point, the person doing the laundry
opens the lid and a safety switch turns off the machine. The tub
smoothly slows to rest in 12.0 s. Through how many revolutions
does the tub turn while its in motion?
t  8 sec
w1  0 w2  5 revs
  12 t (w1  w2 )  12 (8)(0  5)  20 rev
w1  5 revs
w2  0
t  12 sec
  12 t (w1  w2 )  12 (12)(5  0)  30 rev
50 revs total
In-Class Example Problem
A Mr. L original 
A certain wheel begins to rotate. Its position varies with time according
to the equation
  3t 2  6t  5 rad
Find the wheel’s average angular acceleration between 5 and 9 sec.
a
w
t
d
 w  6t  6  rad
s
dt
w (5)  6(5)  6  36 rad
s
Duh!!! The
acceleration is
constant 
w (9)  6(9)  6  60 rad
s
rad
24 rad
w
w (9)  w (5) 60 rad
s  36 s
s
a



 6 rad
s
t
9  5 sec
9  5 sec
4 sec
2
Day #1 HW Assignment
pp. 299-300
Do problems 1-7 all (skip # 6 and #7b)
Day
#2
Section 10.3
v
w
r

Relating Rotational Motion (, w, and a)
to Translational Motion (x, v, and a)
s
ds d (r )
d
v

r
 rw
dt
dt
dt
dv d (rw )
dw
at 

r
 ra
dt
dt
dt
Point of rotation
Note: As r increases, v and a
get larger, while w and a
stay the same.
v 2 (rw ) 2
ar  
 rw 2
r
r
a  at  ar  (ra ) 2  (rw 2 ) 2  r a 2  w 4
2
2
In-Class Example Problem
#16
A car accelerates uniformly from rest and reaches a speed of 22.0
m/s in 9.00 s. The tires have diameter 58.0 cm and do not slip on
the pavement. (a) Find the number of revolutions each tire makes
during this motion. (b) What is the final angular speed of a tire in
revolutions per second?
v1  0
a  aR
v2  22 ms

t  9 sec

v2  v1  at

a  2.4 sm2
a 2.4 ms
a 
 8.429 rad
s2
R .29m
2
  12 at 2  w1t  12 (8.429 rad
2 )(9)  0  341.37 rad  54.33 rev
s
rad
rev
w2  w1  at  0  (8.429 rad
)(
9
)

75
.
9

12
.
1
s
s
s
2
In-Class Example Problem
#12
The drive train of a bicycle is shown. The wheels have a diameter
of 67.3 cm and the pedal cranks are 17.5 cm long. The cyclist
pedals at a steady cadence of 76.0 rev/min. The chain engages
with a front sprocket 15.2 cm in diameter and a rear sprocket 7.00
cm in diameter. (a) Calculate the speed of a link in the chain
relative to the bicycle frame. (b) Calculate the angular speed of
the bicycle wheels. (c) Calculate the speed of the bicycle relative
to the road.
rev
w pedals  76 min
 7.959 rad
s
rwheel  .3365m
rfront sprocket  .152m
rrear sprocket  .07m
m

vchain  w pedalsrfront sprocket  7.959 rad
(.
076
m
)

.
604
s
s
vchain  wwheel rrear sprocket

.604  ww (.035)
vwheels  wwheel rwheel  (17.257)(.3365)  5.8 ms

ww  17.257 rad
s
Day #2 HW Assignment
pp. 300-301
Do problems 10, 13, 14, 15, 16, 19
Day
#3
Section 10.4
Rotational Energy
A solid object is a collection of particles. When the object
rotates, each of these particles moves, thus possessing
kinetic energy. If we add up all these individual energies, we
can find the energy associated with the rotating object.
However, as we have learned previously, the velocity of each
particle depends on how far the particle is from the axis of
rotation. Particles close the axis move slower than particles
far from the axis (according to v = rw). Therefore, it might be
useful to express each individual kinetic energy in terms of w
(which is the same for each particle) instead of v (which
changes based on distance from the axis).
K R  Rotational Kinetic Energy   K i
i
  mi vi  
2
1
2
i
i
1
2

2 2
mi (riwi )    mi ri w
 i

2
KE of each
individual
particle
The term
m r
i i
1
2
Notice that w was taken out of the
summation because it is the same for
every particle, no matter how far the
particle is from the axis of rotation.
2
has been given the name “the Moment of Inertia”, or “I” .
i
Therefore,
K R  Iw
1
2
2
“I” has units of
kg  m
2
What is “Inertia”?
Remember, in translational motion, an object’s inertia is its
“tendency” to want to either remain at rest or moving at a
constant velocity. An object’s mass is a direct measure of its
inertia.
In rotational motion, the individual particles have masses at
different distances from the axis of rotation. The Moment of
inertia is the rotational analog of mass. It is a measure of how
difficult it is to change an object’s motion about its axis of
rotation. The closer the mass is to the axis, the easier it is to
change its rotational motion. Thus, objects with more of their
mass far from the axis rotation have a higher moment of
inertia.
Translational vs. Rotational Motion (revised)
dv d 2 x
a
 2
dt dt
dx
v
dt
d
w
dt
dw d 2
a
 2
dt
dt
v2  v1  at
w2  w1  at
v 2  v1  2ax
w2 2  w12  2a
x  12 at 2  v1t
  12 at 2  w1t
x  12 t (v1  v2 )
  12 t (w1  w2 )
2
2
K  mv
1
2
2
K R  12 Iw 2
In-Class Example Problem
A Mr. L original 
A Penn State Baton Twirler is spinning her 2 ft long baton, which has
identical end masses of 300 grams. Assuming the rod itself to be
mass-less, find the moment of inertia of the baton if she rotates it
about (a) line “a” (which is through the center of the rod) or (b) line
“b” (which is 4 inches off-center).
1 ft  .3048 m
16 in  .4064 m
8 in  .2032 m
I a   mi ri  (.300kg)(. 3048m) 2
2
 (.300kg)(. 3048m) 2  .0557 kg  m 2
I a   mi ri  (.300kg)(. 4064m) 2
2
a
b
 (.300kg)(. 2032m) 2  .0619 kg  m 2
In-Class Example Problem
#25
2.86 m
0.12 kg
Before
60.0 kg
14.0 cm
v
Find the speed that the small mass
leaves the Trebuchet. Assume the rod
to be mass-less.
I   mi ri  (.12)( 2.86) 2  (60)(.14) 2  2.158 kg  m 2
2
Eb  Ea
mgh  Mgh  12 Iw 2  mgH
(.12)(9.8)(.14)  (60)(9.8)(. 14)
 12 (2.158)w 2  (.12)(9.8)(3)
After
w  8.55 rad
s
v  wr  (8.55)( 2.86)  24.5 ms
Day #3 HW Assignment
pp. 301-302
Do problems 21, 22, 23
Day
#4
Section 10.5
Calculating
Moments of Inertia
I
Notice that the object
with more of its mass
further away from the
axis of rotation has a
larger moment of inertia
(and thus it will be
harder to change it
rotational motion)
1
MR 2
2
I  MR 2
I   mi ri  lim
2
I  MR 2
I
2
mi 0
i
1
MR 2
2
I
I
2
r

m

r
 i i  dm
i
2
MR 2
5
2
MR 2
3
I
I
1
MR 2
12
1
MR 2
3
Calculating
Moments of Inertia
I
1
MR 2
2
I  MR 2
I  MR 2
I
1
MR 2
2
I
I
I   mi ri  lim
2
mi 0
i
2
MR 2
5
2
MR 2
3
I
I
1
MR 2
12
1
MR 2
3
2
r

m

r
 i i  dm
2
i
Again, notice that
the object with
more of its mass
further away from
the axis of rotation
has a larger
moment of inertia
Using Calculus to find Moments of Inertia
• First, make sure to figure out what your “tiny
pieces” look like.
• Second, choose the appropriate density
function for your “tiny piece” (l for linear, s for
area, or r for volume).
• Third, use the appropriate density function and
solve for dm.
• Fourth, make sure that dm only has one
variable in it, and then plug it into
2
I   r dm
L
y
x
dm with
thickness dL
Example: Find the moment of inertia of a
thin rod that rotates about its end.
m
l
L
lL  m


L
L
L
0
0
0
ldL  dm

ldx  dm
I   r 2 dm   r 2 (ldx)   x 2 (ldx)
 l  x dx  l  x
L
2
0
1
3

3 L
0
m 3
 L
3
lL  L 
mL3 1 2



 mL
3
3
3L 3
y
Example: Find the moment of inertia of a
dm with
thickness dr
R
solid cylinder that rotates about its
central axis.
r
r
r
m
V
rV  m


rdV  dm


zero, b/c tiny times tiny
equals super tiny

dV   (r  dr ) 2  r 2 
L  2rdr   (dr ) 2
 height

area of ring
dr
 dm  r (2Lrdr )
r
Top view of the “thin”
cylindrical slices
L
L
R
 
I   r dm   r 2rLrdr  2rL  r 3 dr 2rL 14 r 4
2
2
0
0

R
0
0





m
 m 
 2rL 14 R 4  2   L 14 R 4  2  2  L 14 R 4  12 MR 2
V 
 R L 
Example: Find the moment of inertia of a
dm with
thickness dr
sphere about its central axis.
R
m

rV  m
V
dV  43  (r  dr ) 3  43 r 3
r

Volume of outer
sphere

rdV  dm

Volume of
inner sphere
(r  dr ) 3  r 3  r 2 dr  r (dr ) 2  r 2 dr  r (dr ) 2  (dr ) 3
 dm  43 r(r 2 dr  r ( dr ) 2  r 2 dr  r (dr ) 2  (dr ) 3 )
zero, b/c tiny
times tiny equals
super tiny
 43 r(2r 2 dr )
R
R
I   r dm   r
2
0
r(2r dr )  83 r r 4 dr  83 r15 r 5 0
R
2 4
3
R
2
0
0
 m 
m
 83 r 15 R 5  83    15 R 5  83   4 3  15 R 5  52 mR 2
V 
 3 R 






Using the parallel axis theorem to
calculate moments of inertia
If you know the moment of inertia of an object about a given axis, you can
use the equation
2
I  I CM  MD
to find the moment of inertia of this object about any axis parallel to the given
axis. The distance between these axis is “D”.
Known:
1
I  ML2
12
D
Unknown:
I  I CM  MD 2

1
12
ML  M 
2

L 2
2
 121 ML2  14 ML2  13 ML2
Another example of using the
parallel axis theorem
R
D = R/2
Known:
1
I  MR 2
2
Unknown:
I  I CM  MD 2
 12 MR 2  M  R2 
2
 12 MR 2  14 MR 2  34 MR 2
Sections 10.6 & 10.7
Torque (t): The tendency of a force to rotate
an object about a given axis.
F
F sin

r
F cos
d
t  rF sin   Fd
“d” is known as the “moment
arm” or “lever arm”
***Notice that only forces perpendicular
to the lever arm cause a torque
Some notes about TORQUE
•
The units of torque (t) are N-m
•
The direction of a torque is found using the Right-Hand-Rule
– Place your fingers in the direction of the lever arm.
– “Slap” in the direction of the force.
– Your thumb points in the direction of the torque.
– The direction of a torque is found using the Right-Hand-Rule
•
Positive torques are CCW and negative torques are CW.
•
Torque is NOT a force!!!
•
Torque is NOT the same as work. They have the same units, but are VERY
different.
•
The net torque on an object is the vector sum of the individual torques.
Therefore,
t  t i
How are torques and forces different?
• Forces can cause a change in motion in
translational motion.
• Forces can cause a change motion in rotational
motion. HOWEVER, the further the force is from
the axis of rotation, the more “effective” it will be
in changing motion. Thus, the force as well as
the length of the “lever arm” are important in
rotational motion. Therefore, instead of
speaking only of a “force”, we speak of a
“torque”.
Newton’s 2nd Law (for a particle)
 Ft  mat
 F  m(ra )
 F r  m(ra )r
t  mr a
t  Ia
The net force on a particle is proportional
to its TANGENTIAL acceleration.
t
t
2
The net torque on a particle is proportional
to its ANGULAR acceleration.
Newton’s 2nd Law (for a rigid body)
Ft  mat
Ft  m(ra )
Ft r  m(ra )r
t  mr 2a
 
 dt   r a dm
Every “tiny little” mass (dm) in the rigid body is
located at a different distance from the axis of
rotation, and this needs to be taken into account.
Also, each of these masses is subjected to its
own individual “tiny little” torque (dt). To get the
total torque, we need to sum up ALL of the “tiny
little” ones (by integrating).
dt  r 2a dm
2

2
t

a
r

 dm

t  Ia
Mass-less Pulleys
R
R
M=0
T1
T2
t net  Ia
T1 R  T2 R  12 MR 2a
M1
M2
Mass-less pulleys don’t
really exist (but make
calculations easy )
T1 R  T2 R  (0) R a
1
2
T1 R  T2 R  0
T1  T2
2
All a mass-less pulley
does is change the
direction of a force.
Mass-ful Pulleys
R
R
M
T1
T2
t net  Ia
T1 R  T2 R  MR a
1
2
M1
M2
The pulley in this
example is modeled as
a solid disk (and thus
I = ½ MR2)
2
T1 R  12 MR 2a  T2 R
 T1  T2
The difference in the
tensions causes the net
torque which forces the
pulley to rotate
In-Class Example Problem
A Mr. L original 
The system below is at rest when the 10 kg mass is released. The
pulley is not mass-less, but rather has a mass of 6 kg and a radius
of 20 cm. If the surface has a coefficient of friction of 0.2, find the
acceleration of the system.
20 kg
10 kg
FN1
a
T2
T1
Ff
20 kg
m1 g
m2 g  T2  m2 a
a
10 kg
T2  m2 g  m2 a
m2 g
T1  m1 g  m1a
t  T R  T R  Ia
T1  m1a  m1 g
2
T2 R  T1 R 
a
T1
1

1
2

a
MR  
R
2
T2  T1  12 Ma
m2 g  m2 a   m1a  m1 g   12 Ma
10(9.8)  10a  20a  (.2)( 20)(9.8)  (.5)(6)a
T2
58.8  33a

a  1.78 sm2
Translational vs. Rotational Motion (revised)
dv d 2 x
a
 2
dt dt
dx
v
dt
d
w
dt
dw d 2
a
 2
dt
dt
v2  v1  at
w2  w1  at
v 2  v1  2ax
w2 2  w12  2a
x  12 at 2  v1t
  12 at 2  w1t
x  12 t (v1  v2 )
  12 t (w1  w2 )
2
2
K  mv
1
2
2
Fnet  ma
K R  12 Iw 2
t net  Ia
Section 10.8
Work & energy in Rotational Motion
W  t
(similar t o W  Fx)
dW d
d

 t   t
 tw
dt
dt
dt
K R  12 Iw 2
W  K  U
(similar t o   Fv)
(similar t o KT  12 mv2 )
(where K now equals K T  K R )
If no external torques or forces are present, then Eb = Ea.
Situations with ONLY KT
W  K
Fx  12 mv2  12 mv1
2
2
Situations with ONLY KR
Rotating Wheel
(where the axis of
rotation is fixed)
W  K
t  12 Iw2 2  12 Iw12
Situation with BOTH KT & KR
A Rolling Object
(it is rotating and translating
at the same time)
K  I CM w  M CM v
2
1
2
K due to
rotation
1
2
K due to
translation
2
Situation with BOTH KT & KR & U
Eb  Ea
U  K U  K
R
M2
M 1 gh  M 3 gh  0 
M 3 gH  12 M 1v 2  12 M 1v 2  12 Iw 2
Solid Disk
since w  Rv , H  2h, and I  12 MR 2
M3
M1
( M 1  M 3 ) gh 
H
M 3 g (2h)  12 M 1v 2  12 M 1v 2  12 I  Rv 
2
h
( M 1  M 3 ) gh  12 M 1v 2  12 M 1v 2  12
Zero level

1
2
MR 2
 
v 2
R
Situation with BOTH KT & KR & U
Eb  Ea
U  K U  K
R
h
Mgh  0  Mg ( R)  12 Mv 2  12 Iw 2
since w  Rv , and I  MR 2 (for a thin hoop)
Mgh  0  MgR  12 Mv 2  12 MR 2  Rv 
2
Mgh  0  MgR  12 Mv 2  12 MR 2
Find the velocity of the thin hoop
(with radius “R”) at the bottom.
Mgh  MgR  Mv 2

 
v2
R2
v  g (h  R)
Review Day 
Section 10.9
Rolling without slipping
• In order to roll, an object needs to encounter friction, which applies
a torque to the object and causes a rotation about its center of
mass.
• If an object does not slip at all while rolling, it is said to undergo
PURE rolling motion.
• For pure rolling motion,
vCM
aCM
ds d (r )
d


r
 rw
dt
dt
dt
dvCM d (rw )
dw


r
 ra
dt
dt
dt
These conditions
must hold for
non-slip rolling.
A closer look at an object that rolls but doesn’t slip
(part 1)
When an object undergoes PURE rotation, every point on the object has
the same angular velocity, Therefore, all points that are equidistant from
the axis of rotation have the same tangential velocity.
vt = Rw
v=0
vt = Rw
A closer look at an object that rolls but doesn’t slip
(part 2)
When an object undergoes PURE translation (which is the equivalent of
ALL slip and NO roll), every point on the object has the same velocity,
namely the velocity of the center of mass.
vCM
vCM
vCM
A closer look at an object that rolls but doesn’t slip
(part 3)
When an object undergoes PURE Rolling, this is a combination of both
ROTATION and TRANSLATION. While every point on the object has the
same angular velocity, the contact point with the floor acts as a pivot
point. Thus, points on the rotating object that are furthest from the floor
have the largest tangential velocity.
.
vt = vCM+ Rw  2vCM
vCM
v=0
Day #8 HW Assignment
Review for Test
Days 9 thru 11 HW Assignment
Day
12
Test Day !!!!