* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Electrical resistivity and conductivity wikipedia , lookup
History of quantum field theory wikipedia , lookup
Casimir effect wikipedia , lookup
Anti-gravity wikipedia , lookup
Spin (physics) wikipedia , lookup
Field (physics) wikipedia , lookup
Electromagnetism wikipedia , lookup
Superconductivity wikipedia , lookup
Photon polarization wikipedia , lookup
Nuclear structure wikipedia , lookup
Nuclear physics wikipedia , lookup
Metallic bonding wikipedia , lookup
Bent's rule wikipedia , lookup
Molecular orbital wikipedia , lookup
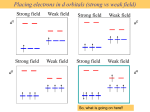
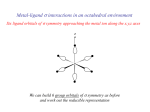
Coordination Chemistry Bonding in transition-metal complexes Crystal field theory: an electrostatic model - + - - The metal ion will be positive and therefore attract the negatively charged ligands But there are electrons in the metal orbitals, which will experience repulsions with the negatively charged ligands Ligand/d orbital interactions Orbitals point at ligands (maximum repulsion) Orbitals point between ligands (less pronounced repulsion) The two effects of the crystal field Splitting of d orbitals in an octahedral field eg 3/5 Do Do 2/5 Do t2g Do is the crystal field splitting E(t2g) = -0.4Do x 3 = -1.2Do E(eg) = +0.6Do x 2 = +1.2Do The magnitude of the splitting (ligand effect) Strong field Weak field The spectrochemical series CO, CN- > phen > NO2- > en > NH3 > NCS- > H2O > F- > RCO2- > OH- > Cl- > Br- > I- The magnitude of the splitting (metal ion effect) Strong field Weak field D increases with increasing formal charge on the metal ion D increases on going down the periodic table The splitting constant must depend on both the ligand and the metal. Do ≈ M ∑ nlLl x 103 Predicts value of D (cm-1) nl is # of ligands Ll Placing electrons in d orbitals Strong field Weak field Strong field Weak field d1 d2 d3 d4 When the 4th electron is assigned it will either go into the higher energy eg orbital at an energy cost of D0 or be paired at an energy cost of P, the pairing energy. d4 Strong field = Low spin (2 unpaired) Weak field = High spin (4 unpaired) P < Do P > Do Notes: the pairing energy, P, is made up of two parts. 1) Coulombic repulsion energy caused by having two electrons in same orbital Pairing Energy, P The pairing energy, P, is made up of two parts. 1) Coulombic repulsion energy caused by having two electrons in same orbital. Destabilizing energy contribution of Pc for each doubly occupied orbital. 2) Exchange stabilizing energy for each pair of electrons having the same spin and same energy. Stabilizing contribution of Pe for each pair having same spin and same energy P = sum of all Pc and Pe interactions Placing electrons in d orbitals d5 1 u.e. 5 u.e. d6 0 u.e. 4 u.e. d8 2 u.e. 2 u.e. d7 1 u.e. 3 u.e. d9 1 u.e. 1 u.e. d10 0 u.e. 0 u.e. Positive favors high spin. Neg favors low spin. Enthalpy of Hydration of hexahydrate Splitting of d orbitals in a tetrahedral field t2 Dt e Dt = 4/9Do Always weak field (high spin) Magnetic properties of metal complexes Diamagnetic complexes very small repulsive interaction with external magnetic field no unpaired electrons Paramagnetic complexes attractive interaction with external magnetic field some unpaired electrons s n(n 2) Measured magnetic moments include contributions from both spin and orbital spin. In the first transition series complexes the orbital contribution is small and usually ignored. Coordination Chemistry: Molecular orbitals for metal complexes The symmetry of metal orbitals in an octahedral environment A1g T1u The symmetry of metal orbitals in an octahedral environment T2g Eg The symmetry of metal orbitals in an octahedral environment s Metal-ligand s interactions in an octahedral environment Six ligand orbitals of s symmetry approaching the metal ion along the x,y,z axes z M We can build 6 group orbitals of s symmetry as before and work out the reducible representation s If you are given G, you know by now how to get the irreducible representations G = A1g + T1u + Eg Now we just match the orbital symmetries s “d0-d10 electrons” anti bonding “metal character” non bonding 6 s ligands x 2e each 12 s bonding e “ligand character” Introducing π-bonding 2 orbitals of π-symmetry on each ligand We can build 12 group orbitals of π-symmetry Gπ = T1g + T2g + T1u + T2u Anti-bonding LUMO(π) The CN- ligand Some schematic diagrams showing how p bonding occurs with a ligand having a d orbital (P), a p* orbital, and a vacant p orbital. ML6 s-only bonding “d0-d10 electrons” anti bonding “metal character” non bonding 6 s ligands x 2e each The bonding orbitals, essentially the ligand lone pairs, 12 s bondingwill e not be worked with further. “ligand character” π-bonding may be introduced as a perturbation of the t2g/eg set: Case 1 (CN-, CO, C2H4) empty π-orbitals on the ligands ML π-bonding (π-back bonding) t2g (π*) t2g eg eg Do D’o Do has increased t2g Stabilization t2g (π) ML6 s-only ML6 s+π (empty π-orbitals on ligands) π-bonding may be introduced as a perturbation of the t2g/eg set. Case 2 (Cl-, F-) filled π-orbitals on the ligands LM π-bonding eg Do has decreased eg D’o t2g (π*) Do Destabilization t2g t2g Stabilization t2g (π) ML6 s-only ML6 s+π (filled π-orbitals) Putting it all on one diagram. Strong field / low spin Weak field / high spin Spectrochemical Series Purely s ligands: D: en > NH3 (order of proton basicity) p donating which decreases splitting and causes high spin: D: H2O > F > RCO2 > OH > Cl > Br > I (also proton basicity) Adding in water, hydroxide and carboxylate D: H2O > F > RCO2 > OH > Cl > Br > I p accepting ligands increase splitting and may be low spin D: CO, CN-, > phenanthroline > NO2- > NCS- Merging to get spectrochemical series CO, CN- > phen > en > NH3 > NCS- > H2O > F- > RCO2- > OH- > Cl- > Br- > I- Strong field, p acceptors large D low spin s only Weak field, p donors small D high spin Turning to Square Planar Complexes z y x Most convenient to use a local coordinate system on each ligand with y pointing in towards the metal. py to be used for s bonding. z being perpendicular to the molecular plane. pz to be used for p bonding perpendicular to the plane, p^. x lying in the molecular plane. px to be used for p bonding in the molecular plane, p|. ML4 square planar complexes ligand group orbitals and matching metal orbitals ML4 square planar complexes MO diagram s-only bonding - bonding A crystal-field aproach: from octahedral to tetrahedral L L L M L L M L L L L L Less repulsions along the axes where ligands are missing A crystal-field aproach: from octahedral to tetrahedral A correction to preserve center of gravity The Jahn-Teller effect Jahn-Teller theorem: “there cannot be unequal occupation of orbitals with identical energy” Molecules will distort to eliminate the degeneracy Angular Overlap Method An attempt to systematize the interactions for all geometries. 1 1 4 M 7 8 3 11 M M 2 9 5 6 2 12 10 6 The various complexes may be fashioned out of the ligands above Linear: 1,6 Tetrahedral: 7,8,9,10 Trigonal: 2,11,12 Square planar: 2,3,4,5 T-shape: 1,3,5 Trigonal bipyramid: 1,2,6,11,12 Square pyramid: 1,2,3,4,5 Octahedral: 1,2,3,4,5,6 Cont’d All s interactions with the ligands are stabilizing to the ligands and destabilizing to the d orbitals. The interaction of a ligand with a d orbital depends on their orientation with respect to each other, estimated by their overlap which can be calculated. The total destabilization of a d orbital comes from all the interactions with the set of ligands. For any particular complex geometry we can obtain the overlaps of a particular d orbital with all the various ligands and thus the destabilization. ligand dz2 dx2-y2 dxy dxz dyz 1 1 es 0 0 0 0 2 ¼ ¾ 0 0 0 3 ¼ ¾ 0 0 0 4 ¼ ¾ 0 0 0 5 ¼ ¾ 0 0 0 6 1 0 0 0 0 7 0 0 1/3 1/3 1/3 8 0 0 1/3 1/3 1/3 9 0 0 1/3 1/3 1/3 10 0 0 1/3 1/3 1/3 11 ¼ 3/16 9/16 0 0 12 1/4 3/16 9/16 0 0 Thus, for example a dx2-y2 orbital is destabilized by (3/4 +6/16) es = 18/16 es in a trigonal bipyramid complex due to s interaction. The dxy, equivalent by symmetry, is destabilized by the same amount. The dz2 is destabililzed by 11/4 es.