* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Module 2 Integer Data
Survey
Document related concepts
Transcript
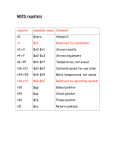
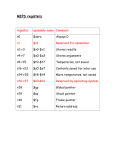
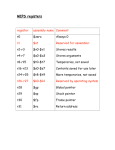
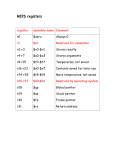
Module 2: Data Representation in Computer Systems B O O K : C O M P U T E R O R G A N I Z AT I O N A N D D E S I G N , 3 E D , D AV I D L . P AT T E R S O N A N D J O H N L . H A N N E S S Y, M O R G A N K A U F M A N N PUBLISHERS Sem11415_hkm Objectives Understand the fundamentals of numerical data representation and manipulation in digital computers. Master the skill of converting between various radix systems. Understand how errors can occur in computations because of overflow and truncation. Understand the fundamental concepts of floating- point representation. Sem11415_hkm Contents Introduction Fixed-Number Representation Unsigned Numbers Signed Numbers Fixed-Number Arithmetic Addition and Subtraction Multiplication Division Floating-Point Representation IEEE-754 Floating-Point Standard Floating-Point Arithmetic Addition Multiplication Sem11415_hkm Introduction Numbers are represented by binary digits (bits): How are negative numbers represented? What is the largest number that can be represented in a computer world? What happens if an operation creates a number bigger than can be represented? What about fractions and real numbers? A mystery: How does hardware really multiply or divide numbers? Sem11415_hkm Arithmetic Operations 5 Complement Addition Subtraction Multiplication Division Sem11415_hkm Fixed-Number Representation Sem11415_hkm Number Numbers are kept in computer hardware as a series of high and low electronic signals. They are considered base 2 numbers (Binary) All information is composed of binary digits or bits. In any number base, the value of ith digit d is d ´ Base i where i start at 0 and increases from right to left Sem11415_hkm Binary Numbers Binary Number System System Digits: 0 and 1 Bit (short for binary digit): A single binary digit LSB (least significant bit): The rightmost bit MSB (most significant bit): The leftmost bit Upper Byte (or nybble): The right-hand byte (or nybble) of a pair Lower Byte (or nybble): The left-hand byte (or nybble) of a pair Sem11415_hkm Binary Numbers 8 bits long Range of numbers that can be represented = = 0 to (28 – 1) = 0 to 255 32 bits long Range of numbers that can be represented = = 0 to (232 – 1) = 0 to 4,294,967,295 Sem11415_hkm Binary Numbers Binary Equivalents 1 Nybble (or nibble) = 4 bits 1 Byte = 2 nybbles = 8 bits 1 Kilobyte (KB) = 1024 bytes 1 Megabyte (MB) = 1024 kilobytes = 1,048,576 bytes 1 Gigabyte (GB) = 1024 megabytes = 1,073,741,824 bytes Sem11415_hkm Recap Sem11415_hkm Numbers: overview Integer Unsigned Numbers Whole DivisionRemainder Signed Fraction Successive Subtraction Multiplication SignedMagnitude Complement One’s Complement Two’s Complement Sem11415_hkm Unsigned Numbers • For positive number only. • Range number = 0 to 2n-1 • There is no negative values representation since number cannot be both. If 32 bits long. Range of numbers that can be represented = 0 to (232 – 1) = 0 to 4,294,967,295 Sem11415_hkm Signed Numbers • • • • • • • • • Integers as binary values can be positive or negative. Problem: How to represent and encode the actual sign of a number? Solution: Need code to represent the signs. Three signed representations covered: Signed Magnitude Ones Complement Twos Complement Sem11415_hkm Signed Numbers: a) Signed Magnitude To represent negative values, computer systems allocate the high-order bit to indicate the sign of a value. The high-order bit is the leftmost bit in a byte. It is also called the Most Significant Bit (MSB). The remaining bits contain the value of the number. If MSB = 0 number is +ve; If MSB = 1 number is -ve Note that this leads to having two representations for the number zero. With an 8-bit number representation: Largest number is +127, smallest number is -127 In 8 bits numbers: Example: +2510= 0001 10012 -2510 = 1001 10012 0000 0000 = +0 0111 1111 = +127 1000 0000 = -0 1111 1111 = -127 Sem11415_hkm Signed Numbers: b) One’s Complement The MSB is the sign bit Negative numbers are obtained by flipping (or complementing) the bit 0 to 1; 1 to 0 Note that this leads to having two representations for the number zero With an 8-bit number representation: Largest number is +127, smallest number is -127 Example: +2510= 0001 10012 -2510 = 1110 01102 In 8 bits numbers: 0000 0000 = +0 0111 1111 = +127 1111 1111 = -0 1000 0000 = -127 Sem11415_hkm Signed Numbers: c) Two’s Complement The MSB is the sign bit Negative numbers are obtained by adding 1 to Ones complement negative. Note that this has only one representation for the number zero With an 8-bit number representation: Largest number is +127, smallest number is -128. Example: +2510= 0001 10012 -2510 = 1110 01112 In 8 bits numbers: 0000 0000 = +0 0111 1111 = +127 1111 1111 = -1 1000 0000 = -128 Sem11415_hkm Calculation of 2's Complement Step 1: invert the binary equivalent of the number by changing all of the ones to zeroes and all of the zeroes to ones (also called 1's complement) 17 = 00010001 Step 2: Then add one. Step1 : 11101110 Example: -17 -17 = 11101111 Step2 : 11101110 + 1 ----------------------11101111 Sem11415_hkm Example: Signed Arithmetic Operation The operation: (-19) + 13 = -6 Signed Magnitude: 10010011 + 00001101 ----------------------10100000 (-32) Ones Complement: 11101100 + 00001101 ----------------------11111001 (-6) Twos Complement: 11101101 + 00001101 ----------------------11111010 (-6) Sem11415_hkm Fixed-Number Arithmetic Sem11415_hkm Binary Numbers Base 2 Sem11415_hkm Binary Addition Rules of Binary Addition 0+0=0 0+1=1 1+0=1 1 + 1 = 0, and carry 1 to the next more significant bit Example: 26 +12 Carry Sem11415_hkm Binary Addition: Example Sem11415_hkm Binary Subtraction (a) Rules of Binary Subtraction 0-0=0 0 - 1 = 1, and borrow 1 from the next more significant bit 1-0=1 1-1=0 borrowed Example: 37 -17 Sem11415_hkm Binary Subtraction (b) Another method : Using addition with 2’s complement Example: 37 -17 37 + (-17) ignore Sem11415_hkm Binary Subtraction (b) Example : 7 – 12 7 + (-12) 7 = 00000111 -12 = 11110100 00000111 + 11110100 ----------------------11111011 (-5) CHECK! -5 = 11111011 Step1 : 00000100 Step2 : 00000100 + 1 ----------------------00000101 (5) Sem11415_hkm Binary Subtraction: Example 27 Sem11415_hkm Sign Extension Extending a number representation to a larger number of bits. Example: 2 in 8 bit binary to 16 bit binary. 00000010 00000000 00000010 In signed numbers, it is important to extend the sign bit to preserve the number (+ve or –ve) Example: -2 in 8 bit binary to 16 bit binary. 11111110 Sign bit 11111111 11111110 Sign bit extended Sign bit Sem11415_hkm Detecting Overflow in Two’s Complement Numbers Overflow occurs when adding two positive numbers and the sum is negative, or vice versa A carry out occurred into the sign bit Overflow conditions for addition and subtraction Sem11415_hkm Overflow Rule for addition If 2 Two's Complement numbers are added, and they both have the same sign (both positive or both negative), then overflow occurs if and only if the result has the opposite sign. Adding two positive numbers must give a positive result Adding two negative numbers must give a negative result Overflow never occurs when adding operands with different signs. Overflow occurs if (+A) + (+B) = −C (−A) + (−B) = +C Example: Using 4-bit Two's Complement numbers (−8 ≤ x ≤ +7) (-7) + (-6) = (-13) but Overflow (largest −ve number is −8) Sem11415_hkm Overflow Rule for addition Example: Using 4-bit Two's Complement numbers (−8 ≤ x ≤ +7) (-7) + (-6) = (-13) but Overflow (largest −ve number is −8) -7 = 1001 Overflow occurs -6 = 1010 1001 + 1010 -----------1 0011 (3) The sign bit has changed to +ve Sem11415_hkm Overflow Rule for Subtraction If 2 Two's Complement numbers are subtracted, and their signs are different, then overflow occurs if and only if the result has the same sign as the subtrahend. Overflow occurs if result has the same sign as the (+A) − (−B) = −C subtrahend overflow happens (−A) − (+B) = +C Example: Using 4-bit Two's Complement numbers (−8 ≤ x ≤ +7) Subtract −6 from +7 (i.e. 7 – (-6)) subtrahend result (+A) − (−B) = −C Sem11415_hkm Overflow Rule for Subtraction Example: Using 4-bit Two's Complement numbers (−8 ≤ x ≤ +7) Subtract −6 from +7 (i.e. 7 – (-6)) 7 = 0111 Overflow occurs 6 = 0110 0111 + 0110 -----------1101 (-3) Result has same sign as subtrahend (-6) Sem11415_hkm Binary Multiplication Rules of Binary Multiplication 0x0=0 0x1=0 1x0=0 1 x 1 = 1, and no carry or borrow bits x Multiplicand Multiplier Product . Sem11415_hkm 2's Complement Multiplication Two's complement multiplication follows the same rules as binary multiplication. Example : (-4) × 4 = (-16) 4 = 00000100 -4 = 11111100 11111100 x 00000100 Ignore ----------------------11 11110000 (-16) CHECK! -16 = 11110000 Step1 : 00001111 Step2 : 00001111 + 1 ----------------------00010000 (16) Sem11415_hkm Example: Multiply the decimal numbers of 100010 by 100110 If we ignore the sign bits, the length of multiplication of an n-bit multiplicand and an mbit multiplier is a product that is (n+m) bit long. 100010 x 100110 1000 0000 0000 1000 100100010 Multiplicand Multiplier . Product Sem11415_hkm A Multiplication Algorithm and Hardware • Multiplication must cope with overflow because we frequently want a 32-bit product as the result of multiplying two 32-bit numbers. • In the next slides, assume that we are multiplying only positive number with the 1st version of highly optimized multiply hardware. Sem11415_hkm 1st Version of Multiplication Hardware 32-bit multiplicand starts at right half of multiplicand register Multiplicand Shift left 64 bits Multiplier Shift right 64-bit ALU 32 bits Product Write Control test 64 bits Product register is initialized at 0 Multiplicand register, product register, ALU are 64-bit wide; multiplier register is 32-bit wide Sem11415_hkm Flows of 1st Version Multiplication Start Algorithm Multiplier0 = 1 1. Test Multiplier0 Multiplier0 = 0 1a. Add multiplicand to product and place the result in Product register 2. Shift the Multiplicand register left 1 bit 3. Shift the Multiplier register right 1 bit 32nd repetition? No: < 32 repetitions Yes: 32 repetitions Done Sem11415_hkm Example : Using 4-bit numbers, multiply 210 x 310. Multiplicand (MC) Multiplier (MP) 2x3=? 00102 x 00112 Start Multiplier0 = 1 1. Test Multiplier0 Multiplier0 = 0 Product (P) 1a. Add multiplicand to product and place the result in Product register Steps: 1a – test multiplier (0 or 1) If 1 then P = P + MC If 0 then no operation 2 – shift MC left 3 – shift MP right All bits done? If still <max bit, repeat If = max bit, stop 2. Shift the Multiplicand register left 1 bit 3. Shift the Multiplier register right 1 bit 32nd repetition? No: < 32 repetitions Yes: 32 repetitions Done Sem11415_hkm Example : 2 x 3 Iteration 0 Step Initial value Multiplier (MP) 0011 Multiplicand (MC) 0000 0010 1a:1P = P + MC 1 0000 0100 0001 1a:1P = P + MC 2 0000 0110 2: Shift MC left 3: Shift MP right 0000 1000 0000 1a:0no operation 3 2: Shift MC left 3: Shift MP right 0001 0000 0000 1a:0no operation 4 2: Shift MC left 3: Shift MP right 0000 0000 0000 0010 2: Shift MC left 3: Shift MP right Product (P) 0010 0000 0000 41 6 Example : 5 x 4 Iteration 0 Step Initial value Multiplier (MP) 0100 Multiplicand (MC) 0000 0101 Product (P) 0000 0000 1a:0no operation 1 2: Shift MC left 3: Shift MP right 0000 1010 0010 1a:0no operation 2 2: Shift MC left 3: Shift MP right 0001 0100 0001 1a:1P = P + MC 3 0001 0100 2: Shift MC left 3: Shift MP right 0010 1000 0000 1a:0no operation 4 2: Shift MC left 3: Shift MP right 0101 000 0000 20 Example : 2 x (-3) Iteration 0 get additive inverse of both numbers (-2) x 3 Step Initial value Multiplier (MP) 0011 Multiplicand (MC) 1111 1110 1a:1P = P + MC 1 1111 1100 0001 1a:1P = P + MC 2 1111 1010 2: Shift MC left 3: Shift MP right 1111 1000 0000 1a:0no operation 3 2: Shift MC left 3: Shift MP right 1111 0000 0000 1a:0no operation 4 2: Shift MC left 3: Shift MP right 0000 0000 1111 1110 2: Shift MC left 3: Shift MP right Product (P) 1110 0000 0000 -6 Aside In the previous example only 4-bit numbers were used Larger number (with more bits) will follow the same steps Please remember to do an additive inverse for negative numbers The number of iterations are equal to the number of bits (for the numbers) 4-bit numbers = 4 iterations Try it out with these 6-bit numbers 21 x 14 21 x (-14) Sem11415_hkm Division Two operands called dividend and divisor, the result as quotient with secondary result called remainder. Divisor Quotient Dividend ... ... Remainder . . Sem11415_hkm Division • Another way to express the relationship between the components: where the remainder is smaller than the divisor. • Infrequently, programs use the divide instruction just to get the remainder, ignoring the quotient. Sem11415_hkm 1st Version of Division Hardware Divisor starts at left half of divisor register 32-bit divisor starts at left half of divisor register Divisor Shift right Quotient register is initialized to be 0 64 bits Quotient Shift left 64-bit ALU 32 bits Remainder Write Control test 64 bits Remainder register is initialized with the dividend at right Divisor register, remainder register, ALU are 64-bit wide; quotient register is 32-bit wide Flows of 1st Version Division Start 1. Subtract the Divisor register from the Remainder register and place the result in the Remainder register Remainder –> 0 Test Remainder 2a. Shift the Quotient register to the left, setting the new rightmost bit to 1 Remainder < 0 2b. Restore the original value by adding the Divisor register to the Remainder register and place the sum in the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to 0 3. Shift the Divisor register right 1 bit 33rd repetition? Algorithm No: < 33 repetitions Yes: 33 repetitions Done Example : Using 4-bit numbers, divide 710 by 210. Quotient (Q) 7/2=? 01112 x 00102 Dividend (DD) Divisor (D) Start 1. Subtract the Divisor register from the Remainder register and place the result in the Remainder register Remainder –> 0 Test Remainder Remainder < 0 Steps: 2a. Shift the Quotient register to the left, 2b. Restore the original value by adding 1 – Remainder (R) = R – D setting the new rightmost bit to 1 the Divisor register to the Remainder register and place the sum in the 2 – test new R (>=0 or <0) Remainder register. Also shift the Quotient register to the left, setting the 2a - If >=0 then new least significant bit to 0 R = no operation; Q = Shift left (add 1 at LSB) 2b - If <0 then 3. Shift the Divisor register right 1 bit R=D+R Q = Shift left (add 0 at LSB) No: < 33 repetitions 33rd repetition? 3 – shift D right All bits done? Yes: 33 repetitions If still <(max bit + 1), repeat Done If = (max bit+1), stop Divisor starts at left half of divisor register Example: 7/2 Iterat ion 0 1 Quotient (Q) Step Initial value 0000 0000 0111 1110 0111 2b. R < 0; R = D + R 0000 0111 Q = Shift left (add 0 at LSB) 0000 0001 0000 1. R = R - D 1111 0111 2b. R < 0; R = D + R 0000 0111 Q = Shift left (add 0 at LSB) 0000 3. D = Shift right 3 0010 0000 Remainder ( R) 1. R = R - D 3. D = Shift right 2 Divisor (D) 0000 1000 1. R = R - D 1111 1111 2b. R < 0; R = D + R 0000 0111 Q = Shift left (add 0 at LSB) 3. D = Shift right 0000 50 0000 0100 Iterati on 3 Step Quotient (Q) Divisor (D) 1. R = R - D 1111 1111 2b. R < 0; R = D + R 0000 0111 Q = Shift left (add 0 at LSB) 0000 3. D = Shift right 0000 0100 1. R = R - D 4 0000 0011 2a. R >=0; R = no operation Q = Shift left (add 1 at LSB) 0001 3. D = Shift right 0000 0010 1. R = R - D 5 Remainder ( R) 0000 0001 2a. R >=0; R = no operation Q = Shift left (add 1 at LSB) 3. D = Shift right 1 0011 3 Example: 7/2 = 3 remainder 1 0000 0001 Example: 6/3 Iterat ion 0 1 Quotient (Q) Step Initial value 0000 0000 0110 1101 0110 2b. R < 0; R = D + R 0000 0110 Q = Shift left (add 0 at LSB) 0000 0001 1000 1. R = R - D 1110 1110 2b. R < 0; R = D + R 0000 0110 Q = Shift left (add 0 at LSB) 0000 3. D = Shift right 3 0011 0000 Remainder ( R) 1. R = R - D 3. D = Shift right 2 Divisor (D) 0000 1100 1. R = R - D 1111 1010 2b. R < 0; R = D + R 0000 0110 Q = Shift left (add 0 at LSB) 3. D = Shift right 0000 52 0000 0110 Iterati on 3 Step Quotient (Q) Divisor (D) 1. R = R - D 1111 1010 2b. R < 0; R = D + R 0000 0110 Q = Shift left (add 0 at LSB) 0000 3. D = Shift right 0000 0110 1. R = R - D 4 0000 0000 2a. R >=0; R = no operation Q = Shift left (add 1 at LSB) 0001 3. D = Shift right 5 Remainder R) 0000 0011 1. R = R - D 1111 1101 2a. R < 0; R = D + R 0000 0000 Q = Shift left (add 0 at LSB) 3. D = Shift right Example: 6/3 = 2 0 0010 2 0000 0001 ( Signed Division Signed divide: • make both divisor and dividend positive and perform division • negate the quotient if divisor and dividend were of opposite signs • make the sign of the remainder match that of the dividend • this ensures always • dividend = (quotient × divisor) + remainder quotient (x/y) = quotient (– x/y) 7/2 Dividend = 7 Divisor = 2 Quotient = 3 Remainder = 1 -7/2 Dividend = -7 Divisor = -2 Quotient = -3 Remainder = -1 Use the value from previous calculation Sem11415_hkm