* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Unconventional signals oscillators
Yagi–Uda antenna wikipedia , lookup
Broadcast television systems wikipedia , lookup
Analog television wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Schmitt trigger wikipedia , lookup
Surge protector wikipedia , lookup
Power MOSFET wikipedia , lookup
Phase-locked loop wikipedia , lookup
Electronic engineering wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Wilson current mirror wikipedia , lookup
Oscilloscope history wikipedia , lookup
Power electronics wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
RLC circuit wikipedia , lookup
Operational amplifier wikipedia , lookup
Index of electronics articles wikipedia , lookup
Two-port network wikipedia , lookup
Radio transmitter design wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Regenerative circuit wikipedia , lookup
Rectiverter wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
BRNO
UNIVERSITY
OF TECHNOLOGY
VYSOKÉ
UČENÍ TECHNICKÉ
V BRNĚ
VYSOKÉ
UČENÍ TECHNICKÉ
V BRNĚ
BRNO UNIVERSITY
OF TECHNOLOGY
BRNO UNIVERSITY OF TECHNOLOGY
FACULTY
OF ELECTRICALA
FAKULTA
KOMUNIKAČNÍCH
FAKULTA ELEKTROTECHNIKY
ELEKTROTECHNIKY
A ENGINEERING
KOMUNIKAČNÍCH AND
TECHNOLOGIÍ
TECHNOLOGIÍ
COMMUNICATION
ÚSTAV
ÚSTAV RADIOELEKTRONIKY
RADIOELEKTRONIKY
ÚSTAV
RADIOELEKTRONIKY
FACULTY OF ELECTRICAL ENGINEERING AND COMMUNICATION
FACULTY OF
ELECTRICAL ENGINEERING
AND COMMUNICATION
FAKULTA
ELEKTROTECHNIKY
A KOMUNIKAČNÍCH
DEPARTMENT
OF
RADIO
ELECTRONICS
DEPARTMENT OF RADIO ELECTRONICS
TECHNOLOGIÍ
DEPARTMENT OF RADIO ELECTRONICS
ANALOGOVÉ OSCILÁTORY GENERUJÍCÍ
NEKONVENČNÍ SPOJITÉ SIGNÁLY
UNCONVENTIONAL
SIGNALS
OSCILLATORS
ANALOG
ANALOG OSCILLATORS
OSCILLATORS GENERATING
GENERATING UNCONVENTIONAL
UNCONVENTIONAL CONTINUOUS-TIME
CONTINUOUS-TIME SIGNALS
SIGNALS
OSCILÁTORY GENERUJÍCÍ NEKONVENČNÍ SIGNÁLY
POJEDNÁNÍ
DOCTORAL
DOCTORAL THESIS
THESIS TOPIC
TOPIC
DOCTORAL THESIS
AUTOR PRÁCE
DOKTORSKÁ
PRÁCE
Ing. ZDENĚK HRUBOŠ
AUTHOR
AUTHOR
AUTHOR
VEDOUCÍ PRÁCE
AUTOR
PRÁCE
SUPERVISOR
SUPERVISOR
SUPERVISOR
VEDOUCÍ PRÁCE
BRNO
BRNO 2016
2016
BRNO 2016
HRUBOŠ
doc.Ing.
Ing.ZDENĚK
JIŘÍ PETRŽELA,
Ph.D.
doc. Ing. JIŘÍ PETRŽELA, Ph.D.
ABSTRACT
The doctoral thesis deals with electronically adjustable oscillators suitable for signal
generation, study of the nonlinear properties associated with the active elements used
and, considering these, its capability to convert harmonic signal into chaotic waveform.
Individual platforms for evolution of the strange attractors are discussed in detail. In the
doctoral thesis, modeling of the real physical and biological systems exhibiting chaotic
behavior by using analog electronic building blocks and modern functional devices (OTA,
MO-OTA, CCII±, DVCC±, etc.) with experimental verification of proposed structures
is presented. One part of theses deals with possibilities in the area of analog–digital
synthesis of the nonlinear dynamical systems, the study of changes in the mathematical
models and corresponding solutions. At the end is presented detailed analysis of the
impact and influences of active elements parasitics in terms of qualitative changes in the
global dynamic behavior of the individual systems and possibility of chaos destruction
via parasitic properties of the used active devices.
KEYWORDS
Dynamical system, OTA, MO–OTA, CCII±, electronic adjusting, oscillator, chaos, vector
field, state attractor, eigenvalues, eigenvectors, Poincaré section, Poincaré map, Lyapunov exponents, bifurcation diagram, circuit realizations, autonomous, nonautonomous,
practical measurement, digital control, parasitic properties.
ABSTRAKT
Dizertační práce se zabývá elektronicky nastavitelnými oscilátory, studiem nelineárních
vlastností spojených s použitými aktivními prvky a posouzením možnosti vzniku chaotického signálu v harmonických oscilátorech. Jednotlivé příklady vzniku podivných atraktorů
jsou detailně diskutovány. V doktorské práci je dále prezentováno modelování reálných
fyzikálních a biologických systémů vykazujících chaotické chování pomocí analogových
elektronických obvodů a moderních aktivních prvků (OTA, MO-OTA, CCII ±, DVCC ±,
atd.), včetně experimentálního ověření navržených struktur. Další část práce se zabývá
možnostmi v oblasti analogově – digitální syntézy nelineárních dynamických systémů,
studiem změny matematických modelů a odpovídajícím řešením. Na závěr je uvedena
analýza vlivu a dopadu parazitních vlastností aktivních prvků z hlediska kvalitativních
změn v globálním dynamickém chování jednotlivých systémů s možností zániku chaosu
v důsledku parazitních vlastností použitých aktivních prvků.
KLÍČOVÁ SLOVA
Dynamické systémy, OTA, MO–OTA, CCII±, elektronické ladění, oscilátor, chaos, vektorové pole, stavový atraktor, vlastní čísla, vlastní vektory, Poincarého sekce, Poincarého
mapa, Ljapunovovy exponenty, bifurkační diagram, obvodové realizace, autonomní, neautonomní, praktické měření, digitální řízení, parazitní vlastnosti.
HRUBOŠ, Zdeněk Unconventional signals oscillators: doctoral thesis. Brno: Brno University of Technology, Faculty of Electrical Engineering and Communication, Ústav radioelektroniky, 2016. 187 p. Supervised by doc. Ing. Jiří Petržela, Ph.D.
DECLARATION
I declare that I have elaborated my doctoral thesis on the theme of “Unconventional
signals oscillators” independently, under the supervision of the doctoral thesis supervisor
and with the use of technical literature and other sources of information which are all
quoted in the thesis and detailed in the list of literature at the end of the thesis.
As the author of the doctoral thesis I furthermore declare that, concerning the creation of this doctoral thesis, I have not infringed any copyright. In particular, I have
not unlawfully encroached on anyone’s personal copyright and I am fully aware of the
consequences in the case of breaking Regulation S 11 and the following of the Copyright
Act No 121/2000 Vol., including the possible consequences of criminal law resulted from
Regulation S 152 of Criminal Act No 140/1961 Vol.
Brno
...............
..................................
(author’s signature)
This doctoral thesis is dedicated in memory of my late grandmother, Josefa Hrubošová.
ACKNOWLEDGEMENT
I would like to express my gratitude to my supervisor doc. Ing. Jiří Petržela, Ph.D. for
giving me an opportunity to work with him and for his advice and invaluable guidance
throughout my research. Gratitude is also due to my friends Ing. Roman Šotner, Ph.D.
and Ing. Tomáš Götthans, Ph.D. for their advice and invaluable guidance throughout
my research. This thesis would have been impossible without their precious ideas and
support. Last but not least, I would like to thank my parents, Jaroslava Hrubošová and
Zdeněk Hruboš, girlfriend MVDr. Alžběta Taláková and family for their patience and
giving me the motivation to finish my studies.
Brno . . . . . . . . . . . . . . .
..................................
(author’s signature)
Faculty of Electrical Engineering
and Communication
Brno University of Technology
Technicka 12, CZ-616 00 Brno
Czech Republic
http://www.six.feec.vutbr.cz
Research described in this doctoral thesis has been implemented in the laboratories
supported byt the SIX project; reg. no. CZ.1.05/2.1.00/03.0072, operational program
Research and Development for Innovation.
Brno
...............
..................................
(author’s signature)
CONTENTS
List of symbols, physical constants and abbreviations
19
Preface
23
1 State of the Art
1.1 Active Elements Suitable for Analog Signal Processing . . . . . . . .
1.1.1 Methods of Electronic Control in Applications of Modern Active
Elements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2 Comparison of Oscillator with Electronic Control . . . . . . .
1.2 Modeling of the Real Physical and Biological Systems Exhibiting Chaotic Behavior . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1 Visualization Techniques for Quantitative Analysis of Chaos .
25
25
2 Aims of the Dissertation
32
3 Electronically Adjustable Oscillators Employing Novel Active Elements
3.1 Elements with Controlled Gain . . . . . . . . . . . . . . . . . . . . .
3.2 Oscillator Based on Negative Current Conveyors . . . . . . . . . . . .
3.2.1 Proposed Oscillators . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Simulation and Measurement Results . . . . . . . . . . . . . .
3.2.3 Parasitic Influences . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Study of 3R–2C Oscillator . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1 Proposed Oscillators . . . . . . . . . . . . . . . . . . . . . . .
3.3.2 Simulation and Measurement Results . . . . . . . . . . . . . .
3.4 Multiphase Oscillator Based on CG–BCVA . . . . . . . . . . . . . . .
3.4.1 Proposed Oscillators . . . . . . . . . . . . . . . . . . . . . . .
3.4.2 Simulation and Measurement Results . . . . . . . . . . . . . .
3.4.3 Quasi–Linear Systems vs. Chaotic Systems . . . . . . . . . . .
3.5 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
33
38
38
41
44
47
47
51
58
58
61
66
67
4 Modeling of the Real Physical and the Biological Systems
4.1 Autonomous Dynamical Systems . . . . . . . . . . . . . . .
4.2 Universal Chaotic Oscillator . . . . . . . . . . . . . . . . . .
4.2.1 Mathematical Model . . . . . . . . . . . . . . . . . .
4.2.2 Mathematical Analysis . . . . . . . . . . . . . . . . .
4.2.3 Universal Chaotic Oscillator Circuit Realization . . .
4.3 Inertia Neuron Model . . . . . . . . . . . . . . . . . . . . . .
68
68
69
69
75
76
85
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
26
28
29
4.4
4.5
4.6
4.7
4.8
4.9
4.3.1 FitzHugh–Nagumo Model . . . . . . . . . . . . . . .
4.3.2 Hindmarsh–Rose Model . . . . . . . . . . . . . . . .
4.3.3 Circuitry Realization of the Inertia Neuron . . . . . .
4.3.4 Simulation and Measurement Results . . . . . . . . .
Nóse–Hoover Thermostat Dynamic System . . . . . . . . . .
4.4.1 Circuitry Implementation of the Nóse–Hoover System
4.4.2 Simulation and Measurement Results . . . . . . . . .
Algebraically Simple Three–Dimensional ODE’s . . . . . . .
4.5.1 Mathematical Analysis . . . . . . . . . . . . . . . . .
4.5.2 Circuitry Realization . . . . . . . . . . . . . . . . . .
4.5.3 Simulation and Measurement Results . . . . . . . . .
Chaotic Circuits Based on OTA Elements . . . . . . . . . .
4.6.1 Circuitry Realization . . . . . . . . . . . . . . . . . .
Chaotic Circuit Based on Memristor Properties . . . . . . .
4.7.1 Mathematical Analysis . . . . . . . . . . . . . . . . .
4.7.2 Circuitry Realization . . . . . . . . . . . . . . . . . .
4.7.3 Simulation and Measurement Results . . . . . . . . .
Nonautonomous Dynamical Systems . . . . . . . . . . . . .
4.8.1 Van der Pol Oscillator (a) . . . . . . . . . . . . . . .
4.8.2 Shaw–Van der Pol Oscillator (b) . . . . . . . . . . . .
4.8.3 Duffing–Van der Pol Oscillator (c) . . . . . . . . . . .
4.8.4 Two–well Duffing Oscillator (d) . . . . . . . . . . . .
4.8.5 Rayleygh–Duffing Oscillator (e) . . . . . . . . . . . .
4.8.6 Ueda Oscillator (f) . . . . . . . . . . . . . . . . . . .
4.8.7 Ueda Oscillator Methematical Anlysis . . . . . . . . .
4.8.8 Circuitry Realization . . . . . . . . . . . . . . . . . .
4.8.9 Simulation and Measurement Results – Voltage Mode
4.8.10 Simulation and Measurement Results – Hybrid Mode
Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5 Analog–Digital Synthesis of the
Nonlinear Dynamical Systems
5.0.1 Mathematical Analysis . . . . . . . .
5.0.2 Circuitry Realization . . . . . . . . .
5.0.3 Simulation and Measurement Results
5.0.4 3D Grid Scrolls . . . . . . . . . . . .
5.1 Summary . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
85
86
87
89
92
96
97
98
98
101
103
104
107
110
111
115
116
118
118
118
119
119
119
119
119
124
124
127
130
.
.
.
.
.
131
. 131
. 132
. 135
. 139
. 140
6 On the possibility of Chaos Destruction via Parasitic Properties of
the Used Active Devices
141
6.1 Influences of Active Elements Parasitics . . . . . . . . . . . . . . . . . 142
6.2 Influence of Parasitic Properties of Active Elements in Circuit Based
on Inertia Neuron Model . . . . . . . . . . . . . . . . . . . . . . . . . 143
6.3 Influence of Parasitic Properties of Active Elements in Circuit Based
on Memristor Properties . . . . . . . . . . . . . . . . . . . . . . . . . 146
6.3.1 Calculation of Eigenvalues . . . . . . . . . . . . . . . . . . . . 150
6.4 Influence of Parasitic Properties of Active Elements in Circuit Based
on Sprott system . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
6.4.1 Calculation of Eigenvalues . . . . . . . . . . . . . . . . . . . . 157
6.5 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
7 Conclusion
160
References
164
LIST OF FIGURES
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
3.13
3.14
3.15
3.16
3.17
3.18
3.19
3.20
3.21
3.22
3.23
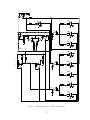
Controlled gain negative current conveyor of second generation (CCII): a) symbol, b) behavioral model. . . . . . . . . . . . . . . . . . . . . 33
Controlled gain current follower differential output buffered amplifier(CGCFDOBA): a) symbol, b) behavioral model, c) possible implementation. 34
Controlled gain current follower buffered amplifier(CG-CFBA): a)
symbol, b) behavioral model, c) possible implementation. . . . . . . . 34
Controlled gain current inverter differential output buffered amplifier
(CG-CIBA): a) symbol, b) behavioral model, c) possible implementation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
Controlled gain current amplified voltage amplifier (CG-CVA): a)
symbol, b) behavioral model, c) possible implementation. . . . . . . . 35
Controlled gain-buffered current and voltage amplifier CG-BCVA: a)
symbol, b) behavioral model, c) behavioral model with additional inverting buffer output, d) possible implementation using commercially
available ICs (version without additional inverting output). . . . . . . 36
Adjustable oscillator based on two CCII–: a) basic variant, b) resistorless variant. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
Detailed analysis of sensitivity (3.12) of oscillation frequency on product 𝐵1 𝐵2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
Time waveforms of the output signals (for 𝑉𝑆𝐸𝑇 _𝐴 = 2 𝑉 , 𝑉𝑆𝐸𝑇 _𝐵 =
0 𝑉 ), given by simulation (transient analysis in PSpice). . . . . . . . . 40
Spectrum of the output signals. . . . . . . . . . . . . . . . . . . . . . 40
Measured output signals (larger is 𝑉𝑂𝑈 𝑇 1 , smaller is 𝑉𝑂𝑈 𝑇 2 for 𝑉𝑆𝐸𝑇 _𝐴 =
2𝑉 , 𝑉𝑆𝐸𝑇 _𝐵 = 0𝑉 ).Horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣, vertical axis 500𝑚𝑉 /𝑑𝑖𝑣. 41
Measured spectrum of the output signal. . . . . . . . . . . . . . . . . 42
Oscillation frequency versus control voltage. . . . . . . . . . . . . . . 42
Output voltages vs. oscillation frequency (measured). . . . . . . . . . 43
THD versus oscillation frequency (measured). . . . . . . . . . . . . . 43
Important parasitic influences of CCII– . . . . . . . . . . . . . . . . . 44
Important parasitic influences in the proposed oscillator. . . . . . . . 44
The first proposed oscillator. . . . . . . . . . . . . . . . . . . . . . . . 48
The second version of the oscillator. . . . . . . . . . . . . . . . . . . . 49
Third version of oscillator with direct electronic adjusting. . . . . . . 50
Non-ideal models of used active elements: a) CG-CFBA, b) CG-CIBA. 51
Non-ideal models of used active elements: a) CG-CFDOBA, b) CGBCVA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Important parasitic influences in the circuit of the second oscillator. . 52
3.24 Second version of the oscillator with AGC. . . . . . . . . . . . . . . . 53
3.25 Measured results - transient responses. Horizontal axis 200𝑛𝑠/𝑑𝑖𝑣,
vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣. . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.26 Measured results - spectrum of 𝑉𝑂𝑈 𝑇 2 . . . . . . . . . . . . . . . . . . 54
3.27 Results of tuning process - dependence of THD on oscillation frequency
𝑓0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
3.28 Dependence of 𝑓0 on controlled current gain 𝐵1 . . . . . . . . . . . . . 55
3.29 Results of tuning process - dependence of output levels on oscillation
frequency 𝑓0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.30 Dependence of 𝑉𝑂𝑈 𝑇 1 on controlled current gain 𝐵1 . . . . . . . . . . . 56
3.31 Basic solution of tunable multiphase oscillator employing two active
elements based on controlled gains. . . . . . . . . . . . . . . . . . . . 58
3.32 Modification solution of tunable multiphase oscillator employing two
active elements based on controlled gains for differential quadrature
signal generation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.33 Model of proposed oscillator for non–ideal analysis. . . . . . . . . . . 60
3.34 Transient responses at all available outputs (𝑉𝑂𝑈 𝑇 1 - blue color, 𝑉𝑂𝑈 𝑇 1𝑖
- green color, 𝑉𝑂𝑈 𝑇 2 - red color, 𝑉𝑂𝑈 𝑇 3 - orange color) for 𝐵1,2 =
1.1 (𝑉𝑓0 _𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 1.15 𝑉 ). Horizontal axis 50 𝑛𝑠/𝑑𝑖𝑣, vertical axis
50 𝑚𝑉 /𝑑𝑖𝑣. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
3.35 Transient responses at 𝑉𝑂𝑈 𝑇 1 and 𝑉𝑂𝑈 𝑇 2 for 𝐵1,2 = 2.9 (𝑉𝑓0 _𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 3.17𝑉 ).
Horizontal axis 20 𝑛𝑠/𝑑𝑖𝑣, vertical axis 50 𝑚𝑉 /𝑑𝑖𝑣. . . . . . . . . . . 62
3.36 Amplitude-automatic gain control circuit for wideband amplitude stabilization. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
3.37 Measured frequency spectrum of 𝑉𝑂𝑈 𝑇 1 . . . . . . . . . . . . . . . . . . 63
3.38 Measured frequency spectrum of 𝑉𝑂𝑈 𝑇 2 . . . . . . . . . . . . . . . . . . 64
3.39 Dependence of 𝑓0 on adjustable current gains 𝐵1,2 . . . . . . . . . . . . 64
3.40 Additional characteristics - output levels (𝑉𝑂𝑈 𝑇 1 , 𝑉𝑂𝑈 𝑇 2 ) versus 𝑓0 . . . 65
3.41 Additional characteristics - THD versus 𝑓0 . . . . . . . . . . . . . . . . 65
4.1 PWL function. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
4.2 Numerical analysis of three different systems configurations from Tab.
4.1 - projection X-Y. Initial condition 𝑖𝑐 = [0.05, 0, 0]𝑇 , DS-ECEC
(top), CH2 -ECEC (center), CH3 -ECEC (bottom). . . . . . . . . . . . 73
4.3 Bifurcaion diagrams (left) and Poincaré map (right) of three selected
systems configurations from Tab. 4.1, where 𝑒32 is adopted as a bifurcation parameter. DS–ECEC (top), CH2 –ECEC (center), CH3 –ECEC
(bottom). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
4.4 Example of block for setting system parameters 𝑒𝑥 . . . . . . . . . . . 76
4.5 Universal chaotic oscillator schematic. . . . . . . . . . . . . . . . . . . 77
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20
4.21
4.22
4.23
4.24
Plane projections, the first row of the Tab. 4.1. . . . . . . . . . . . .
Plane projections, the second row of the Tab. 4.1. . . . . . . . . . .
Plane projections, the third row of the Tab. 4.1. . . . . . . . . . . .
Plane projections, the fourth row of the Tab. 4.1. . . . . . . . . . .
Plane projections, the fifth row of the Tab. 4.1. . . . . . . . . . . .
Plane projections, the eight row of the Tab. 4.1. . . . . . . . . . . .
Plane projections, the ninth row of the Tab. 4.1. . . . . . . . . . . .
Plane projections, the tenth row of the Tab. 4.1. . . . . . . . . . . .
Plane projections, the thirteen row of the Tab. 4.1. . . . . . . . . .
Plane projections, the sixteenth row of the Tab. 4.1. . . . . . . . . .
Experimental results, the first row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the second row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 2 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the third row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the fourth row of the table Tab. 4.1. Horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣,
vertical axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the fifth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the eighth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the ninth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the twelfth row of the Tab. 4.1.Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . .
Experimental results, the thirteenth row of the Tab. 4.1. Horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣,
vertical axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
78
78
78
79
79
79
80
80
80
81
. 81
. 81
. 82
. 82
. 82
. 83
. 83
. 83
. 84
4.25 Experimental results, the sixteenth row of the Tab. 4.1. Horizontal
axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . 84
4.26 Experimental results in time domain and power spectrum (Agilent
Infiniium). Horizontal axis 5 𝑚𝑠𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left),
horizontal axis 5 𝑚𝑠/𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . 84
4.27 Schematicm of the fully analog representation of single inertia neuron. 87
4.28 Simulated results of the inertia neuron obtained from PSpice - Monge
plane projection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
4.29 Simulated results of the qualitatively different behavior of the HR
model. 𝑎 = 2, 6; 𝑏 = 4; 𝑑 = 5; 𝜇 = 0, 01; 𝐼 = 2, 99; (𝑎) 𝑥0 = −0, 6;
(𝑏) 𝑥0 = −1, 6; (𝑐) 𝑥0 = −2, 0; (𝑑) 𝑥0 = −2, 4. . . . . . . . . . . . . . 89
4.30 Measured results of the inertia neuron – plane projection and frequency
spectrum (Agilent Infiniium). Horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis
2 𝑉 /𝑑𝑖𝑣. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
4.31 Measured results of the qualitatively different behavior of the HR
model(Agilent Infiniium). 𝑎 = 2, 6; 𝑏 = 4; 𝑑 = 5; 𝜇 = 0, 01; 𝐼 =
2, 99; (𝑎) 𝑥0 = −0, 6; (𝑏) 𝑥0 = −1, 6; (𝑐) 𝑥0 = −2, 0; (𝑑) 𝑥0 = −2, 4.
Horizontal axis 50 𝑚𝑠/𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣. . . . . . . . . . . . . 91
4.32 Numerical simulation of the Nóse-Hoover thermostat system – periodic (left side), chaotic (right side). . . . . . . . . . . . . . . . . . . . . 92
4.33 Map curve of the sensitivity to change of initial conditions for the
smooth Nóse-Hoover ADDS in the time domain. . . . . . . . . . . . . 93
4.34 Poincare map of sections 𝑦 vs. 𝑧 at plane 𝑥 = 0 of the Nóse-Hoover
thermostat system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
4.35 Bifurcation diagram of the Nóse-Hoover thermostat system, where
bifurcation parameter is sensitivity to change of initial conditions. . . 95
4.36 Circuit realization of the Nóse-Hoover thermostat system with AD844
as a non–inverting integrator. . . . . . . . . . . . . . . . . . . . . . . 95
4.37 Simulation results of the Nóse-Hoover oscillator – periodic (left side),chaotic
(right side). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
4.38 Measurements results of the Nóse-Hoover oscillator – periodic (left
side), chaotic (right side). Horizontal axis 500 𝑚𝑉 /𝑑𝑖𝑣, vertical axis
2 𝑉 /𝑑𝑖𝑣(top left), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 5 𝑉 /𝑑𝑖𝑣(top
right), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣(bottom left),
horizontal axis 5 𝑉 /𝑑𝑖𝑣, vertical axis 5 𝑉 /𝑑𝑖𝑣(bottom right) . . . . . . 97
4.39 Convergence plot of the largest Lyapunov exponents for 𝑎 = 0.42. . . 98
4.40 Bifurcation diagram of the Sprott system (4.29). . . . . . . . . . . . . 99
4.41 Numerical simulation of system (4.29) for 𝑎 = 0.37 – limit cycle (left
side) and for 𝑎 = 0.42 – chaos (right side). . . . . . . . . . . . . . . . 99
4.42 Sensitivity to initial conditions in the time domain. . . . . . . . . . . 100
4.43 Numerical simulation of system (4.29) for 𝑎 = 0.42. . . . . . . . . . . 100
4.44 Schematic of the Sprott system circuitry realization. . . . . . . . . . . 101
4.45 Numerical simulation of the Sprott system (4.29) for 𝑎 = 0.42 – chaos. 102
4.46 Measured data of realized circuit for 𝑅6 = 400Ω. Horizontal axis 𝑉1
500𝑚𝑉 /𝑑𝑖𝑣, vertical axis 𝑉2 1𝑉 /𝑑𝑖𝑣. . . . . . . . . . . . . . . . . . . . 102
4.47 Bifurcation diagram of system (4.37), bifurcation parameter is sensitivity to change of parameter 𝑎. . . . . . . . . . . . . . . . . . . . . . 105
4.48 Bifurcation diagram of system (4.38), bifurcation parameter is sensitivity to change of parameter 𝑏. . . . . . . . . . . . . . . . . . . . . . 105
4.49 Circuitry implementation of Eq.(4.37) using OPA860. The capacitors
are 470 𝑛𝐹 , the resistor is 1 𝑘Ω and except for the variable resistor
(adjustable from 0 to 1 𝑘Ω). . . . . . . . . . . . . . . . . . . . . . . . 106
4.50 Circuitry implementation of Eq.(4.38) using OPA860. The capacitors
are 470𝑛𝐹 , DC current source is 1 𝑚𝐴, the resistor is 1 𝑘Ω and except
for the variable resistor (adjustable from 0 to 1 𝑘Ω). . . . . . . . . . . 107
4.51 Simulation results for the circuit realized according to the Eq. 4.37 (see
Fig. 4.47) - 𝑅 = 950 Ω. Plane projection X-Z corresponds with plane
𝑎 in bifurcation diagram (see Fig. 4.47) - period 2. . . . . . . . . . . . 108
4.52 Simulation results for the circuit realized according to the Eq. 4.37 (see
Fig. 4.47) - 𝑅 = 800 Ω. Plane projection X-Z corresponds with plane
𝑏 in bifurcation diagram (see Fig. 4.47) - period 4. . . . . . . . . . . . 108
4.53 Simulation results for the circuit realized according to the Eq. 4.37 (see
Fig. 4.47) - 𝑅 = 785 Ω. Plane projection X-Z corresponds with plane
𝑐 in bifurcation diagram (see Fig. 4.47) - period 8. . . . . . . . . . . . 108
4.54 Simulation results for the circuit realized according to the Eq. 4.37 (see
Fig. 4.47) - 𝑅 = 735 Ω. Plane projection X-Z corresponds with plane
𝑑 in bifurcation diagram (see Fig. 4.47) - chaos. . . . . . . . . . . . . 108
4.55 Simulation results for the circuit realized according to the Eq. 4.38 (see
Fig. 4.48) - 𝑅 = 245 Ω. Plane projection X-Z corresponds with plane
𝑎 in bifurcation diagram (see Fig. 4.48) - period 2. . . . . . . . . . . . 109
4.56 Simulation results for the circuit realized according to the Eq. 4.38 (see
Fig. 4.48) - 𝑅 = 260 Ω. Plane projection X-Z corresponds with plane
𝑏 in bifurcation diagram (see Fig. 4.48) - period 4. . . . . . . . . . . . 109
4.57 Simulation results for the circuit realized according to the Eq. 4.38 (see
Fig. 4.48) - 𝑅 = 275 Ω. Plane projection X-Z corresponds with plane
𝑐 in bifurcation diagram (see Fig. 4.48) - period 8. . . . . . . . . . . . 109
4.58 Simulation results for the circuit realized according to the Eq. 4.38 (see
Fig. 4.48) - 𝑅 = 271 Ω. Plane projection X-Z corresponds with plane
𝑑 in bifurcation diagram (see Fig. 4.48) - chaos. . . . . . . . . . . . . 109
4.59 Numerical simulation in MathCAD and Poincare section (blue dots)
which is formed by 𝑥 − 𝑧 plane sliced at 𝑦 = 0 (green surface). . . . . 110
4.60 Plot of 𝑥(𝑡) versus 𝑦(𝑡) (left) and 𝑥(𝑡) versus 𝑧(𝑡) (right) plane projection of the chaotic attractor generated by Eq. (4.43) - numerical
solution. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
4.61 Time domain curve of the system system sensitivity to the changes
in initial conditions. Initial conditions: 𝑥0 = 0.1, 𝑦0 = 0, 𝑧0 = 0.1
and 𝛼 = 0.6 (continuous trace), 𝑥𝑛0 = 0.11, 𝑦𝑛0 = 0, 𝑧𝑛0 = 0.11
and 𝛼 = 0.6 (dashed trace). . . . . . . . . . . . . . . . . . . . . . . 112
4.62 Convergence plot of the largest Lyapunov exponents determined by
Eq. (4.43); 𝛼 = 0.6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
4.63 Bifurcation diagram generated by Eg. (4.43). The bifurcation parameter 𝛼 is shown on the horizontal axis of the plot. . . . . . . . . . . 114
4.64 Circuit realization of the chaotic system with OTA (OPA860), MOOTA (MAX435) and analog multiplier (AD633) based on Eq. (4.43).
Capacitors are 470nF and resistors are 𝑅1 = 15 Ω, 𝑅2 = 100 Ω. Resistor 𝑅3 should be adjustable from 0 to 1 𝑘Ω. . . . . . . . . . . . . . . 115
4.65 Simulation in PSpice with indication of the 𝑥−𝑧 plane sliced at 𝑦 = 0
(green surface) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
4.66 Plot of 𝑣𝑥 (𝑡) versus 𝑣𝑦 (𝑡) (left) and 𝑣𝑥 (𝑡) versus 𝑣𝑦 (𝑡) (right) plane
projection of the chaotic attractor – PSpice simulation. . . . . . . . . 117
4.67 Measured data of realized circuit (Fig. 4.64). Horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣,
vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣, vertical
axis 1 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
4.68 Numerical simulations of the nonautonomous dynamical systems with
a sinusoidally varying driving force. . . . . . . . . . . . . . . . . . . . 120
4.69 Divergence of nearby trajectories caused by small changes in initial
conditions in time domain. . . . . . . . . . . . . . . . . . . . . . . . . 121
4.70 Poincare maps of Ueda Attractor. . . . . . . . . . . . . . . . . . . . . 122
4.71 Bifurcation diagrams – dependence on the angular velocity of the
driven signal (left side) and dependence on the amplitude of the driven
signal (right side). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
4.72 The Ueda oscillator plane projection dependent on the change of the
driven frequency - numerical integration. . . . . . . . . . . . . . . . . 123
4.73 Circuitry implementation of the mathematical model in voltage mode. 124
4.74 The plane projections of the chaos oscillator obtained from PSpice
simulation – voltage mode. . . . . . . . . . . . . . . . . . . . . . . . .
4.75 Measured results of the chaos oscillator in voltage mode – plane projections and frequency spectrum (Agilent Infiniium). Horizontal axis
1 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣 . . . . . . . . . . . . . . . . . . . . . .
4.76 Circuitry implementation of the mathematical model in hybrid mode.
4.77 The plane projections of the chaos oscillator obtained from PSpice
simulation – hybrid mode. . . . . . . . . . . . . . . . . . . . . . . . .
4.78 Measured results of the chaos oscillator in hybrid mode – plane projections and frequency spectrum (Agilent Infiniium). Horizontal axis
1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 . . . . . . . . . . . . . . . . . . . . . .
5.1 The model of step function 𝑓 (𝑥) for 2𝑏 (black) and for 5𝑏 (gray). . .
5.2 Numerical simulation of system (5.1), the Monge’s projections 𝑉 (𝑥)
vs. 𝑉 (𝑦). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Numerical simulation of system (5.1), the Monge’s projections 𝑉 (𝑦)
vs. 𝑉 (𝑧). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.4 The block schematics of realization of equations (5.1). . . . . . . . .
5.5 The block schematics of realization of function 𝑓 (𝑥) using data converters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.6 The simulations from PSpice program, V(x)versus V(y) projections. .
5.7 The simulations from PSpice program, V(x)versus V(y) projections. .
5.8 The simulations from PSpice program, V(x)versus V(y) projections. .
5.9 1–D 4 scroll. Projections V(x) vs V(-y) (left), V(-y) vs V(z) (right).
Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal
axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . . . .
5.10 1–D 16 scroll. Projections V(x) vs V(-y) (left), V(-y) vs V(z) (right).
Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal
axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . . . . .
5.11 Measured system, 2x2 scroll. Projections V(x) vs V(-y) (left), V(-y)
vs V(z) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left),
horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . .
5.12 Measured system, 4x4 scroll. Projections V(x) vs V(-y) (left), V(-y)
vs V(z) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left),
horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right). . . . . . . . . . .
5.13 Measured system - perturbation of parrameters, 6x4 scroll (left) and
4x2 scroll (right). Projections 𝑉 (𝑥) vs. 𝑉 (−𝑦). Horizontal axis 1𝑉 /𝑑𝑖𝑣,
vertical axis 2𝑉 /𝑑𝑖𝑣 (left), horizontal axis 1𝑉 /𝑑𝑖𝑣, vertical axis 2𝑉 /𝑑𝑖𝑣
(right). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
125
126
127
128
129
132
133
133
134
134
135
136
136
137
137
137
138
138
5.14 Measured system, 6x6 scroll. Projections 𝑉 (𝑥) vs. 𝑉 (−𝑦) (left), 8x8
scroll, projections 𝑉 (𝑥) vs. 𝑉 (−𝑦) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣,
vertical axis 2𝑉 /𝑑𝑖𝑣 (left), horizontal axis 1𝑉 /𝑑𝑖𝑣, vertical axis 2𝑉 /𝑑𝑖𝑣
(right). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.15 Numerically simulated 3D (10,10,10) grid scolls. . . . . . . . . . . .
6.1 Non-ideal model of operational transconductance amplifier (OTA). .
6.2 Non-ideal model of multiple output operational transconductance amplifier (MO-OTA). . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝2 . . . . . . . . . . . . . . . . . . . . . . . . .
6.4 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.5 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.6 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝1 and 𝐺𝑝2 . . . . . . . . . . . . . . . . . . . . . . . . .
6.7 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝1 and 𝐺𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.8 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝2 and 𝐺𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.9 Circuit realization of the chaotic system with influence of parasitic
properties of active elements. . . . . . . . . . . . . . . . . . . . . .
6.10 Numerical analysis of system with memristor properties and influence of parasitic elements - projection X-Y (red-with parasitic, bluewithout parasitic). . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.11 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 parasitic conductance. . . . . . . . . . . . . . .
6.12 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of MAX435 parasitic conductance. . . . . . . . . . . . . . .
6.13 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 and MAX435 input parasitic conductances. . .
6.14 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 and MAX435 output parasitic conductances. .
6.15 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 parasitic capacitance. . . . . . . . . . . . . . .
6.16 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of MAX435 parasitic capacitance. . . . . . . . . . . . . . .
6.17 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 and MAX435 input parasitic capacitances. . . .
. 138
. 139
. 142
. 143
. 144
. 144
. 144
. 144
. 144
. 144
. 146
. 148
. 148
. 148
. 149
. 149
. 149
. 149
. 149
6.18 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 and MAX435 output parasitic capacitances. . .
6.19 Schematic of circuit realization with important parasitic influences.
6.20 Numerical analysis with influence of parasitic elements - projection
X-Y (red - with parasitic, blue - without parasitic). . . . . . . . . .
6.21 Circuit simulation with influence of parasitic elements (left - with
parasitic, right - with parasitic compensate ). . . . . . . . . . . . . .
6.22 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝2 . . . . . . . . . . . . . . . . . . . . . . . . .
6.23 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝𝑝3 . . . . . . . . . . . . . . . . . . . . . . . .
6.24 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝𝑝4 . . . . . . . . . . . . . . . . . . . . . . . .
6.25 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝𝑝3 . . . . . . . . . . . . . . . . . . . . . . . .
6.26 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝𝑝4 . . . . . . . . . . . . . . . . . . . . . . . .
6.27 Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝𝑝3 and 𝐶𝑝𝑝4 . . . . . . . . . . . . . . . . . . . . . . .
6.28 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝1 and 𝐺𝑝2 . . . . . . . . . . . . . . . . . . . . . . . . .
6.29 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝1 and 𝐺𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.30 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝1 and 𝐺𝑝4 . . . . . . . . . . . . . . . . . . . . . . . . .
6.31 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝2 and 𝐺𝑝3 . . . . . . . . . . . . . . . . . . . . . . . . .
6.32 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝2 and 𝐺𝑝4 . . . . . . . . . . . . . . . . . . . . . . . . .
6.33 Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐺𝑝3 and 𝐺𝑝4 . . . . . . . . . . . . . . . . . . . . . . . . .
6.34 Influence of parasitic conductance and capacitance on the size of the
𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝1 and 𝐶𝑝1 . . . . . . . . . . . . . . . . . .
6.35 Influence of parasitic conductance and capacitance on the size of the
𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝2 and 𝐶𝑝2 . . . . . . . . . . . . . . . . . .
6.36 Influence of parasitic conductance and capacitance on the size of the
𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝3 and 𝐶𝑝𝑝3 . . . . . . . . . . . . . . . . .
6.37 Influence of parasitic conductance and capacitance on the size of the
𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝4 and 𝐶𝑝𝑝4 . . . . . . . . . . . . . . . . .
. 149
. 151
. 153
. 154
. 154
. 154
. 154
. 154
. 155
. 155
. 155
. 155
. 155
. 155
. 156
. 156
. 156
. 156
. 156
. 156
LIST OF TABLES
4.1
4.2
4.3
Parameteres of different dynamical systems. . . . . . . . . . . . . . . 75
Position of critical points according to the system with PWL function.104
Numerically calculated eigenvalues of both systems. . . . . . . . . . . 106
LIST OF SYMBOLS, PHYSICAL CONSTANTS
AND ABBREVIATIONS
𝐴
adjustable voltage gain
A
square matrix, dimension is in most cases 3 × 3
A𝑇
transpose of a matrix A
𝐴𝑔
voltage gain
b,w columns vectors, dimension is in most cases 3 × 1
𝐵
current gain
𝐵𝑊 badnwidth
𝐶𝑂
condition of oscillation
𝐶𝑝
parasitic capacitance
𝐶𝑖𝑛_𝑂𝑇 𝐴 OTA input capacitance
𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 MO-OTA input capacitance
𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 OTA output capacitance
𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 MO-OTA input capacitance
𝑓0
oscillation frequency
𝑓𝑇
transient frequency
𝑔𝑚
transcoductance (controllable by bias current)
𝐺𝑝
parasitic admittance
I
unit matrix, dimension is in most cases 3 × 3
J
Jacobian matrix
𝑈𝑋 , 𝑈𝑌 , 𝑈𝑍 input voltage of CC (CCII) or analog multiplier
𝐼𝑆𝐸𝑇 bias control current
𝐼𝑋 , 𝐼𝑌 , 𝐼𝑍 input current of CC (CCII) or current multiplier
PWL piecewise-linear function
19
Q
quality factor
R𝑛
n-dimensional state space
𝑅𝑖𝑛_𝑂𝑇 𝐴 OTA input resistance
𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 MO-OTA input resistance
𝑅𝑝
parasitic resistance
𝑅𝑖𝑛_𝑂𝑇 𝐴 OTA output resistance
𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 MO-OTA output resistance
𝑅𝑥
intrinsic resistance (controllable by bias current)
𝑈𝑆𝐸𝑇 bias control voltage
𝑈𝑋 , 𝑈𝑌 , 𝑈𝑍 input voltage of CC (CCII) or analog multiplier
w𝑇
transpose of a vector w
ẋ
derivative of a function x
x0
vector of initial conditions
·
scalar product of vectors
→
right side results from left side
ADS autonomous dynamical system
NDS nonautonomous dynamical system
ADDS autonomous deterministic dynamical system
NDDS nonautonomous deterministic dynamical system
CH this chaotic attractor is typical for class C or L of dynamical systems,
corresponding with his shape attractor is socalled “single-scroll”
DS
this chaotic attractor is typical for class C of dynamical systems,
corresponding with his shape attractor is socalled “double–scroll”
CDCD this chaotic attractor is typical for class C or L of dynamical systems,
whose state matrix are in block triangular form and contain a complex
decomposed second-order submatrix
20
ECEC chaotic attractor is typical for class C or L of dynamical systems, whose
state matrix are in block triangular form and contain an elementary
canonically decomposed of second order submatrix
VB voltage buffer
VF
voltage follower
CA current amplifier
CC current conveyor
OTA operational transconductance amplifier
MO-OTA multi-output operational transconductance amplifier
DO-OTA dual output OTA
CCI first generation current conveyor
CCII second generation current conveyor
CCCII translinear current conveyor/ current controlled CCII
CCTA current conveyor transconductance amplifier
CCCTA current controlled current conveyor transconductance amplifier
CCCDTA current controlled CDTA
DCCF digitally controlled current follower
CDBA current differencing buffered amplifier
CDTA current differencing transconductance amplifier
MCDTA modified CDTA
CFA current feedback amplifier
CC-CFA current controlled current feedback amplifier
DBTA differential-input buffered and transconductance amplifier
DO-CCII/CCCII dual output CCII/ dual output CCCII
MO-CCII/CCCII multiple output CCII/ multiple output CCCII
21
ECCII/CCII electronically controllable current conveyor of second generation/
current conveyor of second generation
DVCC differential voltage current conveyor
GCFTA generalized current follower transconductance amplifie
MCDTA modified CDTA
OPAMP operational amplifier
VDIBA voltage differencing inverting buffered amplifier
CG-BCVA controlled gain buffered current and voltage amplifier
CG-CFDOBA controlled gain current follower differential output buffered
amplifier
CG-CIBA controlled gain current inverter buffered amplifier
CG-ICVA controlled gain inverted current and voltage amplifier
DCC-CFA double current controlled - current feedback amplifier
DCCF digitally controlled current follower
ZC-CG-CDBA Z-copy controlled gain current differencing buffered amplifier
PCA programmable current amplifier
22
PREFACE
„In truth at first Chaos came to be, but next wide-bosomed Earth. . . “
Hesiod’s Theogony
Chaotic motion is a very specific solution of a nonlinear dynamics systems
which commonly exists in nature. Its wide area of applications ranges from simple predator–prey models to complicated signal transduction pathways in biological
cells, from the motion of a pendulum to complex climate models in physics, and
beyond that to further fields as diverse as chemistry (reaction kinetics), economics,
engineering, sociology or demography. In particular, this broad scope of applications has provided a significant impact on the theory of dynamical systems itself, and
is one of the main reasons for its popularity over the last decades [126]. It came
as a surprise to most scientists when Lorenz in 1963 discovered chaos in a simple
system of three autonomous ordinary differential equations with a two quadratic
nonlinearities [87].
The solutions of the considered dynamical systems are a state trajectories which
are usually displayed in the state area or extended in time. Each autonomous deterministic dynamical system (ADDS) and non–autonomous deterministic dynamical
system (NDDS) are fully described by a set of differential equations and initial conditions. Behavior of the ADDS and NDDS should be completely predictable in every
time (point of view is that system should go determine by using the phase flow in
every time). Nevertheless, it is true for a linear ADDS and NDDS. In this case the
solution can be only a limit point or a limit cycle enclosed in a final volume. Suggest
that for some a special nonlinear systems, this long-term prediction of the position
can not be done. The problem is in extreme sensitivity to initial conditions in which
case is completely different pattern for the small variation in the state trajectory.
For classical autonomous dynamical systems the basic law of evolution is static
in the sense that the environment does not change with time. However, in many
applications such a static approach is too restrictive and a temporally fluctuating
environment favorable. For example, the parameters in real–world situations are
rarely constant over time. This has various reasons, like absence of lab conditions,
adaption processes, seasonal effects, changes in nutrient supply, or an intrinsic background noise. It must be noted that in practice there is always a particular degree
of imprecision in setting of the initial conditions. It all leads to study infuence of
parasitic properties.
Two basic requirements must be meet for beginning of the chaotic oscillations.
The first of them was believed to be an unstable hyperbolic fixed point which guarantee that two trajectories going in the neighbourhood are repelled from each other.
23
Divergence of two trajectories be call in this case as a "stretching". This process guarantee sensitivity to initial conditions of the system. In this way is also necessary
to eliminate expansion of the system by using curvature of the vector space by
non-linear functions. It is call as a "folding". Whereas that two distinct state space
trajectories cannot intersect, chaotic ADDS must have at least three state variables.
We can say that chaotic attractor is not periodic nor stochastic, however is bounded
and looks as a particular element of randomness. Nonlinearity can be represented as
multiply of two state variables, the power of one or as a piecewise linear function,
etc. This is important also in the case of various electronic circuits. Chaos has been
observed in the oscillators with frequency dependent feedback, oscillators with negative resistance elements, etc. The problems covered by chaos theory are universal
and can be also observed in the nonautonomous nonlinear dynamical systems with
at least two degrees of freedom. There exist many examples where chaos is unwanted phenomenon and can be observed in the networks which are basically linear, for
example in filters, oscillators, etc.
24
1
STATE OF THE ART
In this chapter we present the state of the art in the field of active elements suitable
for analog signal processing and modeling of the real physical, biological systems
exhibiting chaotic behavior by using analog electronic circuits and techniques for
visualization and quantification of chaos.
1.1
Active Elements Suitable for Analog Signal
Processing
Many active elements that are suitable for analog signal processing were introduced
in [15]. Some of them have interesting features, which allow electronic control of their
parameters. Therefore, these elements have also favorable features in applications.
There are several common ways of electronic control of parameters in particular
applications. Development in this field was started with discovery and development
of current conveyors (CC) by Smith and Sedra [144, 145], Fabre [30] and Svoboda
et al. [167]. Many other active elements with possibilities of electronic adjustability
were introduced, innovated and frequently utilized for circuit synthesis and design
in the past, for example operational transconductance amplifier (OTA) [38], current
feedback amplifiers (CFA) [15, 107, 136], etc. Great review of old and also recent
discoveries in the field of active elements was summarized by Biolek et al. [15].
Extensive description of many modifications and novel approaches is given in [15]
and in references cited therein.
1.1.1
Methods of Electronic Control in Applications of Modern Active Elements
Basic way how to control parameters in applications is by manual change of values
of passive elements - floating or grounded resistors in most cases (see [39, 44, 47,
91, 95, 149], for example). Electronic control requires additional element (e.g. FET
transistor [39]) and the final solution is more complicated generally. Better way is to
use so-called bias currents for direct electronic control of parameters of active elements (OTA-s, CC-s, ...). Adjusting of the intrinsic resistance (RX) by bias current
(Ibias) is very common solution of control of parameters of many application employing current conveyors [11, 27, 32, 53, 131] or adjustable current feedback amplifiers
[142, 152, 150]. Similarly, adjusting of the transconductance value of the OTA [38]
also requires bias current control [12, 20, 36, 77, 79, 84, 130, 141, 147, 153, 170].
25
The next method which is used is the current gain adjusting. Development of this
method has been started together with development of so-called current followers
(CF) [15] and its derivatives [1, 16, 40, 41, 53, 94, 148]. Applications of adjustable
current followers and amplifiers (in order to control current gain) were reported in
[127, 135, 169], for example. Many authors implemented current gain controlling
mechanism also to current conveyors and amplifiers [31, 46, 75, 76, 93, 99, 139, 156,
166, 168]. Several conceptions also utilize combination of two methods of adjusting
(two parameters) [76, 93, 99]. Minaei et al. [99], Kumngern et al. [76] and Sotner et
al. [152, 150] presented several different design methods of current conveyors with
possibility of intrinsic resistance and current gain control, Marcellis et al. [93] has
designed conveyor with simultaneous adjusting of current and voltage gain. Digital
control of current gain achieved increasing attention in recent years. El-Adawy et al.
[26] and Alzaher et al. [5, 6, 7] introduced digitally programmable current followers,
amplifiers and current conveyors, respectively.
1.1.2
Comparison of Oscillator with Electronic Control
A short comparison of several oscillator realizations with electronic control is given
at this place.
Sotner et al. [150] engaged three so-called double current-controlled current feedback amplifiers (DCC-CFA) in quadrature oscillator solution. Circuit has advantages of non-interactive electronic controllability of condition of oscillation (CO) and
oscillation frequency (𝑓0 ) without impact on changes of output amplitudes during
the tuning process. All parameters of the oscillator are controllable electronically by
bias currents (current-gains) and additional extension of tunability range is possible
via adjustable intrinsic resistances (𝑅𝑋 ).
Three electronically controllable dual output current amplifier-based integrators
were utilized by Souliotis et al. [156] in arbitrary-multiphase (in this particular case three-phase) current-mode oscillator as an example of directly electronically tunable
oscillator. The CO and 𝑓0 are tunable by control current Ibias. A current conveyor
based integrators for generalized multiphase oscillator design were used by Kumngern et al. [75]. They also designed an internal structure of current conveyor with
adjustable current gain between X and Z terminals. Matching of time constant of
each integrator section is ensured by bias control of the current gains. Unfortunately,
results are not focused on electronic adjusting of oscillation frequency.
Kumngern et al. [76] also proposed simple oscillator where intrinsic input resistance was used for 𝑓0 and current gain for CO control (non-interactive). Only
two active elements and two grounded capacitors are necessary in their solution.
However, amplitude dependence and nonlinear control of 𝑓0 occurs. An interesting
26
solution where three programmable current amplifiers (PCAs), two resistors and two
capacitors were implemented was proposed by Herencsar et al. [46]. Dependence of
𝑓0 on current gain is not linear but 𝑓0 and CO are controllable by current gains.
Alzaher proposed very useful oscillator employing digitally adjustable active elements [5]. His oscillator allows operation in both voltage and current mode. Control
of 𝑓0 is linear and oscillation condition is also adjustable by current gain. His solution requires three adjustable elements and six passive elements. Souliotis et al.
[157] also presented two simple solutions of quadrature oscillator, where two active
elements employing current gain adjusting and two grounded capacitors were used.
The current gain type of 𝑓0 control was also used in oscillators employing so-called
Z-Copy Controlled-Gain Current Differencing Buffered Amplifier (ZC-CG-CDBA)
introduced by Biolek et al. in [9] and [14]. The solution in [9] requires two ZC-CGCDBAs and 6 passive elements. CO is controllable by floating resistor, but 𝑓0 is
adjustable digitally (dependence of 𝑓0 on current gain is linear). Solutions discussed
in [14] engage two ZC-CG-CDBAs and five passive elements and 𝑓0 is controllable
linearly. Output amplitudes are not dependent on tuning process however, CO is
controllable using floating resistors only.
Electronic control of 𝑓0 in [154] is possible by adjustable current gain, but oscillation condition is only available by controllable replacement of grounded resistor.
Oscillator in [154] employs only one active element, but its disadvantage is in the
dependence of one of produced amplitude on tuning process and nonlinear control
of 𝑓0 . Lack of electronic controllability of oscillation condition [154] was improved in
[223], where additional active element with controllable gain was used. Two similar
solutions, where active elements with low–impedance voltage outputs were utilized
in oscillator design are discussed in [222].
The digital adjusting of current and voltage gains are very useful for 𝑓0 control
([5, 9, 14], for example). However, discontinuous adjusting of CO can be insufficient
for satisfactory stability of output amplitudes and low total harmonic distortion
(THD) in some cases. Sufficient bit resolution of digital control is critical. Analog to
digital converter is essential part if digital control (derived from output amplitude)
of CO is intended for automatic amplitude gain control (AGC circuit). It causes
additional complication and increasing of power consumption. Therefore continuous
control seems to be better for adjusting of oscillation condition in order to ensure
stable output amplitudes and low THD.
27
1.2
Modeling of the Real Physical and Biological
Systems Exhibiting Chaotic Behavior
The research of many scientists and engineers is focused onto relations between the
real physical systems and its mathematical models from the viewpoint of study of
the associated nonlinear dynamical behavior. In 1963, Lorenz published a seminal
paper [87] in which he showed that chaos can occur in systems of autonomous (no
explicit time dependence) ordinary differential equations (ODEs) with as few as
three variables and two quadratic nonlinearities.
Circiut synthesis of the mathematical model is the easiest way how to accurately simulate the autonomous and the non–autonomous dynamical systems [33].
There exist several ways how to practically realize chaotic oscillators. Most of these
techniques are straightforward and have been already published [60]. The design
procedure can be based on the integrator block schematics or classical circuit synthesis [112]. Alexandre Wagemakers discuss about analog simulations and about the
possible advantages and drawbacks of using electronic circuits in his thesis [174].
Advanteges of analog simulation are evident and are many reasons why proceed to
system simulation with analog circuit. The components are not perfect and their
parameters are changed from component to component. That fact implement in a
electronic circuit means that circuit is robust to small parameter changes and is
not sensitive to these small differences. The resistance to noise is another benefits,
because the influenced of external factors, such as the temperature, are part of real
component. Advantages compared with the numerical integration are also in the
duration of the simulation and possibilities to change the parameter directly in real
time (the time constant controlled by variable resistor).
Chaos, or deterministic chaos, is ubiquitous in nonlinear dynamical systems of
the real world, including biological systems. Nerve membranes have their own nonlinear dynamics which generate and propagate action potentials, and such nonlinear
dynamics can produce chaos in neurons and related bifurcations. Neural models are
used in computational neuroscience and in pattern recognition. The aim is understanding of real neural systems. In this case, the highly parallel nature of the neural
system contrasts with the sequential nature of computer systems. It leads to slow
and complex simulation software. The circuit synthesis of a single neuron can be the
prelude to the implementation of neuromorphic hardware or neural networks and
promise of faster emulation [56, 138, 146, 163, 187, 234].
Other example from real world is Nóse–Hoover thermostat. Equations of motion have been applied to the study of fluid and solid diffusion, viscosity, and heat
conduction with computer simulation and to the nonlinear generalization of linear
28
response theory required to describe systems far from equilibrium. For continuous
flows, the Poincare-Bendixson theorem [51] implies the necessity of three variables,
and chaos requires at least one non-linearity. More explicitly, the theorem states that
the long-time limit of any “smooth” two-dimensional flow is either a fixed point or
a periodic solution [52, 121].
Chaos control and generation has a dramatic increase of interest since many
real world applications and observations in engineering or other fields have been
presented. For example in fields such as biomedical engineering, digital data encryption, power systems protection, reconfigurable hardware, and so on. But yet
there is no simple rule for quantifying chaos origin. Generating chaotic attractors
may help to understand better dynamics of real world systems. Nowadays, there
exists a lot of practical applications which are based on the chaotic oscillators. For
example in telecomunications (different coding methods such as chaotic modulation,
chaotic masking, chaotic shift keying , chaotic switching or random bit generators
[29, 37, 54, 129, 184]. From this point of view, the different ways leading to the
practical implementation of such an electronics circuits seems to be useful.
With the growing availability of powerful computers, many other examples of
chaos were subsequently discovered in algebraically simple ODEs. Example of such
system is memristor–based chaotic circuit derived by simply replacing the nonlinear
resistor in Chua’s circuit with a flux–controlled memristor [100, 101, 102] and other
circuits based on memristor properties [24, 61, 62, 111, 128, 175, 178]. There are
reasons that other simple examples with quadratic and piecewise linear nonlinearities
have been identified and mathematical models of unconventional signals oscillators
have been published in literature up to this day [59, 68, 72, 101, 159, 160, 161, 162,
171, 115]. Novel circuit realizations of chaotic systems are described in this work.
A short chapter is devoted to a new possibilities in the area of analog-digital
synthesis of the nonlinear dynamical systems. Over past three decades, generating
multi-scroll chaotic attractors became an aim of many researchers [3, 115, 118, 161,
229]. Many techniques involving different approaches (usually using comparators
or hysteresis) have been published [25, 88, 106]. In the chapter 5 the discrete step
functions are used in order to generate 𝑚𝑥𝑛 scroll chaotic hypercube attractors.
1.2.1
Visualization Techniques for Quantitative Analysis of
Chaos
In the world of chaos exist techniques used to visualization and quantification of
chaos. First of them is a bifurcation diagram. The bifurcation is defined as a qualitative change in the dynamical behavior of the system of its phase portrait as one or
more parameters are changed. Any point in the parameter set, where the behavior
29
of dynamical system is unstable is called a bifurcation point, and the set of these
points is called a bifurcation set [109]. This set can contain infinite number of the
points but usually has zero measure [159].
Other technique is a Poincaré section (map). It is very useful visualisation method to the qualitative analysis of nonlinear dynamical systems, since they provide
a lower dimensional system that still captures the essential features of the original
dynamics [35]. In the case of nonautonomous systems, the Poincaré section of a periodic solution is calculated easily because the Poincaré mapping can be defined as
mapping whose period is identical to the period of forced signal 1.1.
𝑦𝜔 =
𝑡
∑︁
𝑥𝑘 (Θ) ,
(1.1)
𝑘=1
where 𝑘 ∈ 𝑁 and Θ = 2𝑘𝜋 is forced signal period. While for autonomous systems, the
period of the limit cycle is changed as the parameters changes, so it is not suitable to
analyze the limit cycle just as nonautonomous system. Therefore we should provide
a cross–section called the Poincaré section and define the corresponding Poincaré
mapping. This method implicitly requires the accurate location of the point at which
the periodic orbit started from the cross–section returns (1.2).
𝑦𝑛 =
𝑡
∑︁
𝑥𝑘 (Θ)
(1.2)
𝑘=1
The transition surface must be perpendicular to the flow [66]. The Poincaré section
can be chosen by fixing one system state (for example 𝑧) to be constant, and the
projection of the attractor is obtained on the 𝑥−𝑦 plane [54]. The resulting map is for
limit cycles very simple – it consists of one or more isolated points, for quasi–periodic
movement it consists of a set of points on a curve bounded interval. However, for
chaotic motion we get a very complex projection which is represented a stroboscopic
cross–section of the attractor. The previous two techniques are used usually for chaos
vizuoalization.
Another technique, Lyapunov exponents, provide a quantitative measurements of
the divergence or convergence of nearby trajectories for the dynamical system. If we
consider a small space of initial conditions in the phase space, for sufficiently short
time scales, the effect of the dynamics will be to distort this set into a hyperellipsoid,
stretched along some directions and contracted along others [132]. The spectrum of
the Lyapunov exponents is defined in the form
(︁
)︁
1
ln‖𝐷𝑥 Φ (𝑡, x0 ) y0 ‖,
𝑡→∞ 𝑡
𝐿𝑒𝑥 x0 , y0 ∈ 𝑇 x(𝑡)𝑅3 = lim
(1.3)
where 𝑇 x(𝑡) is a tangent space in the point on the fiducial trajectory and y(𝑡) =
𝐷𝑥 Φ (𝑡, x0 ) y0 is solution of the linearized system [132]. The usual test for chaos is
30
calculation of the largest Lyapunov exponent (𝐿𝐸𝑚𝑎𝑥 ) and a positive value indicates chaos [159]. There are just three 𝐿𝐸𝑚𝑎𝑥 and each is a real number giving the
average ratio of exponential divergency of the two neighborhood trajectories. Since
one 𝐿𝐸𝑚𝑎𝑥 must be close to zero (direction of the flow) to obtain sensitivity to the
initial conditions (chaos) it is necessary to have one LE positive. The last LE must
be negative with the largest absolute value to preserve dissipation. These techniques
are used in this work and presented with numerical analysis of some systems in
chapter 4.
31
2
AIMS OF THE DISSERTATION
We can still find areas where can be our focus concentrated in view of the fact that
the possibility of the implementation and application of chaotic oscillators are not
fully explored and exhausted yet. Structure of the dissertation thesis is divided into
four areas and the main aims can be summarized into these categories:
∙ Electronically adjustable oscillators suitable for signal generation employing
active elements, study of the nonlinear properties of the active elements used,
platform for evolution of the strange attractors.
∙ Modeling of the real physical and biological systems exhibiting chaotic behavior by using analog electronic circuits and modern functional blocks (OTA,
MO-OTA, CCII±, DVCC±, etc.) with experimental verification of proposed
structures.
∙ Research a new possibilities in the area of analog-digital synthesis of the nonlinear dynamical systems, the study of changes in the mathematical models and
corresponding solutions.
∙ Detailed analysis of the impact and influences of active elements parasitics in
terms of qualitative changes in the global dynamic behavior of the individual
systems and possibility of chaos destruction via parasitic properties of the used
active devices.
32
3
ELECTRONICALLY ADJUSTABLE OSCILLATORS EMPLOYING NOVEL ACTIVE ELEMENTS
3.1
Elements with Controlled Gain
Many modern active functional blocks are available for application in analog technology and signal processing in the present time. This fact is discussed in paper [15]
where the review and basic theory of the novel blocks are given. One of them is negative current conveyor of second generation CCII- (Fig. 3.1) which we used in very
simple oscillator circuitry. The principle of this block is clear from Fig. 3.1. The
VSET
Y
VSET
IY = 0
VY
VX
(0 – 2 V)
1
B = f(VSET)
Y
CCII-
IX
IZ
Z
VZ
Z
Ix
X
Iz = -B.Ix
Rx
B = f(VSET) IZ = -B.IX
X
(a)
95 Ω
(b)
Fig. 3.1: Controlled gain negative current conveyor of second generation (CCII-): a)
symbol, b) behavioral model.
negative three–port current conveyor CCII– with adjustable current gain has the
symbol shown in Fig. 3.1a, where the port variables are denoted. This block can be
described in a classical way [15]. The important relations are written in this figure,
too. There is current input 𝑋, voltage input 𝑌 and current output 𝑍. Compared to
common types of the CCII (e.g. AD844 [191]) this conveyor has the possibility of
electronic controlling of the current gain 𝐵. For design and verification, commercially available CCII– (obsolete but sufficient for experiments) was used. This device
is commercially available as EL2082 as two–quadrant current–mode multiplier [193].
The gain control input is calibrated to 1 𝑚𝐴/𝑚𝐴 signal gain (𝐵) for 1 𝑉 of control
voltage 𝑉𝑆𝐸𝑇 (see [193]), else 𝐵 = 𝑓 (𝑉𝑆𝐸𝑇 ) and simplification is valid approximately
(example: 𝑉𝑆𝐸𝑇 = 2 𝑉 means that exactly 𝐵 = 1.9).
Biolkova et al. [16] introduced other novel active element, so–called dual output current inverter buffered amplifier (DO-CIBA). Application field of such active
element is very spread, but possibility of direct electronic control was not discussed (direct electronic control in the frame of the active element). We used several
33
Iz
Vz
CG-CFDOBA
VSET
VSET
VSET
VSET
z
VSET
CG-CFDOBA
VSET
Vp
Vw+
w+
Ip
p
B.Ip
CG-CFDOBA
p
Iz
p
VwCG-CFDOBA
w-
Vpz
Vw+
w+
Ip
B
B.Ip
w- p
p
Vw-
w-
z
Vz
Ip
EL2082
w+
1
w+
1
w-
Ip
Iz
CG-CFDOBA
Vz
B.Ip
z
w-
CG-CFDOBA
EL2082
modified versions of DO-CIBA.
of so–called controlled gain current follower
w+
VSETSymbol
CG-CFDOBA
B
p
differential-output buffered amplifier (CG-CFDOBA)
[15] is depicted in Fig. 3.2 (a).
wEL2082
AD8138
Element contains four ports.
Basic principle is explained in Fig. 3.2 (b). Loww+
B
impedance current pinput zis labeled p, auxiliary high-impedance port as z, and buffered outputs (after voltage buffer/inverter) as w+ wand w-, respectively. The output
AD8138
current at auxiliary port (z) is positive, which means that it flows out of the terminal. The current gain (B) between
current input port (p) and auxiliary port (z)
z
can be adjusted electronically via external voltage. Possible implementation of CGCFDOBA with commercially available devices [190, 193, 194, 199, 195] is shown in
Fig. 3.2 (c).
V
Simplified version (Fig. 3.3), where only one output w is necessary, should be
w
also noted. This modification is usually called as controlled pgain current 1follower
I
B.I termibuffered amplifier (CG-CFBA) [15]. Modification, where current at auxiliary
CG-CFBA
nal (Fig. 3.4) z is inverted, is marked as controlled gain current
inverter
buffered
z
amplifier (CG-CIBA) [15, 16].
Following hybrid matrices describe generally our intention in order to obtain
SET
VSET
Ip
Vp
p
Vw
CG-CFBA w
z
p
Iz
p
Vz
VSET
VSET
VSET
VSET
CG-CFBA
VSET
Ip
Vp
p
CG-CFBA w
z
EL2082
Vw
p
Ip
Vp
p
Iz
Vw
CG-CFBA w
1
Ip
p
B
p
1
B.I
Ip
z
Vz
w
CG-CFBA
Vz
(a)
LT1364
B.Ip
z
(b)
CG-CFBA
w
w
p
Iz
z
(c)
z
Fig. 3.3: Controlled gain current follower buffered amplifier(CG-CFBA): a) symbol,
b) behavioral model, c) possible implementation.
VSET
EL2082
p
B
CG-CFBA
VSET
CG-CFBA
34
w
EL2082
p
B
LT1364
w
Rp
Ip
z
CG-CF
Fig. 3.2: Controlled gain current follower differential output buffered amplifier(CGCFDOBA): a) symbol, b) behavioral model, c) possible implementation.
VSET
p
z
Cz
(c)
z
R
AD8138
z
(b)
1
Ip
CG-CFDOBA
CG-CFDOBA
(a)
Rp
pw+
B.In
Iz
Vz
CG-CIBA
z
VSET
VSET
In
Vn
VSET
VSET
CG-CIBA
VSET
n
Vw
CG-CIBA w
EL2082
n
1
In
z
Vn
n
Iz
Vz
B
n
In
Vw
CG-CIBA w
w
n
w
1
B.In
w
LT1364
In
z
CG-CIBA
Iz
B.In
z
Vz
(b) CG-CIBA
(a)
z
(c)
z
Fig. 3.4: Controlled gain current inverter differential output buffered amplifier (CGCIBA): a) symbol, b) behavioral model, c) possible implementation.
VSET
CG-CIBA
adjustability very well.
EL2082Equation (3.1) describes the modified DO-CIBA with adVSET
CG-CIBA
B (B), equation
justable current
gain
(3.2)
n
w explains extension providing adjustable
current (B) and voltage gain (A) simultaneously
EL2082
LT1364
n
⎡
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎣
𝐼z𝑧
𝑉𝑤+
𝑉𝑤−
𝑉𝑝
𝐼𝑧
𝑉𝑤+
𝑉𝑤−
𝑉𝑝
B⎤
⎡
⎥
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎢
⎣
=
⎤
⎡
⎥
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎢
⎣
=
0
1
−1
z0
0
0
0
0
0 ±𝐵
0 0
LT1364
0 0
0 0
𝑉𝑧
𝐼𝑤+
𝐼𝑤−
𝐼𝑝
⎤
0
𝐴
−𝐴
0
0
0
0
0
𝑉𝑧
0 ±𝐵
⎥ ⎢
⎢
⎥
0 0 ⎥ ⎢ 𝐼𝑤+
⎥·⎢
⎢
0 0 ⎥
⎦ ⎣ 𝐼𝑤−
𝐼𝑝
0 0
⎤
⎤ ⎡
w
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥·⎢
⎥ ⎢
⎦ ⎣
⎤ ⎡
⎥
⎥
⎥
⎥,
⎥
⎦
(3.1)
⎥
⎥
⎥
⎥.
⎥
⎦
(3.2)
General adjustable element can be created if adjustable voltage amplifier is used
instead of voltage buffer (Fig. 3.5). It provides full control, i.e. current gain (B)
and voltage gain (A). We called this element as controlled gain current and voltage
amplifier (CG-CVA). Version with inverting current amplifier is called controlled
VSET_B
VSET_B
VSET_A
VSET_B VSET_A
EL2082
B.Ip
Ip
Vp
p CG-CVA w
VSET_A
Vw
pA
p
Ip
w
Vw = Vz.A
p
B
A
w
VCA810
z
Iz
Vz
(a)
CG-CVA
CG-CVA
z
z
(b)
(c)
Fig. 3.5: Controlled gain current amplified voltage amplifier (CG-CVA): a) symbol,
b) behavioral model, c) possible implementation.
35
Vw = Vz.A
w
Vb = Vz
b
gain inverted current and voltage amplifier (CG-ICVA). Possible modification with
dual voltage output (w+, w-) could be called dual output controlled gain current
and voltage amplifier (DO-CG-CVA). Ideal behavior is clear from equation (3.2).
Improved conception of CFDOBA allows controllability of both current and voltage gains simultaneously in frame of one active element and it is useful approach
for design of controllable applications. We called this modification as controlled
gain-buffered current and voltage amplifier (CG-BCVA). A detailed explanation
is provided in Fig. 3.6, where symbol, behavioral models, and possible practical
implementation employing readily available ICs is shown. Terminals of presented
active element provide more possibilities than CG-CFDOBA. However, many of
them have the same purpose. Low-impedance current input terminal p, auxiliary
high-impedance terminal z, and low-impedance voltage output terminals w± have
the same meaning like in CG-CFDOBA (see Fig. 3.2). CG-BCVA has additional dispositions. As mentioned above, this active element was firstly used in [222] only theoretically in so-called controlled gain-current and voltage amplifier (CG-CVA) and
controlled gain-inverted current and voltage amplifier (CG-ICVA). The CG-CVA
and CG-ICVA use voltage amplifier with adjustable voltage gain (A) in comparison
VSET_A
VSET_B
VSET_B VSET_A
R
z
VSET_B VSET_A
Rp
p
Ip
Ip
Vp
Vp
p
Ip
Cz
B.Ip
w
Vw
w
p CG-BCVA
CG-BCVA
V
b
b
z
VSET_B VSET_A
Vw = Vz.A
A
w
Ip
Vw Vp
b
b
Vbz = V
pz
b
B.I
B.Ip p
Vw
B.Ip
Vb
p
A
Ip
Iz
z
1
Vz
I
CG-BCVA
z
Vz
w
p CG-BCVA
Vb1
z
Iz
CG-BCVA
Vz
z
(a)
Ip
CG-BCVA
p
p
Ip
CG-BCVA
A B
VSET_B
w
A
(c)CG-BCVA
B
1
w
b
CG-BCVA
BUF634
Vz
b
z
w
A
b
1
EL2082
Vb+ = Vz
Vb- = -Vz
Vb = Vz
b
Vb =
VSET_AVCA810
VCA810
p
z
1
Vz.A
w
EL2082
b+
b-
A
Vw = Vz.A
V =
w w
VSET_A
B
p
EL2082
Vw = Vz.A
1
z
VSET_A
A
1
Vb = Vz
b
CG-BCVA
(b)
VSET_B
VSET_A
B.Ip
Vw = Vz.A
wIp
p
VSET_B
VSET_B
VSET_A
VSET_A
VSET_B
VSET_B
VSET_A
VSET_B
BUF634
Az
w
(d)
z
VCA810
p
b
Fig. 3.6: Controlled gain-buffered current and voltage 1amplifier CG-BCVA: a) symBUF634
bol, b) behavioral model, c) behavioral model with additional inverting buffer outCG-BCVA
put, d) possible implementation using commercially
available ICs (version without
z
additional inverting output).
36
to CG-CFDOBA, where only voltage buffer/inverter is used. Control of current and
voltage gains is separated into two auxiliary terminals (two controlling DC voltages
- 𝑉𝑆𝐸𝑇 _𝐵 and 𝑉𝑆𝐸𝑇 _𝐴 respectively). Terminal w is low-impedance voltage output of
voltage amplifier in case of CG-CVA or CG-BCVA. The additional voltage buffer,
which can be also used as inverter, see Fig. 3.6 (c), gives interesting advantage in
multi-loop circuit synthesis. The output(s) of voltage buffer is(are) marked by b.
Ideal behavior of CG-BCVA is defined by following matrix equations:
⎡
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
𝐼𝑧
𝑉𝑤
𝑉𝑏
𝑉𝑝
𝐼𝑧
𝑉𝑤
𝑉𝑏+
𝑉𝑏−
𝑉𝑝
⎤
⎡
⎥
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎢
⎣
=
⎤
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
=
0
𝐴
1
0
0
𝐴
1
−1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
𝐵
0
0
0
0
0
0
0
0
⎤ ⎡
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥·⎢
⎥ ⎢
⎦ ⎣
𝐵
0
0
0
0
𝑉𝑧
𝐼𝑤
𝐼𝑤
𝐼𝑝
⎤ ⎡
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎥·⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢
⎦ ⎣
⎤
⎥
⎥
⎥
⎥,
⎥
⎦
𝑉𝑧
𝐼𝑤
𝐼𝑏+
𝐼𝑏−
𝐼𝑝
(3.3)
⎤
⎥
⎥
⎥
⎥
⎥,
⎥
⎥
⎥
⎦
(3.4)
where equation (3.3) represents model of CG-BCVA in Fig. 3.6 (b) and eq. (3.4)
model in Fig. 3.6 (c) respectively. Adjustable gains are very useful for oscillator
design as is obvious from designed solution presented in further text.
37
3.2
Oscillator Based on Negative Current Conveyors
In this part very simple oscillator employing two negative conveyors CCII– is presented. Oscillation frequency and condition of oscillation may be driven by varying
electronically controlled current gains 𝐵. A basic variant includes four passive components (two R and two C). Also resistor–less variant with two capacitors only is
given. Here, instead of the real resistor, the input resistance 𝑅𝑥 of the conveyor terminal 𝑋 (Fig. 3.1) is used. Note that the manufacturer guarantees the value of 𝑅𝑥
in tolerance of ±20% so this must be taken into account during the design of this
simpler variant. The output signal can be taken from two internal nodes. However,
to separate the load impedance a voltage follower can be appropriately used. On the
other hand, the disadvantage of this circuit is that one working capacitor is floating
and the oscillation frequency may be driven only in a limited range. Despite this,
implementation of the proposed circuit is simpler comparing to previous oscillators
discussed above. More current outputs are not required and a classical three–port
CC is sufficient.
3.2.1
Proposed Oscillators
The proposed tunable oscillator employing two negative conveyors CCII– is shown
in Fig. 3.7. The basic variant (Fig. 3.7a) has four passive elements, two R and two
C. In Fig. 3.7b, the resistor–less version is shown, using the input 𝑋 resistance (𝑅𝑥
in Fig. 3.1) of the real conveyor. The circuit from Fig. 3.7 has the characteristic
equation of the second-order general form
𝑎2 𝑠2 + 𝑎1 𝑠 + 𝑎0 = 0.
(3.5)
OUT2
OUT2
VSET_A
R1
VSET_A
CC1
C2
R2
CCII- Z
Y
VSET_B
CC1
VSET_B
CC2
Y
CCII- Z
X
Y
X
C1
CC2
C2
C1
CCII- Z
X
CCII- Z
Y
OUT1
(a)
X
OUT1
(b)
Fig. 3.7: Adjustable oscillator based on two CCII–: a) basic variant, b) resistor-less
variant.
38
By symbolic nodal analysis and setting of det Y = 0, the following characteristic
equation is obtained
𝑠2 +
1 − 𝐵1 𝐵2
𝐶1 𝑅1 + 𝐶2 𝑅2 (1 − 𝐵1 )
𝑠+
= 0.
𝑅1 𝑅2 𝐶1 𝐶2
𝑅1 𝑅2 𝐶1 𝐶2
(3.6)
From the characteristic equation (3.6), we can determine the oscillation condition
in the following form
𝐶1 𝑅1 + 𝐶2 𝑅2 = 𝐶2 𝑅2 𝐵1 ,
(3.7)
𝐵1 ≈ 𝑉𝑆𝐸𝑇 _𝐴 ,
(3.8)
and also the formula for the frequency of oscillations
√︃
𝜔0 =
1 − 𝐵1 𝐵2
≈
𝑅1 𝑅2 𝐶1 𝐶2
√︃
1 − 𝑉𝑆𝐸𝑇 _𝐴 𝑉𝑆𝐸𝑇 _𝐵
.
𝑅1 𝑅2 𝐶1 𝐶2
(3.9)
The sensitivities of the oscillation frequency (3.9) to the passive components and
parameters of the CC’s were found, namely
1
𝑆𝐶𝜔01 = 𝑆𝐶𝜔02 = 𝑆𝑅𝜔01 = 𝑆𝑅𝜔02 = − ,
2
𝑆𝐵𝜔01 = 𝑆𝐵𝜔02
(3.10)
1
𝑆𝑅𝜔0𝑥1 = 𝑆𝑅𝜔0𝑥2 = − ,
2
1 𝑉𝑆𝐸𝑇 _𝐴 𝑉𝑆𝐸𝑇 _𝐵
1 𝐵1 𝐵2
≈−
.
=−
2 (1 − 𝐵1 𝐵2 )
2 (1 − 𝑉𝑆𝐸𝑇 _𝐴 𝑉𝑆𝐸𝑇 _𝐵 )
(3.11)
(3.12)
From (3.7) and (3.9) it is clear that 𝐵1 is not suitable for 𝜔0 control because it is
0
-5
-10
Sensitivity
-15
-20
-25
-30
-35
-40
-45
-50
0
0.1
0.2
0.3
0.4
0.5
B1*B2
0.6
0.7
0.8
0.9
1
Fig. 3.8: Detailed analysis of sensitivity (3.12) of oscillation frequency on product
𝐵1 𝐵2 .
39
also in the condition of oscillation (3.7). However, 𝐵2 is only in (3.9) therefore it can
be theoretically suitable for 𝜔0 control. The resistance 𝑅1 in formulas above (also
𝑅2 by analogy) is given by the sum 𝑅1 = 𝑅1𝑒𝑥𝑡 + 𝑅𝑥1 . External working resistor
𝑅1𝑒𝑥𝑡 must be added to 𝑅𝑥1 , which is the input of the current port 𝑋. Note that
these virtual resistances (𝑅𝑥1 , 𝑅𝑥2 ) (without 𝑅1𝑒𝑥𝑡 , 𝑅2𝑒𝑥𝑡 ) are considered only in
the resistor–less version (Fig. 3.7b). Equation (3.12) shows that sensitivities of the
oscillation frequency on parameters of active elements (current gain 𝐵) are quite
1.0V
1.0V
0V
0V
-1.0V
73.70us
74.00us
V(out1)
V(out2)
74.40us
74.80us
75.20us
75.60us
Time
-1.0V
Fig. 3.9: 7Time
waveforms
of the
output signals
(for 𝑉7 5𝑆𝐸𝑇
= 2 7𝑉5 . 6,0 u𝑉s 𝑆𝐸𝑇 _𝐵 = 0 𝑉 ),
3.70us
74.00us
74.40us
74.80us
. 2 0 u s _𝐴
V(out1)
V(out2)
me
given by simulation (transient analysis inT iPSpice).
-0
-20
-40
-60
0Hz
2MHz
4MHz
Vdb(out1)
Vdb(out2)
6MHz
8MHz
10MHz
12MHz
Frequency
Fig. 3.10: Spectrum of the output signals.
40
14MHz
16MHz
high for 𝐵1 𝐵2 −→ 1 (Fig. 3.8) or 𝐵2 −→ 0.5 whereas 𝐵1 = 2 respectively (see
section 3.2.2).
The values of the capacitors are chosen 𝐶1 = 𝐶2 = 470 𝑝𝐹 , and the external
resistors 𝑅1𝑒𝑥𝑡 = 𝑅2𝑒𝑥𝑡 = 100 Ω. Considering the virtual resistances 𝑅𝑥 = 95 Ω the
total values result in 𝑅1 = 𝑅2 = 195 Ω. The current gain 𝐵1 is chosen 𝐵1 = 2 (then
𝑉𝑆𝐸𝑇 _𝐴 ≈ 2 𝑉 ) and 𝐵2 will be changed taking into account the oscillation condition
and limited range of control by 𝐵 above. The expected value of the oscillation
frequency estimated by (3.9) is 𝑓0 = 1.737 𝑀 𝐻𝑧 (𝐵2 = 0).
3.2.2
Simulation and Measurement Results
-0
To verify the
proposed oscillator the simulations in PSpice using an adequate model
of the real CCII– have been carried out. Fig. 3.9 shows the time waveforms of the
output signals in both nodes denoted in circuit diagram (Fig. 3.7). Spectrum of the
-20
output signal
resulting from the simulation using PSpice is given in Fig. 3.10. The
simulations were supplemented by adequate laboratory measurements, as shown in
Fig. 3.11 and Fig. 3.12. These results are confirmation of the theoretical and design
- 4 0 and also symbolic analysis given above. For start of the oscillations it
assumptions
was necessary to change the value of the 𝑅1 to 67 Ω, which caused changing of the
expected theoretical value of the oscillation frequency (𝑓0 ) to 1.9 𝑀 𝐻𝑧 (instead of
1.7 𝑀 𝐻𝑧).- 6 0The parasitic properties of active elements (𝑅𝑥 and their different values
given by manufacturing
tolerance)
causes
that
condition
of 1oscillation
is not
fulfilled.
0Hz
2MHz
4MHz
6MHz
8MHz
10MHz
2MHz
14MHz
16MHz
Vdb(out1)
Vdb(out2)
Frequency
Fig. 3.11: Measured output signals (larger is 𝑉𝑂𝑈 𝑇 1 , smaller is 𝑉𝑂𝑈 𝑇 2 for 𝑉𝑆𝐸𝑇 _𝐴 =
2 𝑉 , 𝑉𝑆𝐸𝑇 _𝐵 = 0 𝑉 ).Horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣.
41
Fig. 3.12: Measured spectrum of the output signal.
Although the influence of parasitic real features is discussed in the next section in
detail, let’s mention, that with regard to the parasitic features of the active blocks,
the oscillation frequency is changed to 1.8 𝑀 𝐻𝑧, which was confirmed with the
simulation by the macro models from [193]. The value of the 𝑓0 measured in laboratory was still about 50 𝑘𝐻𝑧 lower (1.75 𝑀 𝐻𝑧). The dependence of the oscillation
frequency 𝑓0 on the control voltage 𝑉𝑆𝐸𝑇 _𝐴 is shown in Fig. 3.13, namely ideal theoretical, PSpice simulation, Matlab calculation and measured too. The measurement
of the output voltages (𝑉𝑂𝑈 𝑇 1 and 𝑉𝑂𝑈 𝑇 2 ) versus the oscillation frequency (𝑓0 ) is
f 0 2,0
[MHz]
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,1
0,2
0,3
ideal (theoretical)
PSpice simulation
0,4
V SET_A [V]
0,5
Matlab calculation
Measurement
Fig. 3.13: Oscillation frequency versus control voltage.
42
V out1,2 [Vp-p]
2
1,8
V OUT1
1,6
1,4
1,2
1
V OUT2
0,8
0,6
0,4
0,2
0
0,0
0,5
1,0
1,5
f 0 [MHz]
2,0
Fig. 3.14: Output voltages vs. oscillation frequency (measured).
shown in the Fig. 3.14. Similarly, the measurement of dependence of the THD on
the oscillation frequency 𝑓0 is given in Fig. 3.15.
The maximal tunable frequency range is from 0.32 to 1.75 𝑀 𝐻𝑧 (𝑉𝑆𝐸𝑇 _𝐵 from
0 to 0.48 𝑉 ). Nevertheless, we can see (Fig. 3.14 and Fig. 3.15) that for the minimal
THD it is acceptable to work with the control voltage 𝑉𝑆𝐸𝑇 _𝐵 from 0 to about 0.3 𝑉
(THD is below 1%). It reduces tuning to half range (approximately from 1 𝑀 𝐻𝑧
to 1.75 𝑀 𝐻𝑧). There lower THD was achieved due to the internal nonlinearity of
used active elements. In a wider range, it is necessary to add a circuit for amplitude
stabilization. The first approach contained CC1 with a fixed gain. Practically, in
THD 10
[%] 9
8
7
6
5
4
3
2
1
0
0,0
0,5
1,0
1,5
f 0 [Hz]
2,0
Fig. 3.15: THD versus oscillation frequency (measured).
43
this case we can obtain an invariable output level in the total range of 𝑓0 but
THD is incredible and output waveform even limited. The CC1 with an adjustable
gain is better for direct controlling of the condition of oscillation but it affects a
little bit also oscillation frequency (3.9) and output magnitude. It is appropriate for
external amplitude stabilization. For keeping output amplitudes in less invariable
level (Fig. 3.14) it was necessary to set 𝑉𝑆𝐸𝑇 _𝐴 in every measured point (only very
small change), but THD increased when 𝑉𝑆𝐸𝑇 _𝐵 was above 0.3 𝑉 . In other case
(𝑉𝑆𝐸𝑇 _𝐴 was fixed) the amplitudes varied for example from 0.5 to 1 𝑉𝑝−𝑝 (𝑉𝑂𝑈 𝑇 2 )
but THD was still under 1%. In the rest of theoretical range (approximately from
0.35 to 0.5 𝑉 ) it is important to set 𝑉𝑆𝐸𝑇 _𝐴 in each next measured point otherwise
THD is very high.
3.2.3
Parasitic Influences
In Fig. 3.16 the suitable model of the real CCII– which includes the most important
parasitic parameters is given. Then using this model (Fig. 3.16) the circuit diagram
VSET
1
Y
2 pF
Cy
Ry
Z
Cz
2 MΩ
Ix
Rz
Rx
X
Fig. 3.16: Important parasitic influences of CCII–
from Fig. 3.7 can be supplemented as shown
Gp Cp in Fig. 3.17 to include all parasitic
OUT2
Rs1
VSET_B
CC2
VSET_A
CC1
C2
X
C1
CCII- Z
Y
Y
Rs2
CCII- Z
X
OUT1
Yp2
Yp1
Fig. 3.17: Important parasitic influences in the proposed oscillator.
44
influences of the practical oscillator. Elements with crosshatch pattern are representing parasitic influences. This circuit (Fig. 3.17) has the characteristic equation in
the polynomial form (3.5) with the coefficients in symbolical form as follows:
𝑎2 = 1,
𝑎1 =
(3.13)
𝐶1 𝐺𝑠2 +𝐺𝑠1 𝐶𝑝1 +𝐶2 𝐺𝑝1
+
𝐶𝑝1 𝐶1 +𝐶𝑝1 𝐶2 +𝐶𝑝2 𝐶2 +𝐶𝑝1 𝐶𝑝2 +𝐶1 𝐶2
𝐺 𝐵*𝐶
+𝐺
𝐶
+𝐺 𝐶
𝑠2 2 𝑝1
𝑝2 𝑝1
𝑠2 𝑝2
+ 𝐶𝑝1 𝐶1 +𝐶
+
𝑝1 𝐶2 +𝐶𝑝2 𝐶2 +𝐶𝑝1 𝐶𝑝2 +𝐶1 𝐶2
+
𝑎0 =
𝐶1 𝐺𝑝1 +𝐶2 𝐺𝑠1 −𝐵1* 𝐶2 𝐺𝑠1 +𝐶𝑝2 𝐺𝑝1 +𝐶𝑝2 𝐶2
𝐶𝑝1 𝐶1 +𝐶𝑝1 𝐶2 +𝐶𝑝2 𝐶2 +𝐶𝑝1 𝐶𝑝2 +𝐶1 𝐶2
,
(1−𝐵1* 𝐵2* )𝐺𝑠1 𝐺𝑠2 +𝐺𝑝1 𝐺𝑝2 +𝐺𝑠1 𝐺𝑝1 +𝐺𝑠2 𝐺𝑝2 +𝐺𝑠2 𝐺𝑝1 𝐵2*
𝐶𝑝1 𝐶1 +𝐶𝑝1 𝐶2 +𝐶𝑝2 𝐶2 +𝐶𝑝1 𝐶𝑝2 +𝐶1 𝐶2
(3.14)
.
(3.15)
In formulas (3.14) and (3.15) the following symbols represent the parasitic influences:
𝑅𝑠1 =
𝑅𝑠2 =
1
= 𝑅1𝑒𝑥𝑡 + 𝑅𝑥1 ± Δ𝑅𝑥1 = 𝑅1𝑒𝑥𝑡 + 95 ± 20% Ω,
𝐺𝑠1
1
= 𝑅2𝑒𝑥𝑡 + 𝑅𝑥2 ± Δ𝑅𝑥2 = 𝑅2𝑒𝑥𝑡 + 95 ± 20% Ω,
𝐺𝑠2
1
𝐺𝑝1 =
,
𝑅𝑧1
1
1
+
,
𝐺𝑝2 =
𝑅𝑧2 𝑅𝑦2
(3.16)
(3.17)
(3.18)
(3.19)
𝐶𝑝1 = 𝐶𝑧1 ,
(3.20)
𝐶𝑝2 = 𝐶𝑧2 + 𝐶𝑦2 ,
(3.21)
𝐵1 𝜔𝑇
,
(3.22)
𝑠 + 𝜔𝑇
𝐵2 𝜔𝑇
.
(3.23)
𝐵2* =
𝑠 + 𝜔𝑇
Analyzing the equations above, one can see that the influence of the resistance 𝑅𝑝 =
1/𝐺𝑝 begins to show symptom in slight increasing of the oscillation frequency 𝑓0 for
𝑅𝑝 less than 50 𝑘Ω (but the employed blocks allow to achieve several higher values).
Note that the influence of the 𝑅𝑝1 is only slightly larger than 𝑅𝑝2 . On the other hand
the capacitances 𝐶𝑝 play more significant role. Only small change of the capacitance
results in a significant change of 𝑓0 (e.g. for both 𝐶𝑝 = 5 𝑝𝐹 it is over 20 𝑘𝐻𝑧).
The influence of the 𝐶𝑝2 is greater than 𝐶𝑝1 due to their values, approximately
𝐶𝑝1 = 5 𝑝𝐹 and 𝐶𝑝2 = 7 𝑝𝐹 . This is due to the fact that the parasitic capacitance
𝐶𝑦 plays also role but not in 𝐶𝐶1 (port 𝑌 is grounded). Furthermore inequality
of the input resistances of the current ports 𝑅𝑥1 ̸= 𝑅𝑥2 plays a significant role,
too. Their values are determined by technology and have high production tolerance.
𝐵1* =
45
The results obtained by direct analysis of the model (Fig. 3.17) respecting essential
parasitic influences in the real oscillator are in a very good accordance with the
computer simulations and obtained experimental results. Due to the relatively high
tolerance of the resistances 𝑅𝑥 , the difference between the theoretically assumed
value and the measurement is greater than the difference between the computer
simulation and the direct analysis of the model above.
46
3.3
Study of 3R–2C Oscillator
Oscillator conceptions that are focused mainly on direct electronic control are presented. During circuit design are important these features: a) all capacitors are grounded
(required for on-chip implementation); b) active elements with single current input
and single voltage output are sufficient; c) only two active elements are required;
d) independent control of oscillation frequency and condition of oscillations without
mutual disturbance; e) 𝑓0 and CO controlled without changes of any passive element;
f) buffered outputs - no additional buffering is necessary; g) simple implementation
of amplitude (automatic) gain control (AGC) for 𝑓0 adjusting and satisfying total
harmonic distortion (THD) - only rectified output voltage is required; h) real parts
of current input (intrinsic) impedance of active elements are absorbed to values of
working (external) resistors. Above discussed solutions were the most important for
our approach although many others were presented in literature. Current gain based
approaches have not been frequently used for control the oscillators. It is clear that
some of discussed solutions use less number of active elements, but direct frequency
control and other advantages discussed bellow are not simultaneously allowed. Last
research was focused also on current-mode solutions (high-impedance outputs, for
example [12]). Solutions providing voltage (low-impedance) outputs are discussed
in this paper. Necessity of additional voltage buffers or current to voltage converters for voltage-mode operation is the most important problem of some previous
works. Some hitherto published realizations are really economical (minimal number
of active elements), but characteristic equation is not suitable for electronic control,
active elements are quite complicated (many inputs and outputs) many of them do
not provide quadrature outputs and in the most cases relation between produced
amplitudes and total harmonic distortion in dependence on 𝑓0 adjusting are not
mentioned or investigated. Three modified oscillator conceptions that are quite simple, directly electronically adjustable, providing independent control of oscillation
condition and frequency were designed. Positive and negative aspects of presented
method of control are discussed. Expected assumptions of adjustability are verified
experimentally on one of the presented solution.
3.3.1
Proposed Oscillators
In this case we have used well–know and popular method for synthesis and design of
oscillators. Approach is based on lossless and lossy integrators in the loop. Approach
using state variable methods [119, 44, 42, 43, 137] could also be used for this synthesis
and results will be identical. The first designed circuit is shown in Fig. 3.18 and is
47
VSET2
VSET2
COcontro l
OUT2
R1
2
w CG-CFBA p
z
z
VSET1
VSET1
R3
f0 control
OUT1
R2
OUT1
1
2
n CG-CIBA w
z
z
1
R2
2
1
C2
C1
C2
Fig. 3.18: The first proposed oscillator.
described by the following characteristic equation:
−𝐺1 − 𝐺2 − 𝐺3 + 𝐺3 𝐵2
𝐵1 𝐺1 𝐺2
𝑠+
= 0.
𝐶2
𝐶1 𝐶2
(3.24)
Condition of oscillation and oscillation frequency are:
𝐵2 = 1 +
√︃
𝜔0 =
𝐺1 + 𝐺2
,
𝐺3
𝐵1 𝐺1 𝐺2
,
𝐶1 𝐶2
(3.25)
(3.26)
where adjustable current gain 𝐵1 stands for current gain of first active element (CGCIBA) and 𝐵2 represents current gain of the second active element (CG-CFBA).
Second solution of the oscillator shown in Fig. 3.19 was derived from the circuit in
Fig. 3.18 when the resistor 𝑅1 is directly connected to the voltage output of the CGCFBA. This modification of the oscillator has positive effect on the characteristic
equation, which has now the following form:
𝑠2 +
R3
f0 control
n CG-CIBA w
C1
𝑠2 +
2
w CG-CFBA p
R1
1
COcontro l
OUT2
−𝐺2 − 𝐺3 + 𝐺3 𝐵2
𝐵1 𝐺1 𝐺2
𝑠+
= 0.
𝐶2
𝐶1 𝐶2
(3.27)
Oscillation frequency has same form as in (3.26), but condition of oscillation is now:
𝐵2 = 1 +
𝐺2
.
𝐺3
(3.28)
As shown later, we suppose equality of passive elements for further simplification:
𝑅1 = 𝑅2 = 𝑅 and 𝐶1 = 𝐶2 = 𝐶. We used discussed simplifications and compared
CO (3.25) and (3.28). Theoretical gains 𝐵2 = 3 (Fig. 3.18) and 𝐵2 = 2 (Fig. 3.19)
48
VSET2
COcontro l
R1
2
OUT2
R1
f0 contro l
VSET2
COcontro l
OUT2
COcontro l
VSET_B2
VSET_A2
2
w CG-CFBA p
w CG-CFBA p
z
z
R1
2
n CG-ICVA w
z
VSET1
R3
f0 control
1
OUT1
VSET1
R2
R3
f0 control
OUT1
1
2
VSET1
R2
1
2
n CG-CIBA w
n CG-CIBA w
n CG-CIBA w
z
z
z
1
C1
1
C2
R3
OUT1
R2
2
1
C1
C2
C1
C2
Fig. 3.19: The second version of the oscillator.
are required to start the oscillations. Control of 𝑓0 by only one parameter (𝐵1 )
without another matching condition is advantageous. We are interested only in direct
electronic control. Therefore, tuning by passive element is not appropriate for our
approach. The ideal relative sensitivities of 𝑓0 on circuit parameters are
1
𝑆𝐵𝜔01 = −𝑆𝑅𝜔01 = −𝑆𝑅𝜔02 = −𝑆𝐶𝜔01 = −𝑆𝐶𝜔02 = ,
2
(3.29)
𝑆𝐵𝜔02 = 𝑆𝑅𝜔03 = 0.
(3.30)
The ratio between amplitude of state voltages 𝑣1 and 𝑣2 (therefore also between
𝑉𝑂𝑈 𝑇 1 and 𝑉𝑂𝑈 𝑇 2 ) is
−𝐵1
−𝐵1
𝑉𝑂𝑈 𝑇 1
=
=
.
(3.31)
𝑉𝑂𝑈 𝑇 2
𝑠𝑅1 𝐶1
𝑗𝜔𝑅1 𝐶1
Substitution of the 𝜔 by 𝜔0 from (3.26) to (3.31) leads to
√︃
𝑉𝑂𝑈 𝑇 1
−𝐵1
𝑅2 𝐶2
= √︁ 𝐵
= −𝑗𝐵1
.
𝑉𝑂𝑈 𝑇 2
𝑅1 𝐶1 𝐵1
𝑗 𝑅1 𝑅2 𝐶1 1 𝐶2 𝑅1 𝐶1
(3.32)
It confirms the fact that the both produced signals are in quadrature. If we suppose
equality 𝑅1 = 𝑅2 = 𝑅 and 𝐶1 = 𝐶2 = 𝐶 then relation between both voltages is
given by
√︁
𝑉𝑂𝑈 𝑇 1
= −𝑗 𝐵1 ,
(3.33)
𝑉𝑂𝑈 𝑇 2
therefore amplitude of 𝑉𝑂𝑈 𝑇 1 is dependent on 𝐵1 and in fact on adjusted 𝑓0 . Produced signals have equal amplitudes for 𝐵1 = 1. This problem is not often discussed
and studied in detail, but it is usually presented in many hitherto published simple
oscillator solutions (for example [46, 152]). Nonlinear dependence of 𝑓0 on parameter
𝐵1 (suitable for tuning) is next consequence.
49
f0 contro l
VSET2
COcontro l
R1
OUT2
COcontro l
VSET_B2
VSET_A2
2
w CG-CFBA p
R1
2
z
n CG-ICVA w
z
VSET1
R3
f0 control
1
OUT1
VSET1
R2
1
2
n CG-CIBA w
R2
2
n CG-CIBA w
z
z
1
C1
R3
OUT1
1
C2
C1
C2
Fig. 3.20: Third version of oscillator with direct electronic adjusting.
We also proposed a solution where dependence of produced amplitudes on tuning
process is eliminated and tuning characteristic is linear. However, necessity of matching
of two gains is now important [14]. The third oscillator (Fig. 3.20) is described by
the following characteristic equation:
𝑠2 +
𝐺1 + 𝐺3 − 𝐺3 𝐴2
𝐵1 𝐵2 𝐺1 𝐺2
𝑠+
.
𝐶2
𝐶1 𝐶2
(3.34)
The CO and 𝑓0 determined from (3.34) have forms:
𝐴2 = 1 +
𝐺1
,
𝐺3
(3.35)
√︃
𝐵1 𝐵2 𝐺1 𝐺2
.
(3.36)
𝐶1 𝐶2
The parameter 𝐴2 is the voltage gain of the CG-ICVA in Fig. 3.20. For more details
see principle in Fig. 3.5. Relation between produced amplitudes is
𝜔0 =
𝑉𝑂𝑈 𝑇 1
𝐵1
𝐵1
=
=
,
𝑉𝑂𝑈 𝑇 2
𝑠𝑅1 𝐶1
𝑗𝜔𝑅1 𝐶1
(3.37)
and after modification it leads to
√︃
𝑉𝑂𝑈 𝑇 1
𝐵1
𝑅2 𝐶2
= √︁ 𝐵 𝐵
= −𝑗𝐵1
.
𝑉𝑂𝑈 𝑇 2
𝑅1 𝐶1 𝐵1 𝐵2
𝑗 𝑅1 𝑅12 𝐶12 𝐶2 𝑅1 𝐶1
(3.38)
We suppose 𝐵1 = 𝐵2 = 𝐵 and therefore (3.38) simplifies to
√︃
𝑉𝑂𝑈 𝑇 1
𝑅2 𝐶2
= −𝑗
.
𝑉𝑂𝑈 𝑇 2
𝑅1 𝐶1
(3.39)
We also suppose above discussed simplification of equality of passive elements. Therefore output amplitudes are equal to each other even if 𝑓0 is tuned.
50
The ideal relative sensitivities of 𝑓0 in (3.36) on circuit parameters are very
similar to the previous case:
1
𝑆𝐵𝜔01 = 𝑆𝐵𝜔02 = −𝑆𝑅𝜔01 = −𝑆𝑅𝜔02 = −𝑆𝐶𝜔01 = −𝑆𝐶𝜔02 = ,
2
(3.40)
𝑆𝐴𝜔02 = 𝑆𝑅𝜔03 = 0.
(3.41)
Implementation of adjustable current gain is very favorable for direct electronically controllable applications, for example oscillators. For instance, both circuits
in [16] allow tuning by changing the values of resistors only. For example, second
circuit in [16] does not allow tuning without changes of one amplitude as discussed
by authors in [16]. Changing the value of only one resistor is suitable for 𝑓0 tuning.
However, this approach [14] allows to control 𝑓0 similarly as it is shown in Fig. 3.20
(𝐵1 and 𝐵2 for tuning of 𝑓0 ).
3.3.2
Simulation and Measurement Results
The second solution of the oscillator (Fig. 3.19) was chosen as an example for experimental verification and detailed analysis. Knowledge of expected behavior and
influences of real active elements is necessary for practical utilization of proposed
circuit in complex communication systems. We can neglect some parameters (for
example output resistance of 𝑤 and 𝑏 - there are very low values below 1 Ω) because
their effect on function is insignificant. However, influences of real parameters of 𝑝
and 𝑧 terminals are very important and they affect at least oscillation frequency
(small or large shift) and oscillation condition. Behavior of each circuit is affected
by real features of active elements. Input resistance (port 𝑝 or 𝑛) of both active elements is labeled as 𝑅𝑝 or 𝑅𝑛 . Output resistances 𝑅𝑤 (at port 𝑤) are in most cases
negligible because opamp (as voltage buffer) has values < 1 Ω in wide frequency
range. Input capacitances of active elements have minimal impact because they are
p
B.Ip
p
Rp
Ip
B.Ip
Rp
Ip
R
Rn
B.In
n
In
1
w
In
R
z
z
Cz
Cz
Cz
CG-CFBA
B.In
Rn
1
R
z
Cz
z
w n
R
z
CG-CFBA
1
w
1
VSET
VSET
VSET
VSET
CG-CIBA
z
(a)
z
CG-CIBA
z
(b)
Fig. 3.21: Non-ideal models of used active elements: a) CG-CFBA, b) CG-CIBA.
51
w
C1
C2
C1
C2
VSET
1
Ip
p
R
z
w-
Rp
p
w-
R
B.Ip
VSET_A
A
R
Cz
z
Rp
B.Ip
Vb = Vz
I
b p
Cz
CG-CFDOBA
z
CG-BCVA
z
(a)
f0 control
Vw = Vz.A
w
1
C2
VSET_B
p
Ip
z
Cz
CG-CFDOBA
w+
1
Ip
Cz
z
p
C1
VSET_A
R
B.Ip
w+R
1
C2
VSET_B
VSET
B.Ip
Rp
C1
CG-BCVA
z
A
Vw
w
1
Vb
b
z
(b)
AGC INP
f0 control
CO control
CO controlVDD RP
AGC INP
VSS
V
RP
V
DD
SS
Fig.
3.22: Non-ideal models
ofVused
active elements: a) CG-CFDOBA,
b) CG-BCVA.
VSET_A2
VSET_B2
VSET_B2
SET_A2
Rf
100 kΩ
R2'
2
OUT3 R2'
w
2
1
w-
CG-CFDOBA p
w+
z
Z1
1
C1
Rf
R3
220 Ω 100 kΩ
b
Cf
OUTquite
Cf
together
with
small
of auxiliary
port 𝑧 consistR5of high
2
z
VSET_B1
C1
C1
1 mF R2
resistive
node 11 uF
and 1node
2 2are influenced1 uF
by
mF R
R and capacitive part. High
R3 impedance
1 kΩ
R1' OUT2 3 w- 1
R
'
1
1i
2
output resistance
of used current amplifier and by input resistance
R4 of voltage buffer.
CG-CFDOBA p
R4
100 kΩ
100
kΩ
TL072
TL072
w+
R
OUT1labeled this
R 𝑅 . Capacitances in auxiliary port are labeled as 𝐶 .
We
parameter
as
z
𝑧
𝑧
1/2
1/2
R
AGC1OUT
1 kΩ
TL072
C
kΩ
C 2x BAT42
2x
BAT42
1 of used
Basic models
active elements for non-ideal analysis are in Fig. 3.21,
resp
2/2
C
C2
C2
Fig. 3.22.C1CG-CIBA was
built from four quadrant current-mode multiplier EL4083
[194] (it allows both negative and positive current output). However, current gain
adjusting is limited only to unity [194]. Second part (voltage buffer) was constructed
by dual opamp LT1364 [195]. CG-CFBA was created from current-mode multiplier
EL2082 [193] because it allows larger range of current gain. Opamp LT1364 was also
used. In our case is 𝑅𝑧 ≈ 830 kΩ. Output impedances of EL4083 and EL2082 are
approximately 1 MΩ/ 5 pF and input impedance of LT1364 is approximately 5 MΩ/
3 pF [195]. Both parasitic capacitances have approximately values 𝐶𝑧 ≈ 8 pF. Input
Z2
Z1
z2
Cz1
100 kΩ
R1
3
p CG-BCVA
Z2
R
R
OUT3
220 Ω 100 kΩ
b
resistance.
Impedances
OUT2
z
p CG-BCVA
VSET_B1
R1
w
z2
z1
VSET2
OUT2
R1
2
w CG-CFBA p
z
R3
VSET1
OUT1 R
2
1
2
n CG-CIBA w
z
Cz1
Rz1
1
Rz2
C1
Cz2
C2
Fig. 3.23: Important parasitic influences in the circuit of the second oscillator.
52
resistance of inverting CG-CIBA (𝑅𝑛 ) is dependent on auxiliary bias current and
varies in range from 40 to 700 Ω if auxiliary bias current is changed from 2.5 mA to
0.2 mA [97]. It was tested experimentally, because it is not discussed in [194]. Expected value of 𝑅𝑛 is approximately 300 Ω in our case (it is quite high value). Input
resistance of CG-CFBA has fixed and lower value, 𝑅𝑝 ≈ 95 Ω. Passive external elements of oscillator (Fig. 3.19) were selected as 𝑅1 = 𝑅2 = 𝑅3 = 1kΩ, 𝐶1 = 𝐶2 = 100
pF and parameters of active elements were designed as 𝐵1 = 1, 𝐵2 = 2, respectively.
The model of oscillator in Fig. 3.23 takes into account also important parasitic elements placed in critical parts of the circuit (𝑅𝑧1 = 𝑅𝑧2 = 830 kΩ, 𝐶𝑧1 = 𝐶𝑧2 = 8
pF). Real values of passive elements are 𝑅1′ = 𝑅1 + 𝑅𝑛 ≈ 1.3 kΩ, 𝑅3′ = 𝑅3 + 𝑅𝑝 ≈
1.1 kΩ, 𝐶1′ = 𝐶1 + 𝐶𝑧1 ≈ 108 pF, 𝐶2 ≈ 108 pF. CO and 𝑓0 have now following and
more complex forms:
𝐵2′ ≥
𝜔0′ =
𝑅1′ 𝑅𝑧1 𝑅𝑧2 𝐶1′ (𝑅2 + 𝑅3′ ) + 𝑅1′ 𝑅2 𝑅3′ (𝑅𝑧1 𝐶1′ + 𝑅𝑧2 𝐶2′ )
,
𝑅1′ 𝑅2 𝑅𝑧1 𝑅𝑧2 𝐶1′
⎯
⎸ ′
⎸ 𝑅3 𝑅𝑧2 (𝐵1 𝑅𝑧1
⎷
+ 𝑅1′ ) + 𝑅1′ 𝑅2 (𝑅𝑧2 − 𝐵2 𝑅𝑧2 + 𝑅3′ )
.
𝑅1′ 𝑅2 𝑅3′ 𝑅𝑧1 𝑅𝑧2 𝐶1′ 𝐶2′
(3.42)
(3.43)
From (3.43) it is clear that 𝐵2 could influence oscillation frequency. Nevertheless,
impact of second sum term in (3.43) is very small because has several times lower
value in comparison with first term and 𝐵2 has quite constant value (in comparison
to 𝐵1 ). Possible influence on exact value of 𝑓0 appears for 𝐵1 < 0.1 only. Influences
P1
AGC
10 k
Cf
1m
Rh
Q1
2.2 k
Vh
VSET2
CO control
R1
2
w CG-CFBA p
OUT2
z
f0 control
R3
VSET1
1
OUT1 R
2
p CG-CIBA w
z
C1
C2
Fig. 3.24: Second version of the oscillator with AGC.
53
Fig. 3.25: Measured results - transient responses. Horizontal axis 200𝑛𝑠/𝑑𝑖𝑣, vertical
axis 500 𝑚𝑉 /𝑑𝑖𝑣.
Fig. 3.26: Measured results - spectrum of 𝑉𝑂𝑈 𝑇 2 .
of imperfections of voltage followers were also found in 𝑓0 . Modified equation (3.43),
considering these problems is in form:
𝜔0′ =
⎯
⎸ ′
⎸ 𝑅3 𝑅𝑧2 (𝐵1 𝑅𝑧1 𝛼1 𝛼2
⎷
+ 𝑅1′ ) + 𝑅1′ 𝑅2 (𝑅𝑧2 − 𝐵2 𝑅𝑧2 + 𝑅3′ )
,
𝑅1′ 𝑅2 𝑅3′ 𝑅𝑧1 𝑅𝑧2 𝐶1′ 𝐶2′
54
(3.44)
where 𝛼1 and 𝛼2 are non–ideal voltage gains. Practically, these gains are not equal
to 1. The circuit was complemented by AGC system (Fig. 3.24) employing simple common–source transistor stage, which allows control of 𝐵2 through 𝑉𝑆𝐸𝑇 2 by
rectified output signal. Common bipolar transistor BC547B and diode 1N4148 was
used in AGC. Voltage 𝑉ℎ in ACG circuit is derived from voltage setting the CO
Fig. 3.27: Results of tuning process - dependence of THD on oscillation frequency
𝑓0 .
Fig. 3.28: Dependence of 𝑓0 on controlled current gain 𝐵1 .
55
and value is between 2 - 2.5 V. Increasing of output level causes larger base-emitter
voltage and causes decreasing of 𝑉𝑆𝐸𝑇 2 (therefore also 𝐵2 ). Decreasing of 𝑉𝑂𝑈 𝑇 2
causes increasing of 𝑉𝑆𝐸𝑇 2 . A very precise and careful setting is necessary for correct
operation of AGC. Results of experiments were obtained by oscilloscope Agilent Infinium 54820A and vector network/spectrum analyzer Agilent 4395A. Supply voltage
Fig. 3.29: Results of tuning process - dependence of output levels on oscillation
frequency 𝑓0 .
Fig. 3.30: Dependence of 𝑉𝑂𝑈 𝑇 1 on controlled current gain 𝐵1 .
56
was 𝑉𝐷𝐷 = 5 𝑉 and 𝑉𝑆𝑆 = −5 𝑉 . Real active elements and their properties are considered. Expected oscillation frequency is 𝑓0 = 1.293 𝑀 𝐻𝑧 (3.43) for selected and
designed parameters (if 𝐵1 = 1). Measured value was 1.257𝑀 𝐻𝑧. Deviation is mostly
caused by inaccuracy of expected value of 𝑅𝑛1 . This parameter is also dependent on
bias current [194]. Transient response is shown in Fig. 3.25 and spectrum of 𝑉𝑂𝑈 𝑇 2 in
Fig. 3.26. Relation between control voltages and current gains are 𝐵1 ≈ 𝑉𝑆𝐸𝑇 1 /𝑉𝐷𝐷
[194] and 𝐵2 ≈ 𝑉𝑆𝐸𝑇 2 [193]. Attenuation of higher harmonic components is greater
than 40 𝑑𝐵 (Fig. 3.26) and THD is in range from 0.6 to 1 (Fig. 3.27). Range of
tunability was measured from 100 𝑘𝐻𝑧 to 1.257 𝑀 𝐻𝑧 for 𝐵1 changed from 0.01 to
1, see Fig. 3.28. Output level (𝑉𝑂𝑈 𝑇 2 ) has quite constant value 2.22 ± 0.06 𝑉𝑃 −𝑃
in frequency range between 400 𝑘𝐻𝑧 and 1.257 𝑀 𝐻𝑧 (𝐵1 ∈ {0.1; 1}), see Fig. 3.29.
THD of 𝑉𝑂𝑈 𝑇 1 is about 1 - 1.3 in almost whole range of 𝑓0 adjusting (Fig. 3.27).
Output level of 𝑉𝑂𝑈 𝑇 1 changes according to 𝐵1 from 0.22 𝑉 to 2.24 𝑉 , see Fig. 3.29.
Dependence of 𝑉𝑂𝑈 𝑇 1 on 𝐵1 is depicted in Fig. 3.30. It confirms eq. (3.33) very well.
57
3.4
Multiphase Oscillator Based on CG–BCVA
A new oscillator suitable for quadrature and multiphase signal generation is introduced in this contribution. Novel active element, so–called controlled gain–buffered
current and voltage amplifier (CG-BCVA) with electronic possibilities of current
and voltage gain adjusting is implemented together with controlled gain–current
follower differential output buffered amplifier (CG-CFDOBA) for linear adjusting of
oscillation frequency and precise control of oscillation condition in order to ensure
stable level of generated voltages and sufficient total harmonic distortion. To the best
of authors knowledge none similar active element (CG-BCVA) and its application
in oscillators with controllable features has not been reported in open literature
yet. Parameters of the oscillator are directly controllable electronically. Simultaneous changes of two current gains allow linear adjusting of oscillation frequency and
controllable voltage gain is intended to control the oscillation condition. Detailed
comparison of discussed circuits with recently developed and discovered solutions
employing the same type of electronic control was provided and shows useful features of proposed oscillator and utilized methods of electronic control. Behavioral
models based on commercially available ICs were used for experimental purposes.
Laboratory experiments confirmed the workability and estimated behavior of the
proposed circuit as well.
3.4.1
Proposed Oscillators
We used above discussed active elements for design of precise adjustable oscillator
with multiphase output properties. Proposed circuit and its modification are shown
in Fig. 3.31, resp. Fig. 3.32. Theory of used synthesis principle is the following: we
f0 control
f0 cont
CO control
VSET_B2 VSET_A2
R2
2
w
OUT3
b
OUT2
p CG-BCVA
VSET_B1
OUT1i
w-
OUT1
w+
z
R1
1
VSET_B1
R3
2
CG-CFDOBA p
z
OUT1i
w-
OUT1
w+
z
1
C1
1
CG-CFDOBA p
1
C2
C1
Fig. 3.31: Basic solution of tunable multiphase oscillator employing two active elements based on controlled gains.
VSET_B
VSET
p
Rp
Ip
58p
B.I
1
R
z
Cz
R
z
w+
w-
p
Rp
Ip
B
put two integrators (lossy and lossless) in closed loop, where one integrator was
complemented by negative resistance. We created this part by adjustable voltage
amplifier in frame of CG-BCVA and resistor 𝑅3 . Characteristic equation has the
following form:
𝐵1 𝐵2
𝑅1 + 𝑅3 − 𝑅1 𝐴2
𝑠+
= 0.
(3.45)
𝑠2 +
𝑅1 𝑅3 𝐶2
𝑅1 𝑅2 𝐶1 𝐶2
Condition of oscillation and frequency of oscillation are:
√︃
𝜔0 =
(3.46)
𝐵1 𝐵2
.
𝑅1 𝑅2 𝐶1 𝐶2
(3.47)
Relative sensitivities of oscillation frequency (3.47) on values of passive elements
and current gains are theoretically equal to ±0.5. Analysis of relations between
generated signals (high-impedance nodes - voltage across capacitors) is provided as
follows:
√︃
𝑉𝑐1
𝐵1
𝐵1
𝑅2 𝐶2 𝐵1
=
=
= −𝑗
.
(3.48)
𝑉𝑐2
𝑠𝑅1 𝐶1
𝑗𝑅1 𝐶1
𝑅1 𝐶1 𝐵2
Considering equality of both current gains (𝐵1 = 𝐵2 = 𝐵1,2 ), eqs. (3.48) is simplified
as:
√︃
𝑅2 𝐶2
𝑉𝑐1
= −𝑗
.
(3.49)
𝑉𝑐2
𝑅1 𝐶1
Simultaneous change of current gains of both active elements, i.e. 𝐵1 = 𝐵2 = 𝐵1,2
(𝑉𝑆𝐸𝑇 _𝐵1 = 𝑉𝑆𝐸𝑇 _𝐵2 ) ensures linear control of 𝑓0 and voltage gain 𝐴2 (𝑉𝑆𝐸𝑇 _𝐴2 )
allows control of CO and amplitude stability from external precise (automatic) amplitude gain control circuit (AGC). In basic variant (Fig. 3.31), there are available
f0 control
CO control
CO control
VSET_B2 VSET_A2
2
VSET_B2 VSET_A2
OUT3
w
R2
p CG-BCVA
VSET_B1
z
R3
R1
2
OUT3
w
2
p CG-BCVA b-
OUT2
b
z
OUT1i
w-
OUT1
w+
R1
1
CG-CFDOBA p
OUT2i
OUT2
b+
R3
2
z
1
C2
C1
C2
Fig. 3.32: Modification solution of tunable multiphase oscillator employing two
active elements based on controlled gains for differential quadrature signal geneVSET_A
VSET_B
ration.
VSET
B.Ip
A
𝑅3
,
𝑅1
𝐴2 ≥ 1 +
1
R
z
R
z
w+
w-
p
Rp
Ip
Cz
CG-BCVA
B.Ip
Cz
A
Vw = Vz.A
w
1
Vb = Vz
b
59
four low-impedance voltage outputs. Output voltages 𝑉𝑂𝑈 𝑇 1 (terminal 𝑤+ of CGCFDOBA) and 𝑉𝑂𝑈 𝑇 2 (𝑏 terminal of CG-BCVA) have quadrature phase shift which
is consequence of (3.49). Output voltage 𝑉𝑂𝑈 𝑇 1𝑖 is available at the terminal 𝑤−
of CG-CFDOBA, which represents inversion of 𝑉𝑂𝑈 𝑇 1 . Generated voltage at the 𝑤
of CG-BCVA has same phase as 𝑉𝑂𝑈 𝑇 2 , only difference is caused by amplification
between 𝑤 and 𝑏 of CG-BCVA.
Solution in Fig. 3.31 produces three signals with phase shifts 90 and 180 degrees.
f0 control
f0 con
CO control generation or differential
Oscillator introduced in Fig. 3.32 is suitable for four-phase
V
V
quadrature signal generation because terminals (outputs of CG-BCVA) 𝑏+ (𝑉𝑂𝑈 𝑇 2 )
2
2
w
OUT3
and 𝑏− (𝑉𝑂𝑈 𝑇 2𝑖 ) are not influenced byRgain
𝐴p2CG-BCVA
(𝑉
𝑂𝑈 𝑇 3 ), which sets CO during the
b
OUT2
V
z
tuning process. Differential quadrature
signals are
available
at 𝑂𝑈 𝑇1 , 𝑂𝑈 𝑇1𝑖 and
V
R
3
𝑂𝑈 𝑇2 , 𝑂𝑈 𝑇2𝑖 in case of
Fig. 3.32.
SolutionRfrom
Fig. 3.31 is detailed analyzed in
1
1
wOUT1i
1
2
wOUT1i
CG-CFDOBA p
CG-CFDOBA
following sections. TheOUT
state variable
method of synthesis ([42, 43], for example)
w+
1
w+
OUT1
z
z
could also be used to obtain presented oscillator. However, such sophisticated me1
1
thods are not necessary for discussed
and quite
C1
C2 simple circuit. Integrators cascading
C1
and negative resistance are sufficient to complete proposed oscillator. Examples of
circuits derived by state variable methods were reported in impressive works written
by Gupta and Senani [42, 43]. Many oscillator structures including current feedback
amplifier (CFA) based integrators (in fact) in loops constructed by the state variVSET_B
able methods were introduced in both works
VSET[42, 43]. The oscillators in [43] utilize
simpler active elements (less number of outputs) than solution described in our
R
B.Ip
contribution. Unfortunately, solutions
reported
in [42, 43]
w+ belong to family of single
R
R
p
1
p
resistance controllable types, utilize
also high–impedance
w-voltage inputs (Y terminal
Ip
Ip
R
of CFA) and relations between amplitudes existC in case of tuning. Requirements for
both stable quadrature amplitudes while oscillator is tuned are demanded in many
CG-CFDOBA
CG-BCVA
z fulfills these specifications.
communication systems [14] and our solution
SET_A2
SET_B2
SET_B1
SET_B1
p
p
z
z
f0 control
CO control
AGC INP
VDD RP
VSS
VSET_B2 VSET_A2
100 kΩ
R2'
2
w
OUT3
b
OUT2
p CG-BCVA
VSET_B1
OUT1i
w-
OUT1
w+
z
R3
R1'
1
C1
C1
R2
100 kΩ
R
R
Z1
1
220 Ω 100 kΩ
1 mF
Z2
Cz2
Cz1
C2
Fig. 3.33: Model of proposed oscillator for non–ideal analysis.
60
Rf
R3
C
1
2
CG-CFDOBA p
z
R1
2x BAT42
TL072
1/2
3.4.2
Simulation and Measurement Results
We built behavioral model of both active elements for real laboratory experiments
from commercially available ICs in order to verify the functionality. Model of oscillator, where important influences are highlighted by hatched and small elements, is
shown in Fig. 3.33. We established behavioral model of CG-CFDOBA from current–
mode multiplier EL2082 [193] and differential voltage amplifier AD8138 [190] as
voltage buffer/inverter (full negative feedback). Parameters of CG-CFDOBA are
following: intrinsic resistance of current input terminal of current-mode multiplier 𝑝
is 𝑅𝑝1 ≈ 95Ω (EL2082 [193]), resistance of auxiliary high impedance terminal 𝑧 is
𝑅𝑧1 ≈ 860 𝑘Ω (output impedance of current–mode multiplier and input impedance
of voltage buffer: 1𝑀 Ω ‖ 6𝑀 Ω in parallel [190, 193]), capacitance of high-impedance
terminal z is 𝐶𝑧1 ≈ 6 𝑝𝐹 (capacitance of current output of EL2082 and input capacitance of AD8138 in parallel: 5 + 1 𝑝𝐹 [190, 193]). The real parameters of CG-BCVA
namely 𝑅𝑝2 are similar (𝑅𝑝2 ≈ 95 Ω) as in case of CG-CFDOBA (real behavioral
model utilizes also EL2082). We expect main difference at terminal 𝑧 where three
instead of two partial block (current amplifier, voltage amplifier and buffer) are interconnected. Estimated value of impedance in terminal 𝑧 is 𝑅𝑧2 ≈ 470 𝑘Ω (current
output resistance of EL2082, input resistance of adjustable voltage amplifier VCA810
[199] and input resistance of voltage buffer BUF634 [192]: 1𝑀 Ω ‖ 1 𝑀 Ω ‖ 8 𝑀 Ω),
𝐶𝑧2 ≈ 14𝑝𝐹 (output capacitance of EL2082, input capacitance of VCA810 and input
capacitance of BUF634: 5 + 1 + 8 𝑝𝐹 ).
Fig. 3.34: Transient responses at all available outputs (𝑉𝑂𝑈 𝑇 1 - blue color,
𝑉𝑂𝑈 𝑇 1𝑖 - green color, 𝑉𝑂𝑈 𝑇 2 - red color, 𝑉𝑂𝑈 𝑇 3 - orange color) for 𝐵1,2 = 1.1
(𝑉𝑓0 _𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 1.15 𝑉 ). Horizontal axis 50 𝑛𝑠/𝑑𝑖𝑣, vertical axis 50 𝑚𝑉 /𝑑𝑖𝑣.
61
Fig. 3.35: Transient responses at 𝑉𝑂𝑈 𝑇 1 and 𝑉𝑂𝑈 𝑇 2 for 𝐵1,2 =
(𝑉𝑓0 _𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 3.17 𝑉 ). Horizontal axis 20 𝑛𝑠/𝑑𝑖𝑣, vertical axis 50 𝑚𝑉 /𝑑𝑖𝑣.
2.9
We selected external passive elements as: 𝑅1 = 𝑅2 = 910 Ω, 𝑅3 = 1 𝑘Ω, and
𝐶1 = 𝐶2 = 47 𝑝𝐹 . Elements highlighted in Fig. 3.33 have following estimated values:
𝑅1′ = 𝑅2′ ≈ 𝑅1 +𝑅𝑝1 ≈ 𝑅2 +𝑅𝑝2 ≈ 1005Ω [193], 𝑅𝑧1 ≈ 860𝑘Ω, 𝐶𝑧1 ≈ 6𝑝𝐹 , and 𝑅𝑧2 ≈
470 𝑘Ω, 𝐶𝑧2 ≈ 14 𝑝𝐹 . We included value of 𝐶𝑧1 and 𝐶𝑧2 to 𝐶1′ ≈ 𝐶1 + 𝐶𝑧1 ≈ 53 𝑝𝐹
and 𝐶2′ ≈ 𝐶2 + 𝐶𝑧2 ≈ 61 𝑝𝐹 . Influence of printed circuit board was not estimated.
Careful routine analysis provides following results in form of more accurate design
equations (oscillation condition and frequency) considering important non-idealities:
𝐴′2 ≥
𝜔0′ ≥
𝑅2′ 𝑅𝑧1 𝑅𝑧2 𝐶1′ (𝑅1′ + 𝑅3 ) + 𝑅1′ 𝑅2′ 𝑅3 (𝑅𝑧1 𝐶1′ + 𝑅𝑧2 𝐶2′ )
,
𝑅1′ 𝑅2′ 𝑅𝑧1 𝑅𝑧2 𝐶1′
⎯
⎸
⎸ 𝐵1 𝐵2 𝑅2 𝑅3 𝑅𝑧1 𝑅𝑧2 𝛼1
⎷
+ [𝑅1′ 𝑅2′ 𝑅𝑧2 (𝐴2 − 1) − 𝑅2′ 𝑅3 (𝑅1′ + 𝑅𝑧2 )]
,
𝑅1′ 𝑅2′ 𝑅3 𝑅𝑧1 𝑅𝑧2 𝐶1′ 𝐶2′
(3.50)
(3.51)
where 𝛼1 represents non-ideal voltage gain (transfer) of voltage buffer (in frame of
CG-CFDOBA). Expected and measured oscillation frequency achieves value 𝑓0 = 3
MHz for selected parameters (𝑅1 = 𝑅2 = 910 Ω, 𝑅3 = 1 𝑘Ω, 𝐶1 = 𝐶2 = 47 𝑝𝐹 ), and
𝐵1 = 𝐵2 = 𝐵1,2 = 1.1 (𝑉𝑆𝐸𝑇 _𝐵1 = 𝑉𝑆𝐸𝑇 _𝐵2 = 𝑉𝑓 0_𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 1.15𝑉 )). Paper [193] explains relation between current gain 𝐵 and control DC voltage (𝐵 ≈ 𝑉𝑆𝐸𝑇 , exactly
valid for 𝑉𝑆𝐸𝑇 < 2𝑉 ). Circuit in Fig. 3.31, resp. Fig. 3.32 requires amplitude
gain control circuit (AGC). We used one of more suitable solutions, which is shown
in Fig. 3.36. Classical low-cost and low-frequency operational amplifiers and diode
doubler are sufficient for these purposes. Resistor 𝑅𝑓 sets slope of input-output
characteristic of AGC circuit (integrator), which ensures smaller or more extensive
reacts on amplitude changes (𝑅𝑓 achieves values from ∞ to hundreds of 𝑘Ω). Because
62
A
1
p
w-
R
B.Ip
Ip
z
1
Cz
CG-BCVA
z
AGC INP
CO control
VDD RP
Vb = Vz
b
z
VSS
VSET_B2 VSET_A2
100 kΩ
2
w
OUT3
b
OUT2
p CG-BCVA
z
R3
R1'
R1
220 Ω 100 kΩ
C1
1 mF
Rf
R3
R2
Cf
R5
1 uF
1 kΩ
2
100 kΩ
R
Z2
Cz2
R4
TL072
1/2
1 kΩ
2x BAT42
C2
TL072
2/2
AGC OUT
Fig. 3.36: Amplitude-automatic gain control circuit for wideband amplitude stabilization.
VCA810 requires negative and decreasing DC control voltage for increasing output
signal level, a voltage inverter is necessary. Outputs of the multiphase oscillator can
be available as input of the AGC circuit (except 𝑂𝑈 𝑇3 ) and output of the AGC is
connected to 𝑉𝑆𝐸𝑇 _𝐴2 . Laboratory measurements of circuit in Fig. 3.31 carried out
following results. We used RIGOL DS1204B oscilloscope and HP4395A network vector/spectrum analyzer (50Ω matching of oscillator’s outputs) for experimental tests.
Fig. 3.37: Measured frequency spectrum of 𝑉𝑂𝑈 𝑇 1 .
63
Fig. 3.38: Measured frequency spectrum of 𝑉𝑂𝑈 𝑇 2 .
Transient responses at all available outputs are depicted in Fig. 3.34. Detailed measurement for quadrature signals across working capacitors (buffered of course) are in
Fig. 3.35 for the highest measured 𝑓0 = 8 𝑀 𝐻𝑧 (𝐵1,2 = 2.9; 𝑉𝑓0 _𝑐𝑜𝑛𝑡𝑟𝑜𝑙 = 3.17 𝑉 ).
Related frequency spectrums are shown in Fig. 3.37, resp. Fig. 3.38. Fig. 3.39 shows
the dependence of 𝑓0 on 𝐵1,2 (𝐵1,2 was adjusted between 0.1 - 2.9). Ideal trace was
10
f0
[MHz]
1
measured
ideal
expected
0
0
1
B 1,2 [-]
Fig. 3.39: Dependence of 𝑓0 on adjustable current gains 𝐵1,2 .
64
10
V OUT1,2 [Vp-p]
0,5
0,4
VOUT1
0,3
0,2
VOUT2
0,1
0
0
1
2
3
4
5
6
7
8
9
f 0 [MHz]
10
Fig. 3.40: Additional characteristics - output levels (𝑉𝑂𝑈 𝑇 1 , 𝑉𝑂𝑈 𝑇 2 ) versus 𝑓0 .
calculated from eq. (3.47). Ideal range of 𝑓0 adjusting was calculated as 0.337 to
9.776 𝑀 𝐻𝑧. Expected estimation based on more accurate eq. (3.51) provides range
from 0.279 to 8.077 𝑀 𝐻𝑧 and range from 0.250 to 8 𝑀 𝐻𝑧 was gained and verified
by laboratory tests. We also tested stability of output level during the tuning process and total harmonic distortion (THD), see Fig. 3.40, resp. Fig. 3.41. Stability of
5
THD
[%]
4
3
VOUT1
2
VOUT2
1
0
0
1
2
3
4
5
6
7
8
Fig. 3.41: Additional characteristics - THD versus 𝑓0 .
65
9
f 0 [MHz]
10
output level during the tuning process changed slightly and output voltage of both
observed outputs was close to 200 𝑚𝑉𝑃 −𝑃 (Fig. 3.40). Measured THD reaches values
lower than 0.5% for 𝑓0 above 2 MHz for both observed output responses (Fig. 3.41).
3.4.3
Quasi–Linear Systems vs. Chaotic Systems
Basic analog building blocks for continuous–time signal processing such as oscillators, filters and amplifiers are initially designed using ideal active elements, i.e.
without considering intrinsic parasitic or non–ideal properties. However these properties can seriously influence global behavior of these electronic systems. Several
facts should be taken into account.
First are typical values of accumulation elements that are, in fact, include error
terms into describing differential equations. Typical value of parasitic capacitor is
tens 𝑝𝐹 and parasitic inductor is tens 𝑛𝐻. Thus unwanted dynamical effects became
significant in the case of high–frequency applications where parasitic inertia elements
became value–comparable to working ones (above 10 𝑀 𝐻𝑧). Serious problems can
be caused by fast dynamical motions and short transients; this situation corresponds
to a right–hand–side of first–order differential equations multiplied by big number.
Parasitic accumulation element should be placed in such a way that it creates bound
between two differential equations reducing degrees of freedom. Second phenomenon
is filtering effects of used active devices. In the case of chaotic oscillator design
roll–off frequencies should be as high as possible. However if regular function of
oscillator, filter or amplifier is required these filtering effects can prevent transitions
to chaotic working regime. Last effect which needs to be considered for electronic
circuit analysis is non–linear
Considering the possibility of increased circuit order and assuming the existence
of transfer nonlinearities naturally quasi–linear block can eventually turn into chaotic
system. If so than harmonic output signals can change into chaotic waveforms with
several typical properties: few harmonics with great phase noise in time domain and
broad–band noise–like frequency spectrum.
66
3.5
Summary
In this chapter, we have proposed several types of electronically adjustable oscillator. Several active elements with adjustable properties (current and voltage gain)
were discussed in this thesis. First of them is very simple electronically adjustable
oscillator employing only two active devices (CCII–) and in the extreme only two
passive elements (capacitors). It allows electronic tuning of the oscillation frequency
and condition of oscillation by DC driving voltage. It was practically tested from
320 𝑘𝐻𝑧 to 1.75 𝑀 𝐻𝑧. Under certain conditions (limited range), the harmonic distortion can be achieved below 1% and the separation of the higher harmonics more
then 50 𝑑𝐵 [221].
Other types are three modified oscillator conceptions that are quite simple, directly electronically adjustable, providing independent control of oscillation condition and frequency in 3R-2C oscillator. The most important contributions of presented solutions are direct electronic and also independent control of CO and 𝑓0 , suitable AGC circuit implementation, buffered low–impedance outputs, and of course,
grounded capacitors [222].
Last type is new oscillator suitable for quadrature and multiphase signal generation. Active element, which was defined quite recently i.e. controlled gain-current
follower differential output buffered amplifier (CG-CFDOBA) [15, 16], and newly
introduced element so–called controlled gain–buffered current and voltage amplifier
(CG-BCVA) were used for purposes of oscillator synthesis. Main highlighted benefits can be found in electronic linear control of oscillation frequency (tested from
0.25 𝑀 𝐻𝑧 to 8 𝑀 𝐻𝑧) and electronic control of oscillation condition. The output levels were almost constant during the tuning process and reached about 200 𝑚𝑉𝑃 −𝑃 .
THD below 0.5% in range above 2 𝑀 𝐻𝑧 was achieved [224].
Operation of the proposed oscillators were verified through simulations and
measurements of the real circuits. Also important parasitic effects in this circuits were discussed in detail. The oscillator was analyzed symbolically, tested by
computer simulations and by laboratory experiments. All types of electronically adjustable oscillator presented in this chapter were described, discussed and published
in[221, 222, 224].
67
4
MODELING OF THE REAL PHYSICAL AND
THE BIOLOGICAL SYSTEMS
4.1
Autonomous Dynamical Systems
Simple system of three autonomous ordinary differential equations (ODEs) with
any nonlinearity can exhibit chaos. When we talk about chaos motion we talk about
a very specific solution of nonlinear dynamical systems which are widely exist in
nature. Therefore, at the present time, research is focused onto relations between
the real physical systems, its mathematical models and circuits realizations. From
this perspective, electronic circuits can be used to modeling and observation of chaos
[159, 162, 171]. The large number of real systems can be described as a system of
the first order differential equations in matrix form of vector field
x ∈ R𝑛 .
ẋ = f(x),
(4.1)
An equilibrium solution of (4.1) is a point x̄ ∈ R𝑛 such that
f(x̄) = 0,
(4.2)
i.e., a solution which does not change in time. Exist a lot of terms which are often substitute for the term “equilibrium solution” as a “fixed point”, “stationary
point”, “rest point”, “singularity”, “critical point” or “steady state.” We will use the
term equilibrium point or fixed point exclusively [179]. The corresponding solution
is 𝜑(x0 ) and is called as a flow. These systems are called autonomous dynamical
systems (ADS) and their phase space representations do not explicitly involve the
independent variable, respectively the vector field f does not explicitly depend on
time 𝑡. It are mathematical models of continuous closed systems without stochastic
processes, evolving input uncertainties over time and at least three degrees of freedom. It all includes the fact that the system is not driven by the external influences
(non-autonomous system). The solution of the ADS is state attractor, the point
motion in the state space. For any dynamic (time changing) system the state atractor is where it will end up eventually. Attractors are semi-group or subsets of the
phase space of a dynamic system. A long time, attractors were thought of as being
simple geometric subsets of the phase space, like points, lines, surfaces, and simple
regions of the three–dimensional space. More complex attractors that cannot be categorized as simple geometric subsets, such as topologically wild sets, were known
of at the time but were thought to be fragile anomalies. Two simple attractors are a
fixed point and the limit cycle. Attractors can take on many other geometric shapes
(phase space subsets). But when these sets (or the motions within them) cannot be
68
easily described as simple combinations (e.g. intersection and union) of fundamental
geometric objects (e.g. lines, surfaces, spheres, toroids, manifolds), then the attractor
is called a strange attractor. The typical example of this attractor is Lorenz attractor. From a qualitative point of view, equilibrium points of the system and their
system stability are very important properties. In the case of deterministic systems
is also crucial non–intersection constraint, which embodies the requirement that a
trajectory in phase space cannot intersect itself [82]. The mathematical foundation
for the non–intersection constraint is a theorem about trajectories of autonomous
systems which states that: “A trajectory which passes through at least one point that
is not a critical point can not cross itself unless it is a closed curve. In this case
the trajectory corresponds to a periodic solution of the system.”[18] The other very
important characteristic of the chaotic system is in extreme sensitivity to the changes of the initial conditions. The behavior is hard to predict in a long time range
[171, 159, 162, 51].It implies that we can not obtain closed–form analytic solution,
so our analysis is restricted to the numerical integration. There is always some uncertainty in the initial state so that any predictions about future behavior are no
longer available.
4.2
Universal Chaotic Oscillator
Neither theoretically nor practically it is not possible to create an electronic circuit
representing all dynamic systems. In our paper we have chosen dynamical systems of
class C [122, 123] because their type of saturation nonlinear global feedback function
is easily electronically realizable. Main contribution is in circuitry implementation
of a fully analog chaotic oscillator with new available active elements, MO-OTA.
The advantage is immediately evident. The smaller number of active elements is in
the whole circuit if compared with implementation using standard voltage–feedback
operatinal amplifier.
4.2.1
Mathematical Model
Consider a general autonomous dynamic system which can be written in following
matrix form:
(︁
)︁
ẋ = Ax + b · ℎ w𝑇 x ,
(4.3)
where
A ∈ R3𝑥3 ,
b ∈ R3 ,
69
w ∈ R3 ,
(4.4)
and ℎ() is a scalar odd-symmetric piecewise linear (PWL) function corresponding
with Fig. 4.1. In this case the scalar saturation nonlinear function
)︁
1 (︁ 𝑇
|w x + 1| − |w𝑇 x − 1| ,
(4.5)
2
separates the state space by two parallel boundary planes into the three affine regions
(︁
)︁
ℎ w𝑇 x =
𝑥˙ = A0 𝑥, D0 region,
(4.6)
𝑥˙ = A1 𝑥 ± b, D±1 regions,
(4.7)
A0 = A1 + bw𝑇 .
(4.8)
where
Therefore, the same corresponding eigenvalues of the characteristic polynomial
describe dynamical motion in both outer segments as well as the geometry of the
vector field. From the previous equations we can conclude that the vector field is
symmetrical with respect to the origin [59]. Practically experiments proved that
a function (PWL) can be smooth. Therefore, practical realization is considerably
simplified, for example with using diodes etc. The PWL approximation is much
more suitable because it leads to the linear section of the state space and allows us
to generate qualitatively equivalent PWL dynamical systems of Class C [74], [124].
We can design the third–order model with Jordan’s state matrix including complex decomposed second–order sub–matrix. However, we need know results of the
second–order model similarity transformation to higher–order model [122]. Assume
that one pair of the eigenvalues is complex conjugate and one eigenvalue is real. This
definition applies for both outer respectively inner regions of the elementary PWL
function (4.5) i.e.
𝑣1,2 = 𝑣 ′ ± 𝑗𝑣 ′′ , 𝑣3 : real; 𝜇1,2 = 𝜇′ ± 𝑗𝜇′′ , 𝜇3 : real.
Fig. 4.1: PWL function.
70
(4.9)
Subsequently the state matrix and the vectors in (4.3) we rewrite in the following
forms
⎛
⎞
⎛
⎞
𝑎11 𝑎12 𝑎13
𝑏1
(︁
)︁
(︁
)︁
⎜
⎟
⎜
⎟
𝑇
𝑇
⎟
⎜
⎟
ẋ = Ax + b · ℎ w x = ⎜
⎝ 𝑎21 𝑎22 𝑎23 ⎠ · x + ⎝ 𝑏2 ⎠ · ℎ w x ,
𝑎31 𝑎32 𝑎33
𝑏3
w 𝑇 x = 𝑤 1 · 𝑥1 + 𝑤 2 · 𝑥 2 + 𝑤 3 · 𝑥3 ,
(4.10)
(4.11)
where 𝑎𝑖𝑗 , 𝑏𝑖 a 𝑤𝑖 parameters are independent of each other.
⎡
⎤
⎣
⎦
𝑣 ′ −𝑣 ′′ −𝜇′ + 𝑣 ′ ⎥
⎢
⎢
(𝜇′ −𝑣 ′ )2 ⎥
⎥,
A = ⎢ 𝑣 ′′ 𝑣 ′
𝑣 ′′ −𝜇′′ 𝐾
⎡
0
𝜇′ − 𝑣 ′
0
⎤
⎡
⎢ (𝜇′ −𝑣′ )2 ⎥
⎥,w
𝑣 ′′ −𝜇′′ 𝐾 ⎦
b=⎢
⎣
𝑣3
𝜇3 − 𝑣3
1
(4.12)
⎤
⎢ 𝑣′′ −𝜇′′ 𝐾 ⎥
⎥,
⎦
𝜇′ −𝑣 ′
=⎢
⎣
(4.13)
1
and the state matrix related with the inner region has the Jordan’s matrix form
⎡
⎢
⎢
⎣
A0 = ⎢
𝜇′
−𝜇′′ 𝐾
𝜇′′ 𝐾 −1
𝜇′
′′
′′ 𝐾
𝜇3 − 𝑣3 (𝜇3 − 𝑣3 ) 𝑣 𝜇−𝜇
′ −𝑣 ′
0
0
𝜇3
⎤
⎥
⎥
⎥.
⎦
(4.14)
The optimization coeficient K of similarity transformation we can express as the real
root of the quadratic equation
𝐾 2 − 2𝐾(𝑀 + 1) + 1 = 0,
⇓
𝐾1,2 = 1 + 𝑀 ±
√︁
(4.15)
𝑀 (𝑀 + 2),
where the parameter M is described in the following form
𝑀=
(𝜇′ − 𝑣 ′ )2 + (𝜇′′ − 𝑣 ′′ )2
> 0, (𝜇′′ , 𝑣 ′′ ̸= 0).
2𝜇′′ 𝑣 ′′
(4.16)
This system model have a very low eigenvalue sensitivity in both the outer and
inner regions of the PWL feedback function [74]. Using a simple transformation of
state variables we can describe behavior of the dynamic system of class C in the
four configurations.
CDCD - dynamic system contain a complex decomposed second-order submatrix,
𝑒11 = 𝑣 ′′ , 𝑒12 = −𝑢′ , 𝑒13 = −𝑣 ′ , 𝑒21 = −𝑣 ′′ ,
′ −𝑣 ′ )2
𝑒22 = −𝑣 ′ , 𝑒23 = − 𝑣(𝜇′′ −𝜇
′′ 𝐾 , 𝑒31 = 𝑣3
𝑣 ′′ −𝜇′′ 𝐾
𝑒32 = −𝑢3 , 𝑒 = 𝜇′ −𝑣′ ,
71
(4.17)
ECEC - dynamic system contain elementary canonically decomposed second-order
submatrix,
𝑒11 = 1, 𝑒12 = −2𝑢′ , 𝑒13 = −2𝑣 ′ ,
(4.18)
𝑒21 = −𝑣 ′ 2 − 𝑣 ′′ 2 , 𝑒22 = 0,
(𝜇′ −𝑣 ′ )2
𝑒23 = − 𝑣′′ −𝜇′′ 𝐾 , 𝑒31 = 𝑣3 , 𝑒32 = −𝑢3 , 𝑒 = 0.,
Last two configurations are combination of two previous.
ECCD
𝑒11 = 1, 𝑒12 = −𝑢′ , 𝑒13 = −2𝑣 ′ ,
𝑒21 = −𝑣 ′ 2 − 𝑣 ′′ 2 , 𝑒22 = 0,
′ −𝑣 ′ )2
𝑒23 = − 𝑣(𝜇′′ −𝜇
′′ 𝐾 , 𝑒31 = 𝑣3 , 𝑒32 = −𝑢3 ,
′′
′′ 𝐾
𝑒 = 𝑣 𝜇−𝜇
′ −𝑣 ′ .
(4.19)
CDEC
𝑒11 = 𝑘𝑣 ′′ , 𝑒12 = −2𝑢′ , 𝑒13 = −𝑣 ′ ,
𝑒21 = −𝐾 −1 𝑣 ′′ , 𝑒22 = −𝑣 ′ ,
′ −𝑣 ′ )2
𝑒23 = − 𝑣(𝜇′′ −𝜇
′′ 𝐾 , 𝑒31 = 𝑣3 , 𝑒32 = −𝑢3 ,
′′
′′ 𝐾
𝑒 = 𝑣 𝜇−𝜇
′ −𝑣 ′ .
(4.20)
Finally the complete state equations of the optimized third-order PWL autonomous
system for circuit realization are given as
[︁ (︁
)︁
]︁
[︁
(︁
)︁]︁
1
−𝑅𝐶 𝑑𝑢
= 𝜀11 𝑢2 + 𝜀12 ℎ w𝑇 u − 𝑢3 + 𝜀13 𝑢1 + 𝑢3 − ℎ w𝑇 u
𝑑𝜏
[︁ (︁
)︁
2
−𝑅𝐶 𝑑𝑢
= 𝜀21 𝑢1 + 𝜀22 𝑢2 + 𝜀23 ℎ w𝑇 u − 𝑢3
𝑑𝜏
[︁ (︁
)︁
]︁
(︁
]︁
(4.21)
)︁
3
−𝑅𝐶 𝑑𝑢
= 𝜀31 ℎ w𝑇 u − 𝑢3 + 𝜀23 ℎ w𝑇 u ,
𝑑𝜏
where
⎛
⎞
1
)︁
⎜
⎟ (︁
𝑇
⎜
·
w u=⎝ 𝜀 ⎟
⇒ w𝑇 u = (𝑢1 + 𝜀 · 𝑢2 + 𝑢3 ) .
𝑢
𝑢
𝑢
1
2
3
⎠
1
(4.22)
Each parameters were obtained from numerical calculations of the individual
transmission coefficients:
𝜀11 = −𝑎12 ,
𝜀12 = − (𝑎11 + 𝑏1 ) ,
𝜀21 = −𝑎21 ,
𝜀31 = 𝑎33 ,
𝜀22 = −𝑎22 ,
𝜀13 = −𝑎11 ,
𝜀23 = −𝑏2
𝜀32 = − (𝑎33 + 𝑏3 ) ,
(4.23)
𝜀 = 𝑤2 .
Parameters shown in Tab. 4.1 were obtained from several different sources for
different ADS systems.
72
Fig. 4.2: Numerical analysis of three different systems configurations from Tab. 4.1
- projection X-Y. Initial condition 𝑖𝑐 = [0.05, 0, 0]𝑇 , DS-ECEC (top), CH2 -ECEC
(center), CH3 -ECEC (bottom).
73
Fig. 4.3: Bifurcaion diagrams (left) and Poincaré map (right) of three selected systems configurations from Tab. 4.1, where 𝑒32 is adopted as a bifurcation parameter.
DS–ECEC (top), CH2 –ECEC (center), CH3 –ECEC (bottom).
74
Tab. 4.1: Parameteres of different dynamical systems.
*
e11
DS
1
0,319 -0,061
DS
1
DS
1
DS
e12
e13
e21
e22
e23
e31
e32
e
configuration
1
-0,061
-0,358
-1,29
-0,728
-1,062
CDCD
0,638 -1,122 -1,004
0
0,092
-1,29
-0,728
0
ECEC
0,319 -0,122 -1,004
0
-0,35
-1,29
-0,728
-0,911
ECCD
-0,273
-1,29
-0,728
0,223
0,844 0,638 -0,061 -1,185 -0,061
CH 1
1
-0,299
-0,3
-1
-0,3
-99
-3
-0,202
-1,01.10
CH 1
1
-0,598
-0,6
-1,09
0
-99
-3
-0,202
0
CH 1
0,999 -0,598
-0,3
CDEC
-5
ECEC
-3
-1,001
-0,3
-99,09
-3
-1
-0,29
-6,79
-1,33
-0,3
-0,034
CDCD
0
-6,648
-1,33
-0,3
0
ECEC
-0,045
0,839
-0,409
-0,272
0,216
CDCD
0
0,816
-0,409
-0,272
0
ECEC
-0,034
0,08
-1,04
-1,474
1,042
CDCD
-1,04
-1,474
0
ECEC
CH 2
1
-0,058 -0,29
CH 2
1
-0,115 -0,58 -1,084
CH 3
1
0,136 -0,045
CH 3
1
0,272 -0,091 -1,002
CH 4
1
0,049 -0,034
-1
-1
CH 4
1
0,097 -0,069 -1,001
CH 5
1
-0,024 0,124
CH 5
1
-0,047 0,248 -1,015
CH 7
1
-0,058 -0,29
CH 7
1
-0,116 -0,58 -1,084
-1
-1
-3
-0,202 -3,028.10
CDCD
CDEC
0
-1,195.10
0,124
0,883
0,277
0,45
-0,167
CDCD
0
0,895
0,277
0,45
0
ECEC
-0,29
-6,79
-1,33
-0,44
-0,034
CDCD
0
-6,648
-1,33
-0,44
0
ECEC
*DS … double scroll *CH i … chaotic attractor i
4.2.2
Mathematical Analysis
Embedded Runge-Kutta fourth order method in MathCAD environment was used
for numerical integration of differential equation system. Parameters of numerical
integration are consistent. Time interval 𝑡(0, 500) and step Δ𝑡 = 10−2 . Fig. 4.2 shows
the plane projections associated with a numerical integration of the mathematical
model. Fig. 4.3 (left side) shows bifurcation diagram for three chosen dynamic system configurations, where 𝑒32 is adopted as a bifurcation parameter. Any point in
the parameter set, where the behavior of dynamical system is unstable is called
bifurcation point, and the set of these points is called a bifurcation set. For the
sufficiently high resolution graph it is necessary to use very small parameter step as
well as to numerically integrate the state space trajectory for the time long enough.
Fig. 4.3 (right side) shows the Poincaré maps of three chosen dynamic systems configurations.
75
Fig. 4.4: Example of block for setting system parameters 𝑒𝑥 .
4.2.3
Universal Chaotic Oscillator Circuit Realization
Synthesis of the electronic circuits is the easiest way how to accurately model the
nonlinear dynamical systems. Main contribution of this part is in circuitry implementation of a universal fully analog chaotic oscillator. Circuitry realization is novel in the sense, that this realization using new available active elements (AD844
[191], MAX435 [196]), simplifies whole circuitry solution. Now let’s focus attention right on the circuitry implementation based on the equation (4.21). Integrator
synthesis was used [60, 112] and the schematic in Fig. 4.5 shows oscillator with
three integrators, one summing amplifier, one PWL function and works in voltage
mode. An operational amplifiers TL084, monolithic operational amplifiers and wideband transconductance amplifier MAX435 were used for circuitry implementation
of mathematical model. The PWL function forms a connection of dual-diode limiters with operational amplifiers TL084. Values of used passive elements were chosen
𝐶1 = 𝐶2 = 𝐶3 = 100 𝑛𝐹, 𝑅1 − 𝑅24 = 1 𝑘Ω, 𝑅25 = 2.7 𝑘Ω, 𝑅26 and 𝑅27 =
10𝑘Ω, 𝑅28 and 𝑅29 = 140 𝑘Ω.
Block in Fig. 4.4 represents the dynamic system parameter 𝑒𝑥 and can be considered as a bifurcation parameter. Circuit is powered by symmetrical ±5 𝑉 and
±15 𝑉 voltage sources. There were used identical values of passive elements from
E24 product line for simulation purposes and also for experimental measurements.
State variables represented output voltage of integrators and therefore are easily measurable. The parasitic properties of the active components are not critical because
we adjusted time constant (RC) in the low–frequency band.
The circuitry implementation functionality was first successfully tested in PSpice
simulator. Fig. 4.6 to Fig. 4.15 shows simulated plane projections associated with a
designed. Correct function of the dynamical system was also verified experimentally.
Plane projections of the selected signals were measured by means of HP 54603B
oscilloscope. Fig. 4.16 to Fig. 4.25 shows photo of plane projection. Fig. 4.26 shows
experimental results in time domain and power spectrum. These measured results are
in a very good accordance with theoretical expectations, i.e. numerical integration of
the given mathematical model. During experimental measurement we have verified
that the time constant can not be much lower than 𝜏 = 10 𝜇𝑠.
76
R1
R2
R3
e
R4
R17
e13
gm
gm
R5
x
c
R18
gm
R6
R7
D1
C1
D2
Vcc Vee
R25
R19
R27
R26
R28
e12
e11
gm
R29
PWL
R20
e22
gm
R10
R12
R11
R8
R13
R14
y
R15
c
R9
R21
e21
gm
R16
C2
R22
e23
gm
R23
e31
gm
z
c
C3
R24
e32
gm
Fig. 4.5: Universal chaotic oscillator schematic.
77
Fig. 4.6: Plane projections, the first row of the Tab. 4.1.
Fig. 4.7: Plane projections, the second row of the Tab. 4.1.
Fig. 4.8: Plane projections, the third row of the Tab. 4.1.
78
Fig. 4.9: Plane projections, the fourth row of the Tab. 4.1.
Fig. 4.10: Plane projections, the fifth row of the Tab. 4.1.
Fig. 4.11: Plane projections, the eight row of the Tab. 4.1.
79
Fig. 4.12: Plane projections, the ninth row of the Tab. 4.1.
Fig. 4.13: Plane projections, the tenth row of the Tab. 4.1.
Fig. 4.14: Plane projections, the thirteen row of the Tab. 4.1.
80
Fig. 4.15: Plane projections, the sixteenth row of the Tab. 4.1.
Fig. 4.16: Experimental results, the first row of the Tab. 4.1. Horizontal axis 2𝑉 /𝑑𝑖𝑣,
vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣 (right).
Fig. 4.17: Experimental results, the second row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣
(right).
81
Fig. 4.18: Experimental results, the third row of the Tab. 4.1. Horizontal axis 2𝑉 /𝑑𝑖𝑣,
vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣 (right).
Fig. 4.19: Experimental results, the fourth row of the table Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
Fig. 4.20: Experimental results, the fifth row of the Tab. 4.1. Horizontal axis 2𝑉 /𝑑𝑖𝑣,
vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣 (right).
82
Fig. 4.21: Experimental results, the eighth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
Fig. 4.22: Experimental results, the ninth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
Fig. 4.23: Experimental results, the twelfth row of the Tab. 4.1.Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
83
Fig. 4.24: Experimental results, the thirteenth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
Fig. 4.25: Experimental results, the sixteenth row of the Tab. 4.1. Horizontal axis
2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
Fig. 4.26: Experimental results in time domain and power spectrum (Agilent Infiniium). Horizontal axis 5 𝑚𝑠𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis
5 𝑚𝑠/𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right).
84
4.3
Inertia Neuron Model
Neural models are used in computational neuroscience and in pattern recognition. In
both cases, the highly parallel nature of the neural system contrasts with the sequential nature of computer systems, resulting in slow and complex simulation software.
More direct hardware implementation holds out the promise of faster emulation,
because it is inherently faster than software and the operation is much more parallel. In fact, direct hardware implementation of neural models has a relatively long
history [146].
Many mathematical models of neuron exist nowadays. One of the first used for
mathematical describing of the neuron behavior was Hodkin–Huxley model. This
model explains the ionic mechanisms underlying the initiation and propagation of
action potentials in the squid giant axon. The simplified version of the Hodgkin–
Huxley is a FitzHugh–Nagumo (FHN) model. FHN model is describing in a detailed
manner activation and deactivation dynamics of a spiking neuron. The other neuron
model conception building upon the FitzHugh–Nagumo model is from J. L. Hindmarsh and R. M. Rose. They proposed a Hindmarsh–Rose (HR) model of neuronal
activity. HR model is described by three coupled first order differential equations.
This extra mathematical complexity allows great variety of dynamic behaviors for
the membrane potential, described by the 𝑥 variable of the model, which include
chaotic dynamics. This makes the Hindmarsh–Rose neuron model very useful, because being still simple, allows a good qualitative description of the many different
patterns of the action potential observed in experiments [187], [17].
4.3.1
FitzHugh–Nagumo Model
One of the simplest models used for mathematical describing of an excitable system
prototype (e.g., a neuron) is FitzHugh–Nagumo model. Fitz Hugh and Nagumo
described regenerative self–excitation by a nonlinear positive–feedback membrane
voltage and recovery by a linear negative–feedback gate voltage. Mathematical model
has the following form
𝑥˙ = 𝑥 − 𝑥3 − 𝑦 + 𝐼𝑒𝑥𝑡
(4.24)
,
𝑦˙ = (𝑥−𝑎−𝑏𝑦)
𝜏
where we have again a membrane voltage 𝑥(𝑡), input current 𝐼𝑒𝑥𝑡 with a slower
general gate voltage 𝑦(𝑡) and experimentally–determined parameters 𝑎 = −0.7, 𝑏 =
0.8, 𝜏 = 1/0.08 [63]. If the external stimulus 𝐼𝑒𝑥𝑡 exceeds a certain threshold value,
the system will exhibit a characteristic excursion in phase space, before the variables
𝑥(𝑡) and 𝑦(𝑡) relax back to their rest values. This behaviour is typical for spike
85
generations (short elevation of membrane voltage) in a neuron after stimulation by
an external input current [187].
4.3.2
Hindmarsh–Rose Model
The neuronal activity of Hindmarsh–Rose (HR) model is study the spiking–bursting
behavior of the membrane potential. Observation is focused to experiments with a
single neuron. The relevant variable is the membrane potential 𝑥(𝑡). Other variables
are 𝑦(𝑡) and 𝑧(𝑡), which include the transport of ions across the membrane through
the ion channels. Variable 𝑦(𝑡) is called spiking and is describing transport of sodium
(Na+ ) and potassium (K+ ) ions through fast ion channels. Variable 𝑧(𝑡) is called
bursting and its function is in transport of other ions (Cl− , Ca+ , . . . ) through slow
channels [50]. Hindmarsh–Rose model is determinated by a system of three nonlinear
ordinary differential equations with dynamical variables 𝑥(𝑡), 𝑦(𝑡), and 𝑧(𝑡). ODEs
have the following form
𝑥˙ = 𝑦 + 𝜑 (𝑥) − 𝑧 + 𝐼
𝑦˙ = 𝜓 (𝑥) − 𝑦
(4.25)
𝑧˙ = 𝜇 (𝑏 (𝑥 − 𝑥0 ) − 𝑧) ,
where
𝜑 (𝑥) = 𝑎𝑥2 − 𝑥3
𝜓 (𝑥) = 1 − 𝐷𝑥2 .
(4.26)
As can be seen from equation (4.25,4.26), system has six parameters: 𝑎, 𝑏, 𝐷, 𝜇, 𝑥0
a 𝐼. The importance of individual parameters are as follows:
∙ 𝐼 . . . represent the membrane input current for biological neurons.
∙ 𝑎, 𝑏 . . . controls switching between bursting and spiking behaviors and allows
to control the spiking frequency.
∙ 𝜇 . . . is rate of change of the slow variable 𝑧. For spiking behavior, 𝜇 allows
controls the spiking frequency. For bursting behavior the number of spikes per
burst is influenced by 𝜇.
∙ 𝐷 . . . governs adaptation. A unitary value of d determines spiking behavior without accommodation and sub threshold adaptation. Whereas, around 𝐷 = 4
give strong accommodation and sub–threshold overshoot, or even oscillations.
∙ 𝑥0 . . . sets the initial conditions of the system [50].
The practical experiments show that it is very common to fix some of them and
let the other to be control parameters. Parameter 𝐼 is the most common parameter
used for controlling of HR model function and is simulated the current that enters
the neuron. Other control parameters used in HR model have the following functions:
86
parameters 𝑎 and 𝑏 simulate the fast ion channels and the parameter 𝑟 simulate the
slow ion channels. Typical values of fixed parameters are: 𝑎 = 3, 𝑏 = 5, 𝐷 = 4,
𝑥0 = −8/5. The parameter 𝜇 is something of the order of 10−3 , and range of 𝐼 is
between −10 and 10.
4.3.3
Circuitry Realization of the Inertia Neuron
Novel circuit implementation is based on integrator synthesis and the mathematical model of the system. Circuitry realization given in Fig. 4.27 consists of three
inverting integrators and amplifiers with TL084 [198] and four analog multipliers
AD633 [188]. [60, 120, 50, 163, 225, 226]. Operational amplifiers TL084 [198] are
used for realizations of inverting integrator and one operational amplifier for realizations summing amplifier. State variables are represented by the output voltage
of integrators and therefore are easily measurable. Parasitic properties of the active
components are not critical because the time constant circuit is selected in the audio
band. The nonlinear two–port circuit is formed by a connection of two four–quadrant
R9
R11
R10
R8
R1
R2
TL084
x
C1
TL084
A D633
X1
A D633
X1
W
X2
Y1
R3
W
X2
Y1
Z
Y2
Y2
Z
TL084
R12
V2
A D633
X1
W
X2
Y1
Y2
R4
C2
y
C3
z
R5
A D633
X1
TL084
R7
R13
W
TL084
X2
V1
Z
Y1
V4
Y2
Z
V3
R14
R6
TL084
Fig. 4.27: Schematicm of the fully analog representation of single inertia neuron.
87
analog multipliers AD633 with transfer function:
𝑈𝑊 = 𝐾 (𝑈𝑋1 − 𝑈𝑋2 ) · (𝑈𝑌 1 − 𝑈𝑌 2 ) + 𝑈𝑍 ,
(4.27)
where constant 𝐾 = 0, 1 is given by the internal structure of multiplier [188]. In the
given schematic voltage 𝑉1 = 1 𝑉 represents constant term 1 in (4.26), voltage 𝑉2
corresponds to parameter 𝐼 divided by 100, voltage 𝑉3 and 𝑉4 defines parameter 𝑏 and
𝑥0 respectively. Other system parameters are defined by gains, namely parameter
a by resistor 𝑅1 0 and parameter 𝑑 by resistor 𝑅1 4. Time constant of circuit is
determined by the capacitors 𝐶1 = 𝐶2 = 𝐶3 = 100 𝑛𝐹 as well as the associated
resistors 𝑅1 = 𝑅2 = 𝑅3 = 𝑅4 = 𝑅5 = 1 𝑘Ω, 𝑅7 = 100 𝑘Ω𝑎𝑛𝑑𝑅8 = 10 Ω. In practice
the DC sources are replaced by voltage dividers realized by the potentiometers.
Fig. 4.28: Simulated results of the inertia neuron obtained from PSpice - Monge
plane projection.
88
Drawback of the proposed circuit is in the necessity of many integrated circuits.
Fig. 4.29: Simulated results of the qualitatively different behavior of the HR model.
𝑎 = 2, 6; 𝑏 = 4; 𝑑 = 5; 𝜇 = 0, 01; 𝐼 = 2, 99; (𝑎) 𝑥0 = −0, 6; (𝑏) 𝑥0 = −1, 6;
(𝑐) 𝑥0 = −2, 0; (𝑑) 𝑥0 = −2, 4.
4.3.4
Simulation and Measurement Results
The functionality of the inertia neuron circuit implementation was first successfully
tested by PSpice simulation environment. Fig. 4.28 shows plane projections associated with simulation of the inertia neuron. Correct function of the dynamical system
was verified also experimentally. Plane projections and frequency spectrum of the selected signals measured by means of Agilent Infinium digital oscilloscope are shown
in Fig. 4.30. The simulated results (Fig. 4.29) and measured (Fig. 4.31) of the qualitatively different behavior of HR model in time domain are demonstrated. It can
be see for 𝑥0 = −0.6 system exhibits spiking behavior. If we change this bifurcation
parameter to 𝑥0 = −1.6 the system begins to exhibit chaotic behavior (chaotic dynamics is obtained for a small range around value 𝑥0 = −1.6). With other change
of 𝑥0 is system exhibits bursting dynamics. It is evident that all the main dynamics
of a neuron (spiking, bursting and chaos) can be obtained with the proposed circuit
by properly setting the control parameters. It eventually turns out that this system
is not as sensitive as expected.
89
Fig. 4.30: Measured results of the inertia neuron – plane projection and frequency
spectrum (Agilent Infiniium). Horizontal axis 2 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣.
90
Fig. 4.31: Measured results of the qualitatively different behavior of the HR model(Agilent Infiniium). 𝑎 = 2, 6; 𝑏 = 4; 𝑑 = 5; 𝜇 = 0, 01; 𝐼 = 2, 99; (𝑎) 𝑥0 = −0, 6;
(𝑏) 𝑥0 = −1, 6; (𝑐) 𝑥0 = −2, 0; (𝑑) 𝑥0 = −2, 4. Horizontal axis 50 𝑚𝑠/𝑑𝑖𝑣, vertical
axis 2 𝑉 /𝑑𝑖𝑣.
91
4.4
Nóse–Hoover Thermostat Dynamic System
The aim of this section is in the new circuit implementation of the Nóse–Hoover
thermostat dynamic system
𝑥˙ = 𝑦,
(4.28)
𝑦˙ = −𝑥 − 𝑦𝑧,
2
𝑧˙ = 𝛼 (𝑦 − 1) ,
where the dot denotes differentiation with respect to time t.
Julien C. Sprott [162] first time mention about chaotic solutions of the NóseHoover equation discribing thermostat system. An unique property of this system
is that it is conservative equilibrium–less system whereas all the other chaotic ADS
(a)
(d)
x
y
z
(b)
x
z
2
y
(e)
6
y
x 4
-4
x 2
-2
y
-2
(c)
-6
2
y
(f)
z 1
-1
6
y
z 6
-6
-2
-6
Fig. 4.32: Numerical simulation of the Nóse-Hoover thermostat system – periodic
(left side), chaotic (right side).
92
Fig. 4.33: Map curve of the sensitivity to change of initial conditions for the smooth
Nóse-Hoover ADDS in the time domain.
are dissipative having single or more fixed points. Hoover [52] pointed out that the
conservative system (4.28) found by Sprott is a special case of the Nóse-Hoover
thermostat dynamic system which one had been earlier shown [121] to exhibit time
reversible Hamiltonian chaos. Note that this case in general needs an adjustable
parameter, but it turns out that chaos occurs for all coefficients equal to unity, and
so it is especially simple in that sense. None of the systems found by Sprott with
a single quadratic nonlinearity share that property, although there are two other
chaotic cases with all unity coefficients and two quadratic nonlinearities with strange
attractors [162]. This system is also special in that chaos is observed for only a small
range of initial conditions. For example, one possibility is (𝑥, 𝑦, 𝑧) = (0, 5, 0).
For sufficiently large 𝛼 the regions of phase space in which regular orbits are
possible are surrounded by regions in which the oscillator generates chaotic trajectories. Fig. 4.32 shown perspective state trajectories of the Nóse–Hoover ther-
93
(a)
4
z
(d)
-10
y 10
10
z
-6
y 6
-4
(b)
-10
6
z
(e)
y 6
-6
20
z
y 6
-6
-20
-6
(c)
6
z
(f)
y 6
-6
40
z
y 6
-6
-6
-40
Fig. 4.34: Poincare map of sections 𝑦 vs. 𝑧 at plane 𝑥 = 0 of the Nóse-Hoover
thermostat system.
mostat system with a smooth vector field obtained by numerical simulation. The
complexity of this structure changes is increased with changes 𝛼. During studies of
this system were observed typical types of attractors, a limit cycle (𝑎 − 𝑐), quasi
periodic orbit and chaos (𝑑 − 𝑒), but generally for different values of the initial
condition(𝐼𝐶1 = (0 5 0)𝑇 ; 𝐼𝐶2 = (0 1.55 0)𝑇 ). Fig. 4.33 illustrates sensitivity of the
system to changes of initial conditions. Difference between the reference trajectory
and pertubation trajectory is for the 𝐼𝐶 = (0 5 + 0.1 0)𝑇 . We can see that two
close solutions diverge from each other and we can again expected general validity
of sensitivity to changes of initial conditions. Here, as in other case, iteration step
was Δ𝑡 = 0.01.
Behavior of the Nóse–Hoover thermostat system is also possible observed by
Poincare maps. In such map, regular trajectories produce either a finite string of
94
Fig. 4.35: Bifurcation diagram of the Nóse-Hoover thermostat system, where bifurcation parameter is sensitivity to change of initial conditions.
dots along the surface of a KAM (Kolmogorov-Arnold-Moser) torus [19], if a winding
ratio is a rational number, or a closed loop for irrational winding ratios. Chaotic
trajectories generate instead a filled or at least fractal region with dimensionality
greater than two and dimensionality greater than one in the Poincare map. Fig. 4.34
shows series of such Poincare map for sections 𝑦 vs. 𝑧 at plane 𝑥 = 0 and increasing
𝛼. It also allows us qualitative analysis of the whole state space reduce to the study of
W
X1
X2
Y1
Y2
Z
W
X1
X2
Y1
Y2
Z
CCII+
o X
R4
1V
Z
Y
R5
CCII+
Y o
X
R1
CCII+
Y o
Z
Z
X
C1
R2
CCII+
Y o
Y
X
Z
C2
R3
X
Z
C3
Fig. 4.36: Circuit realization of the Nóse-Hoover thermostat system with AD844 as
a non–inverting integrator.
95
two–dimensional space. It should be stressed that these maps are independent of the
value of the Hamiltonian and, consequently, of the initial conditions as long as the
latter are in the big stochastic domain of the phase space. In principle, the Poincare
sections of Fig. 4.34 cover an infinite range rather than finite range of the y–z plane.
The bifurcation diagrams for the Nóse–Hoover thermostat (Fig. 4.35) shows rich
dynamics composed of chaotic region, chaos-order transitions and periodic orbits. It
would be interesting to study the field dependence of the attractor in more detail,
e.g., according to which scenario does the transitions from order to chaos occur, is the
dynamics nonergodic for certain parameters as it has been found for the Gaussian
thermostated Lorentz gas [86] and where are the chaotic and the integrable regions.
4.4.1
Circuitry Implementation of the Nóse–Hoover System
Circuitry implementation of the Nóse–Hoover thermostated system is based on the
ordinary differential equations (4.25) and realized as integrator synthesis. State variables are represented by the output voltage of integrators and therefore are easily
measurable.Fig. 4.36 shows schematic of the Nóse–Hoover thermostat system oscillator with three integrators, two multipliers and works in voltage mode. For circuitry implementation of mathematical model are used four operational amplifiers
AD844 [191] which are realized as non–inverting integrators and inverter. The in5. 0V
12V
8V
2. 5V
4V
0V
0V
- 4V
- 2. 5V
- 8V
- 5. 0V
- 2. 0V
V( y)
5. 0V
- 1. 0V
0V
V( x )
1. 0V
2. 0V
- 12V
- 8. 0V - 6. 0V
V( y)
12V
- 4. 0V
- 2. 0V
0V
V( x )
2. 0V
4. 0V
- 8V
- 4V
0V
V( z )
4V
8V
6. 0V 8. 0V
8V
2. 5V
4V
0V
0V
- 4V
- 2. 5V
- 8V
- 5. 0V
- 6. 0V
- 4. 0V
V( y )
- 2. 0V
0V
V( z)
2. 0V
4. 0V
6. 0V
- 12V
- 16V
- 12V
V( y)
12V
16V
Fig. 4.37: Simulation results of the Nóse-Hoover oscillator – periodic (left
side),chaotic (right side).
96
tegrated circuit AD844 provides an extra node which acts as the output voltage
follower. These buffered outputs allow us to observe other combinations of state
variables without affecting the proper function of the oscillator. The quadratic nonlinear two–port circuit is formed by connection of the two four–quadrant analog
multipliers AD633 [188]. Values of used passive elements were chosen 𝐶1 = 𝐶2 =
𝐶3 = 100 𝑛𝐹, 𝑅1 = 𝑅2 = 1 𝑘Ω, 𝑅3 = 𝑅4 = 𝑅5 = 10 𝑘Ω and the oscillator is
powered by the symmetrical ±15 𝑉 voltage source.
4.4.2
Simulation and Measurement Results
The Nóse–Hoover oscillator circuitry implementation functionality was tested by
PSpice simulation environment. Fig. 4.37 shows simulated plane projections associated with a designed of Nóse–Hoover oscillator. Correct function of the dynamical
system was verified also experimentally. Fig. 4.38 shows plane projections of the
selected signals which were measured by means of Agilent Infinium digital oscilloscope. In both case (simulation and measurement) we can see development in the
motion from periodic cycle to strange attractor. The agreement between simulation
and measurement is very good.
Fig. 4.38: Measurements results of the Nóse-Hoover oscillator – periodic (left side),
chaotic (right side). Horizontal axis 500 𝑚𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣(top left), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 5 𝑉 /𝑑𝑖𝑣(top right), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical
axis 2𝑉 /𝑑𝑖𝑣(bottom left), horizontal axis 5𝑉 /𝑑𝑖𝑣, vertical axis 5𝑉 /𝑑𝑖𝑣(bottom right)
97
4.5
Algebraically Simple Three–Dimensional ODE’s
In this section, we used one of the systems, which published J. C. Sprott [160] as
an example of chaotic system. Equations (4.29) have been choosen on the base of
simple non–linearity.
𝑥˙ = 𝑎𝑥 + 𝑧,
(4.29)
𝑦˙ = 𝑥𝑧 − 𝑦,
𝑧˙ = −𝑥 + 𝑦.
4.5.1
Mathematical Analysis
In the most publications [51, 159] the authors start with the mathematical model
analysis together with the numerical solution of the system parameters. Assume
the class of third–order autonomous deterministic dynamical system with single
equilibria located at the origin. An example of such system is (4.29), where 𝑎 is
the real parameter. Fig. 4.39 shows convergence plot of the 𝐿𝐸𝑚𝑎𝑥 (𝑎 = 0.42) and
numerical values are following
𝐿𝐸𝑚𝑎𝑥1 = 0.151, 𝐿𝐸𝑚𝑎𝑥2 = 0.142, 𝐿𝐸𝑚𝑎𝑥3 = −0.653.
(4.30)
J. Sprott has computed, that for 𝑎 = 0.4, system behave chaotic [160]. How can we
see from bifurcation diagram (Fig. 4.40) there are many real parameters 𝑎 for which
system solution is chaotic. The positions of equilibria (critical) points are independent on the parameter and are located at 𝑓1 = [0, 0, 0]𝑇 and 𝑓2 = [−2.5, −2.5, 1]𝑇 .
Investigation of vinicity around point f1 is given by
𝑑𝑒𝑡(𝜆I − J) = 0
(4.31)
Fig. 4.39: Convergence plot of the largest Lyapunov exponents for 𝑎 = 0.42.
98
Fig. 4.40: Bifurcation diagram of the Sprott system (4.29).
Jacobian matrix of this system is following
⎞
⎛
0.4 0 1
⎟
⎜
⎜
J = ⎝ 𝑧 −1 𝑥 ⎟
⎠,
−1 1 0
(4.32)
and is leading to the characteristic polynomial. For critical point 𝑓1 is following
⎞
⎛
𝜆 − 0.4
0
−1
⎟
⎜
⎜
𝑑𝑒𝑡(𝜆I − J) = ⎝
0
𝜆+1 0 ⎟
⎠=
1
−1
𝜆
(4.33)
= 𝜆3 + 0.6𝜆2 + 0.6𝜆 + 1 = 0,
and for critical point 𝑓2 is following
Fig. 4.41: Numerical simulation of system (4.29) for 𝑎 = 0.37 – limit cycle (left side)
and for 𝑎 = 0.42 – chaos (right side).
99
Fig. 4.42: Sensitivity to initial conditions in the time domain.
⎞
⎛
𝜆 − 0.4
0
−1
⎟
⎜
⎜
𝑑𝑒𝑡(𝜆I − J) = ⎝
1
𝜆 + 1 −2.5 ⎟
⎠=
1
−1
𝜆
(4.34)
= 𝜆3 + 0.6𝜆2 + 3.1𝜆 − 1 = 0.
The set of parameters for critical point 𝑓1 and 𝑓2 leads to the following real and a
Fig. 4.43: Numerical simulation of system (4.29) for 𝑎 = 0.42.
100
R2
R3
R4
R1
C1
X
W
Z
R5
X1
X2
Y1
Y2
R6
C2
R7
C3
R8
Y
Z
Fig. 4.44: Schematic of the Sprott system circuitry realization.
pair of complex conjugated eigenvalues:
𝑓1 : 𝜆1,2 = 0.2 ± 0.98𝑖
𝑓2 : 𝜆4,5 = −0.449 ± 1.779𝑖
𝜆3 = −1,
𝜆6 = 0.297.
(4.35)
(4.36)
In this case system have two real eigenvalues and two complex-conjugate pair (socalled saddle focus).
Embedded Runge-Kutta fourth order method in MathCAD environment is used
for numerical integration of differential equation system. Parameters of numerical
integration are consistent. Time interval 𝑡(0, 500) and step size Δ𝑡 = 10−2 . Sensitivity to initial conditions in the time domain is evident from Fig. 4.42. The plane 2–D
and 3–D projections associated with a numerical integration of the mathematical
model are shown in Fig. 4.41 and Fig. 4.43.
4.5.2
Circuitry Realization
The schematic of the oscillator with three integrators, one summing amplifier, one
multipliers and works in voltage mode is shown in Fig. 4.44. For circuitry implementation of mathematical model are used four operational amplifiers TL084 [198].
101
Fig. 4.45: Numerical simulation of the Sprott system (4.29) for 𝑎 = 0.42 – chaos.
Advantage is that in one package are four amplifiers. The nonlinear two–port circuit
is formed by a connection of two four–quadrant analog multipliers AD633 [188].
Values of used passive elements were chosen 𝐶1 = 𝐶2 = 𝐶3 = 100 𝑛𝐹, 𝑅1 = 𝑅4 =
𝑅6 = 𝑅7 = 𝑅8 = 1 𝑘Ω, 𝑅5 = 100 Ω, 𝑅3 = 400 Ω. Resistor 𝑅2 = 100 Ω represented
value of the parameter 𝑎. Circuit is powered by symmetrical ±15 𝑉 voltage source.
Fig. 4.46: Measured data of realized circuit for 𝑅6 = 400Ω. Horizontal axis 𝑉1
500𝑚𝑉 /𝑑𝑖𝑣, vertical axis 𝑉2 1𝑉 /𝑑𝑖𝑣.
102
4.5.3
Simulation and Measurement Results
The circuitry implementation functionality was first successfully tested by PSpice
simulator. Simulated plane projections associated with a designed are shown in
Fig. 4.45. Correct function of the dynamical system was verified also experimentally.
Plane projections of the selected signals were measured by means of HP 54603B oscilloscope. Plane projection photos are shown in Fig. 4.46. The agreement between
numerical solution, simulation and measurement is very good.
103
4.6
Chaotic Circuits Based on OTA Elements
Lately, several authors [133, 112, 151, 222] have been successfully used the operational transconductance amplifier (OTA) as the main active element in continuous–time
active filters and especially for the nonlinear chaotic systems realizations [103, 104,
2]. In 1989 Sanchez–Sinencio et al. [133] showed that the OTA, as the active element
in basic building blocks, can be also efficiently used for nonlinear continuous–time
function synthesis. OTA has only a single high–impedance node, in contrast to conventional operational amplifiers. This makes the OTA an excellent device candidate
for high–frequency and voltage (or current) programmable analog basic building
blocks [133]. In this section is a simple authentication how to simply realize a real
physical systems electronically by using OTAs elements. During the practical realization of the chaotic oscillator below the new unpublished chaos system with one
quadratic nonlinearity and one PWL function has been discovered.
Consider the same algebraically simple three-dimensional ODEs with six terms
and one nonlinearity [160] as multiple of two state variables as in a previous section
section 4.5 in the general form
𝑥˙ = 𝑎𝑥 + 𝑧
𝑦˙ = 𝑥𝑧 − 𝑦
𝑧˙ = −𝑥 + 𝑦
(4.37)
and a new algebraically simple three-dimensional ODEs with six terms, one quadratic nonlinearity and one PWL function
𝑥˙ = −𝑏𝑥 − 4𝑦
𝑦˙ = 𝑓 (𝑥) + 𝑧 2
𝑧˙ = 1 + 𝑥
(4.38)
where 𝑎 and 𝑏 can be considered as bifurcations parameters [159].
⎧
⎪
⎪
⎨
−23 if 𝑥 < −0.4
𝑓 (𝑥) = ⎪ 59𝑥 if −0.4 ≤ 𝑥 ≤ 0.5
⎪
⎩
32
otherwise
(4.39)
J. Sprott computed and described countless of simple chaotic flows [160]. For such
systems, the positions of equilibria (critical) points are independent on the parameter
Tab. 4.2: Position of critical points according to the system with PWL function.
x < −0.4
(−1, 0.625, 4.769)
(−1, 0.625, −4.769)
−0.4 ≤ x ≤ 0.5
(−1, 0.625, 7.681)
(−1, 0.625, −7.681)
104
x > 0.5
(−1, 0.625, 5.657𝑖)
(−1, 0.625, −5.657𝑖)
Fig. 4.47: Bifurcation diagram of system (4.37), bifurcation parameter is sensitivity
to change of parameter 𝑎.
and are located for first system at (0, 0, 0) and (−2.5, −2.5, 1). In comparison, the
second system has several solutions. All of them are dependent on the PWL function
where the state space is divided into three segments. The positions of the critical
points were computed for the individual segments and are shown in the table (see
Tab. 4.2). A complex solution for 𝑥 > 0.5 means that there is no critical point.
Investigation of vinicity around critical point is given by (4.40).
𝑑𝑒𝑡(𝜆I − J) = 0
(4.40)
Jacobian matrix, characteristic polynomial and eigenvalues of the first system
were computed in previous section 4.5. Values of the eigenvalues are shown in table
(see Tab. 4.3). Therefore, our attention were concentrated on computation of eigenvalues of the second system with PWL function. Jacobian matrix of the first area
Fig. 4.48: Bifurcation diagram of system (4.38), bifurcation parameter is sensitivity
to change of parameter 𝑏.
105
Tab. 4.3: Numerically calculated eigenvalues of both systems.
Critical points
Eigenvalues
1𝑠𝑡 chaotic system
𝜆1,2 = 0.2 ± 0.98𝑖, 𝜆3 = −1
𝜆4,5 = −0.449 ± 1.779𝑖, 𝜆6 = 0.297
2𝑛𝑑 chaotic system
𝜆1,2 = 0.969 ± 2.768𝑖, 𝜆3 = −4.437
𝜆4,5 = −2.606 ± 2.711𝑖, 𝜆6 = 2.713
𝜆7 = −16.78, 𝜆8 = 14.02, 𝜆9 = 0.261
𝜆10 = −16.54, 𝜆11 = 14.30, 𝜆12 = −0.26
(0, 0, 0)
(−2.5, −2.5, 1)
(−1, 0.625, 4.769)
(−1, 0.625, −4.769)
(−1, 0.625, 7.681)
(−1, 0.625, −7.681)
(𝑥 < −0.4) is following
⎛
⎞
−2.5 −4 0
⎜
⎟
J=⎜
0 2𝑧 ⎟
⎝ 0
⎠,
1
0 0
(4.41)
and is substituted to the characteristic polynomial. For critical point (−1, 0.625, 4.769)
is following
⎛
⎞
𝜆 + 2.5 4
0
⎟
⎜
⎟=
𝑑𝑒𝑡(𝜆I − J) = ⎜
0
𝜆
9.538
⎝
⎠
−1
0
𝜆
(4.42)
= 𝜆3 + 2.5𝜆2 + 38.152 = 0.
The local behavior of the system near the origin is uniquely determined by the
gm3
x.z
gm2
gm1
X
C1
Y
C2
Z
G
C3
Fig. 4.49: Circuitry implementation of Eq.(4.37) using OPA860. The capacitors are
470 𝑛𝐹 , the resistor is 1 𝑘Ω and except for the variable resistor (adjustable from 0
to 1 𝑘Ω).
106
eigenvalues, which are shown in table (see Tab. 4.3). Now, let’s focus our attention
on bifurcation analysis. If we consider parameter 𝑎 resp. 𝑏 as bifurcation parameter,
we can compute bifurcation diagram shown in Fig. 4.47 resp. Fig. 4.48. As we can
see, there are many real numbers 𝑎 resp. 𝑏 for which system has chaotic solution
[109]. Bifurcation diagrams were generated by Mathcad.
4.6.1
Circuitry Realization
The circuit design procedure is based on classical circuit synthesis [60, 112]. Parasitic properties of the active components aren’t critical because the time constant circuit is selected in the low band. Operational transconductance amplifiers
OPA860 [197] are used for circuitry implementation of mathematical models. Nonlinearities are formed by connection of four–quadrant analog multipliers AD633
[188] or using transfer characteristics of OPA860 [197] in saturation. The schematics of the oscillators are shown in Fig. 4.49 resp. Fig. 4.50. Values of used
passive elements were chosen 𝐶1 = 𝐶2 = 𝐶3 = 470 𝑛𝐹 , 𝑅 = 1 𝑘 (variable),
𝑔𝑚1 = 1𝑚𝑆, 𝑅𝑆𝐸𝑇 1 = 250Ω, 𝐼𝑆𝐸𝑇 1 = 11.2𝑚𝐴, 𝑔𝑚2 = 1𝑚𝑆, 𝑅𝑆𝐸𝑇 2 = 250Ω, 𝐼𝑆𝐸𝑇 2 =
11.2𝑚𝐴, 𝑔𝑚3 = 1𝑚𝑆, 𝑅𝑆𝐸𝑇 3 = 250Ω, 𝐼𝑆𝐸𝑇 3 = 11.2𝑚𝐴. Circuit is powered by symmetrical voltages ±5 𝑉 (OTA) resp. ±15 𝑉 (AD633). Simulation results in Fig. 4.51
to Fig. 4.58 corresponding with planes 𝑎 to 𝑑 in Fig. 4.47, resp. Fig. 4.48.
gm3
gm2
z2
gm1
X
C1
Z
Y
G
C2
I
C3
Fig. 4.50: Circuitry implementation of Eq.(4.38) using OPA860. The capacitors are
470𝑛𝐹 , DC current source is 1 𝑚𝐴, the resistor is 1 𝑘Ω and except for the variable
resistor (adjustable from 0 to 1 𝑘Ω).
107
5.0V
5.0V
2.5V
2.5V
0V
0V
-2.5V
-2.5V
-5.0V
-6.0V
V(x)
-4.0V
-2.0V
0V
2.0V
-5.0V
-6.0V
V(x)
4.0V
-4.0V
-2.0V
V(z)
Fig. 4.51: Simulation results for the
circuit realized according to the Eq.
4.37 (see Fig. 4.47) - 𝑅 = 950 Ω.
Plane projection X-Z corresponds
with plane 𝑎 in bifurcation diagram
(see Fig. 4.47) - period 2.
5.0V
2.5V
2.5V
0V
0V
-2.5V
-2.5V
-4.0V
-2.0V
2.0V
4.0V
Fig. 4.52: Simulation results for the
circuit realized according to the Eq.
4.37 (see Fig. 4.47) - 𝑅 = 800 Ω.
Plane projection X-Z corresponds
with plane 𝑏 in bifurcation diagram
(see Fig. 4.47) - period 4.
5.0V
-5.0V
-6.0V
V(x)
0V
V(z)
0V
2.0V
-5.0V
-6.0V
V(x)
4.0V
V(z)
-4.0V
-2.0V
0V
2.0V
4.0V
V(z)
Fig. 4.54: Simulation results for the
circuit realized according to the Eq.
4.37 (see Fig. 4.47) - 𝑅 = 735 Ω.
Plane projection X-Z corresponds
with plane 𝑑 in bifurcation diagram
(see Fig. 4.47) - chaos.
Fig. 4.53: Simulation results for the
circuit realized according to the Eq.
4.37 (see Fig. 4.47) - 𝑅 = 785 Ω.
Plane projection X-Z corresponds
with plane 𝑐 in bifurcation diagram
(see Fig. 4.47) - period 8.
108
0.5V
0.5V
0V
0V
-0.5V
-0.5V
-1.0V
-1.0V
-1.5V
-1.5V
-2.0V
-2.0V
-2.5V
4.0V
4.2V
V(x)
4.4V
4.6V
4.8V
5.0V
-2.5V
4.0V
4.2V
V(x)
5.2V
4.4V
Fig. 4.55: Simulation results for the
circuit realized according to the Eq.
4.38 (see Fig. 4.48) - 𝑅 = 245 Ω.
Plane projection X-Z corresponds
with plane 𝑎 in bifurcation diagram
(see Fig. 4.48) - period 2.
0.5V
0V
0V
-0.5V
-0.5V
-1.0V
-1.0V
-1.5V
-1.5V
-2.0V
-2.0V
4.4V
4.6V
4.8V
5.0V
5.2V
Fig. 4.56: Simulation results for the
circuit realized according to the Eq.
4.38 (see Fig. 4.48) - 𝑅 = 260 Ω.
Plane projection X-Z corresponds
with plane 𝑏 in bifurcation diagram
(see Fig. 4.48) - period 4.
0.5V
-2.5V
4.0V
4.2V
V(x)
4.6V
V(z)
V(z)
4.8V
5.0V
-2.5V
4.0V
4.2V
V(x)
5.2V
V(z)
4.4V
4.6V
4.8V
5.0V
5.2V
V(z)
Fig. 4.57: Simulation results for the
circuit realized according to the Eq.
4.38 (see Fig. 4.48) - 𝑅 = 275 Ω.
Plane projection X-Z corresponds
with plane 𝑐 in bifurcation diagram
(see Fig. 4.48) - period 8.
Fig. 4.58: Simulation results for the
circuit realized according to the Eq.
4.38 (see Fig. 4.48) - 𝑅 = 271 Ω.
Plane projection X-Z corresponds
with plane 𝑑 in bifurcation diagram
(see Fig. 4.48) - chaos.
109
4.7
Chaotic Circuit Based on Memristor Properties
This section provides an innovative practical realization of a memristor based chaotic circuit. Forty years ago today, the memristor was postulated as the fourth circuit
element by Leon O. Chua [57, 58]. In a seminal paper [164], which appeared on 1
May 2008 issue of Nature, a team led by R. Stanley Williams from the HewlettPackard Company announced the fabrication of a passive solid–state two–terminal
device called the memristor. It thus took its place along side the rest of the more
familiar circuit elements such as the resistor, capacitor and inductor. The common
thread that binds these four elements together as the four basic elements of circuit
theory is the fact that the characteristics of these elements relate the four variables
in electrical engineering (voltage, current, flux and charge) intimately [100]. The
memristor element, with memristance M, provides a functional relation between
charge and flux, 𝑑𝜙 = 𝑀 𝑑𝑞 [164]. Last five years, the research of circuits containing
memristor is becoming a hot topic in the circuit theory and chaos. Over this period,
chaotic attractor has been observed in many autonomous memristor based chaotic
circuits and many authors papers uses a passive nonlinearity based on memristor
[61, 100, 101, 102, 10, 175, 128, 178, 186, 184]. Chaotic oscillator containing memristor still attracts attention. One of the first memristor based chaotic circuit was
Fig. 4.59: Numerical simulation in MathCAD and Poincare section (blue dots) which
is formed by 𝑥 − 𝑧 plane sliced at 𝑦 = 0 (green surface).
110
Y
2
1
1
0
Z
0
2
1
2
4
1
3
2
1
0
1
2
3
4
3
2
1
0
1
2
X
X
Fig. 4.60: Plot of 𝑥(𝑡) versus 𝑦(𝑡) (left) and 𝑥(𝑡) versus 𝑧(𝑡) (right) plane projection
of the chaotic attractor generated by Eq. (4.43) - numerical solution.
proposed by Itoh and Chua in 2008 [61]. In this case and many others, memristor
represents nonlinear function (e.g., Chua’s diode) and together with other elements
(e.g. resistors, capacitors and inductors) is possible to realize a simple chaotic oscillators [61, 100, 10, 178, 186, 62]. Many others authors also deals with modeling and
realization of memristor [173, 13, 111, 180, 21, 34, 24]. Nevertheless, this part is not
concentrated on memristor elements realization itself. Its nonlinear and dynamical
properties are used for the realization of a simple chaotic system, where the memristor function is integral part of circuit. In this part is presented memristor based
chaotic circuit synthesis based on mathematical model published by Muthuswamy
and Chua [101]. Muthuswamy and Chua used the classical operational amplifier as
the basic building block for circuit synthesis. Compared to them we used an operational transconductance amplifier with a single output (OTA) and multiple output
(MO-OTA). This step led to the simplify the overall circuit structure and we saved
one active element.
4.7.1
Mathematical Analysis
Consider the three–element circuit with the memristor properties [101]. The equations for the memristor based chaotic circuit are described by set of follows an ordinary
differential equations (ODE)
𝑥˙ = 𝑦
𝑦˙ = − 13 𝑥 + 12 𝑦 − 12 𝑧 2 𝑦
𝑧˙ = −𝑦 − 𝛼𝑧 + 𝑧𝑦,
111
(4.43)
Fig. 4.61: Time domain curve of the system system sensitivity to the changes in
initial conditions. Initial conditions: 𝑥0 = 0.1, 𝑦0 = 0, 𝑧0 = 0.1 and 𝛼 = 0.6
(continuous trace), 𝑥𝑛0 = 0.11, 𝑦𝑛0 = 0, 𝑧𝑛0 = 0.11 and 𝛼 = 0.6 (dashed trace).
112
0.8
0.6
0.4
LEmax [−]
0.2
0
−0.2
−0.4
−0.6
−0.8
0
100
200
300
400
500
t [s]
600
700
800
900
1000
Fig. 4.62: Convergence plot of the largest Lyapunov exponents determined by
Eq. (4.43); 𝛼 = 0.6.
where parameter 𝛼 = 0.6 can be considered as a bifurcation parameter. Please note
that our memristor based chaotic circuit is based on a memristive device defined
by Chua and Kang in 1976 [58] and not the ideal memristor defined by Chua in
1971 [57]. System behavior is dependent on the value of many parameters and includes various types of solutions (periodic, quasi–periodic or chaos). Fig. 4.59 shows a
3D plot of the attractor obtained by the numerical simulation of Eq. (4.43) (initial
conditions: 𝑥(0) = 0.1, 𝑦(0) = 0, 𝑧(0) = 0.1) by a program MathCAD. Blue dots
in Fig. (4.59) represents a Poincare section (the intersection of a periodic orbit in
the state space of a continuous dynamical system with a certain lower dimensional subspace transversal to the flow of the system). Embedded Runge–Kutta fourth
order method in a MathCAD environment was used for a numerical integration of
differential equation system. The parameters of the numerical integration are consistent. Time interval was 𝑡(0, 500) and step was Δ𝑡 = 10−2 . The chaotic attractors
projections associated with the numerical integration of the mathematical model are
shown in Fig. 4.60. Fig. 4.61 illustrates system sensitivity to the changes in initial
conditions. Difference between a reference trajectory and a perturbation trajectory
is for 𝐼𝐶1 = (0.1 0 0.1)𝑇 and 𝐼𝐶2 = (0.11 0 0.11)𝑇 . We can see that two close solutions diverge from each other and we can expect general validity of this claim. The
position of equilibria (critical) point is independent on the system parameters and
is located at 𝑓 = [0, 0, 0]𝑇 (black dot in Fig. 4.59). Investigation of vinicity around
point 𝑓 is given by
𝑑𝑒𝑡(𝜆I − J) = 0.
113
(4.44)
Fig. 4.63: Bifurcation diagram generated by Eg. (4.43). The bifurcation parameter
𝛼 is shown on the horizontal axis of the plot.
The Jacobian matrix of this system is
⎞
⎛
0
1
⎜
1 2
1
⎜
J = ⎝ −3 −2𝑧 +
0
𝑧−1
1
2
0
⎟
−𝑦𝑧 ⎟
⎠,
𝑦 − 0.6
(4.45)
and leads to a characteristic polynomial. For critical point 𝑓 is following
⎛
⎞
−1
0
⎜ 1
⎟
⎜
⎟=
𝑑𝑒𝑡(𝜆I − J) = ⎝ 3 𝜆 − 0.5
0
⎠
0
1
𝜆 + 0.6
𝜆
(4.46)
= 𝜆3 + 0.1𝜆2 + 0.033𝜆 + 0.2 = 0.
The local behavior of the system near the origin is uniquely determined by the
eigenvalues
𝜆1,2 = 0.25 ± 0.52𝑖,
𝜆3 = −0.6.
(4.47)
In this case system have one real negative eigenvalue and one complex–conjugate
pair of positive eigenvalues. This type of geometry is called saddle–focus. Fig. 4.62
shows convergence plot of the 𝐿𝐸𝑚𝑎𝑥 (𝛼 = 0.6) and numerical values are following
𝐿𝐸𝑚𝑎𝑥1 = 0.0276, 𝐿𝐸𝑚𝑎𝑥2 = 0.0006, 𝐿𝐸𝑚𝑎𝑥3 = −0.584.
(4.48)
Fig. 4.63 shows bifurcation diagram generated by Eg. (4.43). We choosed the parameter 𝛼 as the bifurcation parameter in the range 0.01 ≤ 𝛼 ≤ 0.6. Bifurcation
diagram shows that there exists many real numbers 𝛼 for which is system solution
chaotic.
114
Memristor
ISET1
ISET3
gm1
gm3
ISET2
gm2
X1
X2
Y1
Y2
Z
W
X1
X2
Y1
Y2
Z
R1
X
C1
R2
W
Y
C2
Z
R3
C3
Fig. 4.64: Circuit realization of the chaotic system with OTA (OPA860), MO-OTA
(MAX435) and analog multiplier (AD633) based on Eq. (4.43). Capacitors are 470nF
and resistors are 𝑅1 = 15 Ω, 𝑅2 = 100 Ω. Resistor 𝑅3 should be adjustable from 0 to
1 𝑘Ω.
4.7.2
Circuitry Realization
The circuit design procedure is based on classical circuit synthesis and the proposed circuit works in hybrid voltage/current mode [60, 112]. An advantage of this
implementation is evident in comparison with older publication [101]: a smaller number of passive and active circuit elements. Operational transconductance amplifier
OPA860 [197] and multiple output transconductance amplifier MAX435 [196] are
used for circuitry implementation of the mathematical model equations (4.43).Nonlinearities are formed by a connection of four–quadrant analog multipliers AD633
[188]. High (10 MΩ) input resistances make signal source loading negligible. Therefore, we can straight connect input 𝑌2 of the first multiplier to the output 𝑊
of the second multiplier. We used this components for practical verification of a
function, especially MAX435. We can use two OPA860 as replacement of MAX435
115
and up to date alternative. The schematic of the chaotic oscillator is shown in
Fig. 4.64. Values of used passive elements were choosen 𝐶1 = 𝐶2 = 𝐶3 = 470 𝑛𝐹 ,
𝑅1 = 15 Ω, 𝑅2 = 100 Ω and 𝑅3 = 600 Ω (variable). We used the following simplifications: 𝑔𝑚1 = 31 𝑚𝑆, 𝑅𝑆𝐸𝑇 1 = 250 Ω, 𝐼𝑆𝐸𝑇 1 = 11.2 𝑚𝐴, 𝑔𝑚2 = 12 𝑚𝑆, 𝑅𝑆𝐸𝑇 2 =
250 Ω, 𝐼𝑆𝐸𝑇 2 = 11.2 𝑚𝐴, 𝑔𝑚3 = 1 𝑚𝑆, 𝑅𝑆𝐸𝑇 3 = ∞, 𝐼𝑆𝐸𝑇 3 = 450 𝜇𝐴. Circuit is
powered by symmetrical voltages ±5 𝑉 (OTA and MO-OTA) resp. ±15 𝑉 (AD633).
4.7.3
Simulation and Measurement Results
The circuitry implementation functionality was first successfully tested in PSpice simulator. Fig. 4.65 resp. Fig. 4.66 show simulation results. Figure 4.65 was obtained
by data export from the PSpice to the MathCAD environment and was processed to
the 3D plot. Correct function of the dynamical system was also verified experimentally on the breadboard. Plane projections of the selected signals were measured by
means of an oscilloscope HB 54603B. Fig. 4.67 shows a photo of the measurement
results – projection of chaotic attractor onto 𝑥 − 𝑦 plane. Comparison of results
proved a rather good agreement between numerical simulation, PSpice simulation
and measurement.
Fig. 4.65: Simulation in PSpice with indication of the 𝑥 − 𝑧 plane sliced at 𝑦 = 0
(green surface)
116
Fig. 4.66: Plot of 𝑣𝑥 (𝑡) versus 𝑣𝑦 (𝑡) (left) and 𝑣𝑥 (𝑡) versus 𝑣𝑦 (𝑡) (right) plane projection of the chaotic attractor – PSpice simulation.
Fig. 4.67: Measured data of realized circuit (Fig. 4.64). Horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣,
vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal axis 500𝑚𝑉 /𝑑𝑖𝑣, vertical axis 1 𝑉 /𝑑𝑖𝑣
(right).
117
4.8
Nonautonomous Dynamical Systems
As mentioned in the previous section, an autonomous dynamical systems are systems whose phase space representations do not explicitly involve the independent
variable (time 𝑡) and have at least three degrees of freedom. But there also exist
mathematical models of dynamical systems with two degree of freedom and one independent variable. Those systems are called a nonautonomous dynamical systems
(NDS). [159] For a nonautonomous system is specific, that the current time 𝑡 and
time of the initialization 𝑡0 are important rather than just their difference. The very
simple generalization of a semi—group formalism to nonautonomous dynamical systems is the two parameter semi–group or process formalism of a nonautonomous
dynamical system, where both 𝑡 and 𝑡0 are the parameters. The other formalism
includes an nautonomous dynamical systems as a driving mechanism which is responsible for, e.g., the temporal change of the vector field of a nonautonomous
dynamical system [72]. If we consider an initial value for a nonautonomous ordinary
differential equation in R𝑛 we can use following mathematical formalism:
ẋ = 𝑓 (𝑡, 𝑥) ,
𝑥 (𝑡0 ) = 𝑥0 .
(4.49)
In comparison with an autonomous dynamical systems, the solutions now depend
separately on the actual time 𝑡 and the initialization time 𝑡0 rather than only on
the elapsed time 𝑡 − 𝑡0 since initialization [72]. In the following section are described
some mathematical models of nonautonomous dynamical systems with a sinusoidally
varying driving force [159, 171].
4.8.1
Van der Pol Oscillator (a)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
=𝑦
= −𝑥 + 𝑏 (1 − 𝑥2 ) 𝑦 + 𝐴 sin 𝜔𝑡,
(4.50)
where 𝑏 = 3, 𝐴 = 5, 𝜔 = 1, 788 are typical values of the parameters and initial
conditions are 𝑥0 = −1, 9, 𝑦0 = 0, 𝑡0 = 0.
4.8.2
Shaw–Van der Pol Oscillator (b)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
= 𝑦 + 𝐴 sin 𝜔𝑡
= −𝑥 + 𝑏 (1 − 𝑥2 ) 𝑦,
(4.51)
where 𝑏 = 1, 𝐴 = 1, 𝜔 = 2 are typical values of the parameters and initial conditions
are 𝑥0 = 1, 3, 𝑦0 = 0, 𝑡0 = 0.
118
4.8.3
Duffing–Van der Pol Oscillator (c)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
=𝑦
= 𝜇 (1 − 𝛾𝑥2 ) 𝑦 − 𝑥3 + 𝐴 sin 𝜔𝑡,
(4.52)
where 𝜇 = 0, 2, 𝛾 = 8, 𝐴 = 0, 35, 𝜔 = 1, 02 are typical values of the parameters
and initial conditions are 𝑥0 = 0, 2, 𝑦0 = −0, 2, 𝑡0 = 0.
4.8.4
Two–well Duffing Oscillator (d)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
=𝑦
= −𝑥3 + 𝑥 − 𝑏𝑦 + 𝐴 sin 𝜔𝑡,
(4.53)
where 𝑏 = 0, 25, 𝐴 = 0, 4, 𝜔 = 1 are typical values of the parameters and initial
conditions are 𝑥0 = 0, 2, 𝑦0 = 0, 𝑡0 = 0.
4.8.5
Rayleygh–Duffing Oscillator (e)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
=𝑦
= 𝜇 (1 − 𝛾𝑦 2 ) 𝑦 − 𝑥3 + 𝐴 sin 𝜔𝑡,
(4.54)
where 𝜇 = 0, 2, 𝛾 = 4, 𝐴 = 0, 3, 𝜔 = 1, 1 are typical values of the parameters and
initial conditions are 𝑥0 = 0, 3, 𝑦0 = 0, 𝑡0 = 0.
4.8.6
Ueda Oscillator (f)
𝑑𝑥
𝑑𝑡
𝑑𝑦
𝑑𝑡
=𝑦
= −𝑥3 − 𝑏𝑦 + 𝐴 sin 𝜔𝑡,
(4.55)
where 𝑏 = 0, 05, 𝐴 = 7, 5, 𝜔 = 1 are typical values of the parameters and initial
conditions are 𝑥0 = 2, 5, 𝑦0 = 0, 𝑡0 = 0 are initial conditions.
4.8.7
Ueda Oscillator Methematical Anlysis
In the next section 4.8.8 are presented two equivalent circuits realization of the
sinusoidally driven chaotic oscillators which are based on the state model equations
description. For example, in the engineering we can found these equations in the
description of the large elastic structure deformation. Another example of chaotic
systems in engineering are driven pendulums. Ueda’s oscillator is one example of such
system and can be assumed as a biologically and physically important dynamical
model exhibiting chaotic motion. System have two degrees of freedom and chaotic
119
Fig. 4.68: Numerical simulations of the nonautonomous dynamical systems with a
sinusoidally varying driving force.
attractor in some parameter domains. The system described by a nonlinear second
order differential equation can be also describe in a following matrix form:
⎛
⎞
⎛
⎞ ⎛
⎞
⎛
⎞
⎛
⎞
0
𝑥˙ ⎠ ⎝ 0 1 ⎠ ⎝ 𝑥1 ⎠ ⎝ 0 ⎠ ⎝
⎠,
⎝
+
+
=
·
𝑥¨
𝐴 sin (𝜔𝑡)
−𝑥3
0 −𝑏
𝑥2
(4.56)
where 𝐴, 𝑏 and 𝜔 real numbers and can be consider as the natural bifurcation parameters. Nonlinear properties of dynamical system are represented by a nonlinear
cubic vector field
⎛
⎞
0 ⎠
f (x) = ⎝
.
−𝑥3
(4.57)
An example of time series solution 𝑥 respectively 𝑦 versus 𝑡 obtained by numerical
integration of (4.56) is presented in Fig. 4.69. How we can see this time projection
has a ragged appearance, which persists for as long as time integrations are carried
out. Maybe someone can argue that certain patterns in the waveform repeat themselves at irregular intervals, but there is never exact repetition, and the motion is
truly non–periodic. At first, we focus on numerical integration (4.56) in the time
120
Fig. 4.69: Divergence of nearby trajectories caused by small changes in initial conditions in time domain.
domain and the divergence of state variables for different initial conditions. The
reason for this is that, when two identical systems are started in nearly identical
initial conditions, the two motions diverge from each other at an exponential rate.
Of course, if we will consider the same initial conditions, then the equation guarantees that the motions are identical for all time. But since some uncertainty in
the initial condition is inevitable with real physical systems, the divergence of nominally identical motions cannot be avoided in the chaotic regime. This is illustrated in
Fig. 4.69. Two numerical integrations starts at the same time but with a very small
differences in initial conditions - black (continuous trace) versus red (dashed trace).
The two adjacent trajectories are close to each, but after the short time rapidly
become uncorrelated. On the average, their separation increases by a fixed multiple
for any given interval of elapsed time. Because of the exponential divergence it is
impossible to impose long–term correlation of the two motions by reducing the initial perturbation, since each order of magnitude improvement in initial agreement is
eradicated in a fixed increment of time [171]. Embedded Runge-Kutta fourth order
method in MathCAD environment is used for numerical integration of differential
121
Fig. 4.70: Poincare maps of Ueda Attractor.
equation system. Parameters of numerical integration are consistent and following:
time interval 𝑡 ∈ (0, 200)), step Δ𝑡 = 10−2 and the initial conditions 𝑥0 = (0, 10)𝑇 .
The plane projections associated with a numerical integration of the mathematical
model Ueda’s oscillator are shown in Fig. 4.72 . In this figure are shown plane projections for stable parameters 𝑏 = 0, 05, 𝐴 = 7, 5 and changing parameter 𝜔 over
the range 1 < 𝜔 < 2, 5. The last trajectory projected onto the XY plane is a strange
attractor called the Ueda attractor. Further we can see development in the motion
from periodic cycle to strange attractor (Ueda attractor). Fig. 4.70 shows Poincare
maps of Ueda Attractor and Fig. 4.71 shows bifurcation diagrams of Ueda Attractor.
Fig. 4.71: Bifurcation diagrams – dependence on the angular velocity of the driven
signal (left side) and dependence on the amplitude of the driven signal (right side).
122
Fig. 4.72: The Ueda oscillator plane projection dependent on the change of the driven
frequency - numerical integration.
123
4.8.8
Circuitry Realization
Two systems based on the ordinary differential equations of the Ueda oscillator (4.56)
are presented. Integrator synthesis [60] is again used for circuitry implementation
of the Ueda oscillator. State variables are represented by the output voltage of
integrators. Parasitic properties of the active components are not critical because
the time constant circuit is selected in the audio band.
4.8.9
Simulation and Measurement Results – Voltage Mode
The schematic of the first solution Ueda oscillator with two integrators, two multipliers and works in voltage mode is shown in Fig. 4.73. For circuitry implementation of mathematical model are used two operational amplifiers TL084 [198] which
are realized inverting voltage integrators. The cubic nonlinear two–port circuit is
formed by a connection of two four–quadrant analog multipliers AD633 [188]. Values of used passive elements were chosen 𝐶1 = 𝐶2 = 15𝑛𝐹 , 𝑅1 = 𝑅3 = 10𝑘Ω,
𝑅2 = 200𝑘Ω, 𝑅4 = 100Ω and the oscillator is powered by the symmetrical ±15𝑉
voltage source. The frequency of driven sinusoidal signal was changing over the range
1, 5𝑘𝐻𝑧 < 𝑓 < 4𝑘𝐻𝑧 and amplitude was 7.5𝑉 . The same values of the used passive
elements were for simulation and practical measurement.
The functionality of circuitry implementation of Ueda oscillator was first successfully tested in PSpice simulator. Simulated plane projections associated with
X1
X2
Y1
Y2
Z
W
W
X1
X2
Y1
Y2
Z
R4
R2
R1
C1
Y
C2
X
R3
u1(t)
Fig. 4.73: Circuitry implementation of the mathematical model in voltage mode.
124
a designed of Ueda oscillator are shown in Fig. 4.74. Correct function of the dynamical system was verified also experimentally. Plane projections and frequency
spectrum of the selected signals were measured by means of Agilent Infinium digital oscilloscope and are shown in Fig. 4.75. The simulated results (Fig. 4.74) and
measured (Fig. 4.75) of the qualitatively different behavior of the Ueda oscillator in
time domain are demonstrated. We can see development in the motion from periodic cycle to strange attractor for the changing parameter 𝑓 . The agreement between
simulation and measurement is very good.
Fig. 4.74: The plane projections of the chaos oscillator obtained from PSpice simulation – voltage mode.
125
Fig. 4.75: Measured results of the chaos oscillator in voltage mode – plane projections
and frequency spectrum (Agilent Infiniium). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis
1 𝑉 /𝑑𝑖𝑣
126
4.8.10
Simulation and Measurement Results – Hybrid Mode
The schematic of the second solution Ueda oscillator also with two integrators, two
multipliers however works in hybrid mode is shown in Fig. 4.76. In this case are used
two operational amplifiers AD844 [191] works as a current integrator. The cubic nonlinear two–port circuit is also formed by a connection
of two four–quadrant
analog
X1
X1
X2
X2
multipliers AD633. Values of used passive elements were chosen 𝐶1 = 𝐶2 = 15 𝑛𝐹 ,
W
W
Y1
Y1
Y2 also powered
𝑅1 = 𝑅5 = 1 𝑀 Ω, 𝑅2 = 20 𝑘Ω, 𝑅3 = 𝑅4 = Y2
1 𝑘Ω and the oscillator was
Z
Z
by the symmetrical ±15𝑉 V voltage source. The frequency of driven sinusoidal sigR4
nal was changed over the same range (1, 5𝑘𝐻𝑧 < 𝑓 < 4𝑘𝐻𝑧) and amplitude was
R2 elements were for simulation and practi750𝑚𝑉 . The same values of the used passive
cal measurement. The functionality of the second circuitry implementation of Ueda
C1
R1
oscillator was again successfully
tested in PSpice
Ysimulator (Fig. 4.77) and measured
C2
X again
by means of Agilent Infinium digital oscilloscope (Fig. 4.78). We can conclude
that the agreement between simulation and measurement is very good. By utilizing
R3
the hybrid mode or current
mode integrated circuits allows
an engineer to create an
u1(t)
oscillator ready for the higher frequency applications as is demanded in these days.
Y
C
X
C
R1
R3
C1
X1
X2
Y1
Y2
Z
R2
C2
R4
X1
X2
Y1
Y2
Z
W
R5
W
u1(t)
Fig. 4.76: Circuitry implementation of the mathematical model in hybrid mode.
127
Fig. 4.77: The plane projections of the chaos oscillator obtained from PSpice simulation – hybrid mode.
128
Fig. 4.78: Measured results of the chaos oscillator in hybrid mode – plane projections
and frequency spectrum (Agilent Infiniium). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis
2 𝑉 /𝑑𝑖𝑣
129
4.9
Summary
In this chapter, circuitry implementations of autonomous and nonautonomous chaotic systems have been presented, analysed and published:
∙ novel circuitry implementation of the universal and fully analog chaotic oscillator works in hybrid mode based on the optimized dynamical system of
class C with piecewise–linear (PWL) feedback [209],
∙ novel fully analog circuitry implementation of he inertia neuron model [200],
∙ novel circuitry implementation of the Nóse–Hoover thermostated dynamic system [218],
∙ algebraically simple three–dimensional ODE’s chaotic oscillator based on OTA
elements [211],
∙ modified algebraically simple three–dimensional ODE’s with one quadratic
nonlinearity and one PWL function chaotic circuit based on OTA elements
[211],
∙ novel chaotic circuit based on memristor properties and OTA elements [213],
∙ novel voltage mode and hybrid mode circuitry implementation of nonautonomous dynamical system [207].
Many simulations and laboratory experiments proved a good agreement between
numerical integration, practical simulation and measurement. These qualitative observations were supported with computer simulations and practical experiments.
The exponential divergence of trajectories that underlies chaotic behavior, and the
resulting sensitivity to initial conditions, lead to long–term unpredictability which
manifests itself as deterministic randomness in the time domain.
130
5
ANALOG–DIGITAL SYNTHESIS OF THE
NONLINEAR DYNAMICAL SYSTEMS
In this section we would like to study third order nonlinear system, where such
behavior is very rare [28]. We are presenting a generalized method for generating 2D
𝑚 𝑥 𝑛 grid scroll, where a special case of solution is set of 1D grid scrolls [158, 172].
The chosen 2D 𝑚 𝑥 𝑛 scroll attractor can be in fact considered as particular case of
Chua’s attractor [143]. Of course similar approach can be utilized for 3D grid scrolls
by adding another nonlinear functional block. Our solution involves only analog to
digital converters (AD) and digital to analog converters (DA) for implementation of
the nonlinear function. It comes to this, that there is no need for any microcontroller.
5.0.1
Mathematical Analysis
The model describing chaotic 2D 𝑚 𝑥 𝑛 scroll generation is described by three
first–order differential equations.
ẋ = A x + B 𝜙(C x).
(5.1)
Matrix A and B are represented as
⎛
⎞
⎛
⎞
0
1
0
0 −1 0
⎜
⎟
⎜
⎟
⎜
⎟
⎜
A=⎝ 0
0
1 ⎠ , B = ⎝ 0 0 −1 ⎟
⎠,
−𝑎 −𝑏 −𝑐
𝑎 𝑏
𝑐
(5.2)
matrix C is an identity matrix and function 𝜙(.)
⎛
⎞
⎛
⎞
1 0 0
𝑓 (𝑥)
⎜
⎟
⎜
⎟
⎜
⎟
⎜
C = ⎝ 0 1 0 ⎠ , 𝜙 = ⎝ 𝑓 (𝑦) ⎟
⎠,
0 0 1
0
(5.3)
For numerical integration the embedded Runge-Kutta fourth order method in MathCAD
environment with variable step is used. Where 𝑥˙ represents first order derivatives.
Function 𝑓 (.) denotes a nonlinear step function. Parameters 𝑎, 𝑏 and 𝑐 are constants.
For synthesis of the nonlinear step function, connecting the ADC directly with the
DAC generate step transfer function. Defining step
Δ=
𝐷𝑦𝑛𝑎𝑚𝑖𝑐𝑎𝑙 𝑟𝑎𝑛𝑔𝑒[𝑉 ]
𝑁 𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑏𝑖𝑡𝑠[−]
Then output value with steps is defined as
131
(5.4)
Fig. 5.1: The model of step function 𝑓 (𝑥) for 2𝑏 (black) and for 5𝑏 (gray).
𝑜𝑢𝑡(𝑥) =
⎧
⎪
⎨ł
Δ+
Δ
2
if 𝑥 > 0
⎪
⎩𝑙
Δ−
Δ
2
if 𝑥 < 0,
(5.5)
where
𝑥
∧ 𝑙 ∈ N.
(5.6)
Δ
Where N stands for set of natural numbers. Then model representing ADC connected
directly to DAC, the step function with saturation can be written as
𝑙=
𝑓 (𝑥) =
⎧
⎪
⎪
𝑜𝑢𝑡(𝑥)
⎪
⎪
⎨
if |𝑥| < Ψ
Δ
−Ψ + 2
⎪
⎪
⎪
⎪
⎩Ψ − Δ
2
where Ψ can be expressed as Ψ =
if 𝑥 ≤ −Ψ
(5.7)
if 𝑥 ≥ Ψ,
𝐷𝑦𝑛𝑎𝑚𝑖𝑐𝑎𝑙 𝑟𝑎𝑛𝑔𝑒[𝑉 ]
.
2
Such system (5.1) with function (5.7) and with constants set to 𝑎 = 𝑏 = 𝑐 = 0.8
can be seen in Fig. 5.2 and Fig. 5.3. Where the both functions (5.7) consists of 4
levels. That is equal to utilizing 2 bit AD/DA converters.
5.0.2
Circuitry Realization
To synthesize circuit from differential equations system (5.1), integrator synthesis
was chosen. After thinking about how to reduce the complexity of the nonlinear
network a very simple circuitry has been revealed. Only few basic building blocks
are necessary: inverting integrators, summing amplifier, AD and DA converters and
voltage sources. Electronic circuit system consists of three integrator circuits (using
132
Fig. 5.2: Numerical simulation of system (5.1), the Monge’s projections 𝑉 (𝑥) vs.
𝑉 (𝑦).
Fig. 5.3: Numerical simulation of system (5.1), the Monge’s projections 𝑉 (𝑦) vs.
𝑉 (𝑧).
133
R1
R2
f(x)
R3
R4
R5
C1
C2
R6
C3
R7
R8
R9
R10
R11
R12
R13
f(y)
R14
Fig. 5.4: The block schematics of realization of equations (5.1).
operational amplifier AD713 [189]), which integrate the equations (5.1). Values of
passive parts are estimated directly from the equations. The circuitry realization
is in Fig. 5.4. In order to ensure Nyquist–Shannon sampling criterion for the converters, frequency renormalization is an easy and straightforward process covering
identical change of all integration constants simultaneously. To create step transfer
functions 𝑓 (𝑥) and 𝑓 (𝑦), the data converters are used. The schematics in Fig. 5.5
shows the data converters connected directly to produce step transfer function. In
order to process positive and negative voltages, the circuit is divided in the two
S YNC
S YNC
A/D
D/A
ROUT
INP UT
OUTP UT
S YNC
S YNC
A/D
D/A
ROUT
Fig. 5.5: The block schematics of realization of function 𝑓 (𝑥) using data converters.
134
2.0V
1.0V
0V
-1.0V
-2.0V
-2.0V
-1.5V
-1.0V
-0.5V
0.0V
0.5V
1.0V
1.5V
2.0V
Fig. 5.6: The simulations from PSpice program, V(x)versus V(y) projections.
branches. Voltage sources are used as references for the converters. The circuitry
realization was evaluated using PSpice. The overall simulation time is set to 100 𝑚𝑠.
The simulated output of Monge’s projections is in the Fig. 5.6 to Fig. 5.8. The values
of passive resistors are 𝑅1 = 𝑅13 = 118 𝑘Ω, 𝑅2 = 𝑅5 = 𝑅9 = 𝑅11 = 𝑅12 = 100 𝑘Ω,
𝑅3 = 𝑅4 = 𝑅10 = 125 𝑘Ω, 𝑅6 = 𝑅7 = 𝑅8 = 𝑅14 = 1 𝑘Ω, 𝑅𝑂𝑢𝑡 = 1 Ω and values of
the capacitors are 𝐶1 = 𝐶2 = 𝐶3 = 100 𝑛𝐹 .
5.0.3
Simulation and Measurement Results
It should be pointed out that hardware implementation of 2D 𝑚 𝑥 𝑛 scroll chaotic
attractors is very difficult technically [88] and in [89], despite there is no theoretical
limitation in the mathematical model for generating the large numbers of the multidimensional scrolls. The above circuit design method provides a theoretical principle
for hardware implementation of such chaotic attractors with multidirectional orientations and a satisfactory number of scrolls. The measurements presented in Fig. 5.9
to Fig. 5.14 were done using HP 54645D oscilloscope.
135
2.0V
1.0V
0V
-1.0V
-2.0V
-4.0V
-3.0V
-2.0V
-1.0V
0.0V
1.0V
2.0V
3.0V
4.0V
Fig. 5.7: The simulations from PSpice program, V(x)versus V(y) projections.
(A) simulace.dat (active)
4.0V
2.0V
0V
-2.0V
-4.0V
-8.0V
-6.0V
-4.0V
-2.0V
0V
2.0V
4.0V
6.0V
8.0V
Fig. 5.8: The simulations from PSpice program, V(x)versus V(y) projections.
136
Fig. 5.9: 1–D 4 scroll. Projections V(x) vs V(-y) (left), V(-y) vs V(z) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical
axis 2 𝑉 /𝑑𝑖𝑣 (right).
Fig. 5.10: 1–D 16 scroll. Projections V(x) vs V(-y) (left), V(-y) vs V(z) (right).
Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (left), horizontal axis 1 𝑉 /𝑑𝑖𝑣,
vertical axis 500 𝑚𝑉 /𝑑𝑖𝑣 (right).
Fig. 5.11: Measured system, 2x2 scroll. Projections V(x) vs V(-y) (left), V(-y) vs
V(z) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis
1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right).
137
Fig. 5.12: Measured system, 4x4 scroll. Projections V(x) vs V(-y) (left), V(-y) vs
V(z) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis
1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right).
Fig. 5.13: Measured system - perturbation of parrameters, 6x4 scroll (left) and 4x2
scroll (right). Projections 𝑉 (𝑥) vs. 𝑉 (−𝑦). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis
2 𝑉 /𝑑𝑖𝑣 (left), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right).
Fig. 5.14: Measured system, 6x6 scroll. Projections 𝑉 (𝑥) vs. 𝑉 (−𝑦) (left), 8x8 scroll,
projections 𝑉 (𝑥) vs. 𝑉 (−𝑦) (right). Horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣
(left), horizontal axis 1 𝑉 /𝑑𝑖𝑣, vertical axis 2 𝑉 /𝑑𝑖𝑣 (right).
138
Fig. 5.15: Numerically simulated 3D (10,10,10) grid scolls.
5.0.4
3D Grid Scrolls
By simple modification of the matrix B and the matrix function 𝜙(.) as follows
⎛
⎞
⎛
⎞
0 −1 0
𝑓 (𝑥)
⎜
⎟
⎜
⎟
⎜
⎟
⎜
B = ⎝ 0 0 −1 ⎠ , 𝜙 = ⎝ 𝑓 (𝑦) ⎟
⎠,
𝑑 𝑏
𝑐
𝑓 (𝑧)
(5.8)
one can obtain by setting constant 𝑎 = 𝑏 = 𝑐 = 0.8 and 𝑑 = 0.77 3D (𝑘, 𝑙, 𝑚) grid
scolls. Where the constant 𝑘, 𝑙, 𝑚 stands for the number of levels of the nonlinearity
(5.7).
139
5.1
Summary
In this chapter, the well known 2D 𝑚 𝑥 𝑛 scroll system was chosen and was realized
utilizing novel approach using the data converters as non-linear functions. With the
growing order of the system, the presence of chaotic behavior is more probable. First
the models were derived to simulate the data converters connected directly (ADCDAC). Than the connection was reduced to produce less scrolls. Other crux is in the
verify chaotic behavior of proposed conception. The circuit simulator PSpice was
used for theoretical verify and then the circuit prototype was build and measured.
The simulation results and measurements prove a good final agreement between
theory and practice and were published in[219].
140
6
ON THE POSSIBILITY OF CHAOS DESTRUCTION VIA PARASITIC PROPERTIES OF
THE USED ACTIVE DEVICES
Anyhow theoretically such analysis can solve problems if desired chaotic pattern is
structurally stable and have potential for the practical applications. If such stability
can not be satisfied to some degree the desired chaotic attractor is not experimentally
observable.
Common worst-case analysis is probably not a correct approach to determine
structural stability of the state space attractors in the case of the nonlinear vector
field since largest LE is not a monotonic function of the parasitic elements. In other
words crucial perturbation of the flow can not necessarily appear for the border
values of the combined parasitic properties. It seems that largest LE should be provided in a hyper–dimensional tabularized fashion. It is evident that it is impossible
to consider the parasitic properties of the individual active devices separately; both
from the viewpoint of confusing visualization and enormous time demands required
for calculation. Thus to quantify the influence of the non–ideal properties of the
active devices on the desired strange attractors a term generalized parasitic can be
introduced. It means that parasitic effects which have the same nature are applied
on the mathematical model of chaotic oscillator together. The simplest such generalized parasitic effects are additional dissipation, parameters uncertainty and loss
integration. Positive largest LE indicates a system solution which is sensitive to the
changes of the initial conditions while zero value denotes a limit cycle (no matter
how complex it looks like).
Parasitic properties of the active devices have accumulating tendencies; it means
that one basic error term is not generally compensated by the other. In OTA based
realizations parasitic capacitor which belongs to the input impedance is connected in
parallel with working one and enlarges time constant. Input resistance is responsible
for increased dissipation of dynamical flow; if this property crosses critical value a desired strange attractor collapse into the simpler geometrical structure, i.e. limit cycle
or, if dissipation is extremely strong, a fixed point. In CCII based oscillators input
resistance of X-terminal is connected in series with working resistor causing again
a time constant enlargement effect. Roll–off effect of each OTA transconductance
as well as each CCII current transfer constant also has a devastating impact on the
desired state attractor.
Since chaotic solution is usually surrounded in hyperspace of internal system
parameters by unbounded solution strange attractor often collapses into large limit
cycle with squared quasi–radius defined by the saturation levels of the used active
141
devices.
This part deals with the study of influences of input and output parasitic properties of used real active elements. It is very interesting thing, because chaos systems
are very sensitive on initial condition and values of circuit elements which should be
kept very precisely. From this point of view it is very important to deal with question,
whether parasitic properties are critical for system function and how global behavior
changes with some sort of uncertainty. The question is whether or not these parasitic
elements can cause significant problems in formation of the state space and chaos
destruction in the worst case. The impact of the parasitic properties is to be taken
into account during the system design. Performances of the proposed circuits from
previous chapters are confirmed through numerical analysis and PSpice simulations
with consideration influence of parasitic properties of active elements. This part also
deals with mathematical analysis and calculations of eigenvalues with thinking of
influences of active elements parasitics.
6.1
Influences of Active Elements Parasitics
Non–ideal active elements are depicted in Fig. 6.1 resp. Fig. 6.2. Parasitic analysis
deals mainly with input and output properties of used active element that cause
significant problems in the state space. Important parasitic admittances of the circuit
(signed as 𝑌𝑝 ) are caused by the real input and output properties of used active
elements. Common input and output small signal parameters for OTA (OPA860) are
𝑅𝑖𝑛_𝑂𝑇 𝐴 = 455 𝑘Ω, 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴 = 54 𝑘Ω, 𝐶𝑖𝑛_𝑂𝑇 𝐴 = 2.2 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 = 2 𝑝𝐹 , for OTA
(AD844) are 𝑅𝑖𝑛_𝑂𝑇 𝐴 = 10 𝑀 Ω, 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴 = 3 𝑀 Ω, 𝐶𝑖𝑛_𝑂𝑇 𝐴 = 2 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 =
4.5𝑝𝐹 and for MO-OTA (MAX435) are 𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 = 800𝑘Ω, 𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 = 3.5𝑘Ω,
𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 = 4 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 = 4.1 𝑝𝐹 .
I0
Ii
Rin_OTA gmVi
Vi
Cin_OTA
Rout_OTA
Cout_OTA
Fig. 6.1: Non-ideal model of operational transconductance amplifier (OTA).
142
+I0
Ii
Vi
Cin_MOOT A
Rout_MOOT A gmVi
Rout_MOOT A
Cout_MOOT A
-I0
-gmVi
Rout_MOOT A
Cout_MOOT A
Fig. 6.2: Non-ideal model of multiple output operational transconductance amplifier
(MO-OTA).
6.2
Influence of Parasitic Properties of Active Elements in Circuit Based on Inertia Neuron Model
In this section are discussed influences of parasitic properties of active elements
in system based on inertia neuron model described in the previous subchapter
section 4.3. We suppose three locations (input and output admittances in three nodes) where is the highest impact of parasitic properties. These parasitic admittances
are described by a following set of the equations
𝑌𝑝1 (𝑠) = 𝐺𝑝1 + 𝑠𝐶𝑝1 ,
(6.1)
𝑌𝑝2 (𝑠) = 𝐺𝑝2 + 𝑠𝐶𝑝2 ,
(6.2)
𝑌𝑝3 (𝑠) = 𝐺𝑝3 + 𝑠𝐶𝑝3 .
(6.3)
The relations between inertia neuron model and parasitic admittances are given by
the formulas
1
−(𝐶1 + 𝐶𝑝1 ) 𝑑𝑢
= 𝑢2 + 𝑎𝑢1 2 − 𝑢1 2 − 𝑢3 + 𝐼 − 𝐺𝑝1 𝑢1
𝑑𝑡
2
−(𝐶2 + 𝐶𝑝2 ) 𝑑𝑢
= 1 − 𝐷𝑢1 2 − 𝑢2 − 𝐺𝑝2 𝑢2
𝑑𝑡
(6.4)
3
−(𝐶3 + 𝐶𝑝3 ) 𝑑𝑢
= 𝜇 (𝑏 (𝑢1 − 𝑥0 ) − 𝑢3 ) − 𝐺𝑝3 𝑢3 .
𝑑𝑡
1
− 𝑑𝑢
=
𝑑𝑡
𝑢2 +𝑎𝑢1 2 −𝑢1 2 −𝑢3 +𝐼−𝐺𝑝1 𝑢1
𝐶1 +𝐶𝑝1
2
− 𝑑𝑢
=
𝑑𝑡
3
− 𝑑𝑢
=
𝑑𝑡
1−𝐷𝑢1 2 −𝑢2 −𝐺𝑝2 𝑢2
𝐶2 +𝐶𝑝2
𝜇(𝑏(𝑢1 −𝑥0 )−𝑢3 )−𝐺𝑝3 𝑢3
,
𝐶3 +𝐶𝑝3
143
(6.5)
Fig. 6.3: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝2 .
Fig. 6.4: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝3 .
Fig. 6.5: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝3 .
Fig. 6.6: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥
as a function of 𝐺𝑝1 and 𝐺𝑝2 .
Fig. 6.7: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥
as a function of 𝐺𝑝1 and 𝐺𝑝3 .
Fig. 6.8: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥
as a function of 𝐺𝑝2 and 𝐺𝑝3 .
144
As was mentioned in the previous subchapter (1.2.1) to obtain sensitivity to the
initial conditions (chaos) it is necessary to have one LE positive. From the viewpoint
of chaos destruction has been calculated the largest Lyapunov exponents (𝐿𝐸𝑚𝑎𝑥 )
which are indicated the possible occurance of chaos. Working capacitances were set
on the normative value equal to 1. The positive 𝐿𝐸𝑚𝑎𝑥 dependence on values of
parasitic properties are shown in Fig. 6.3 to Fig. 6.8 using the 3D contour plot with
scale 𝐿𝐸𝑚𝑎𝑥 ∈ (−0.01, 0.01). Although full graph should be many–dimensional only
two nonidealities are considered for each graph. This contour plots of the 𝐿𝐸𝑚𝑎𝑥
have the axis resolution 𝑋 = 𝑌 = 30 values uncovering how the structure of the
chaotic attractor is sensitive to the changes of parasitic properties. The numerical
analysis involving the computation of the 𝐿𝐸𝑚𝑎𝑥 reveals that the chaotic regions
are significantly surrounded by the regions with unbounded solution. If the parasitic
properties are growing up the 𝐿𝐸𝑚𝑎𝑥 becomes negative. It is indicating the impossible occurance of chaos for this interval of parameters. Therefore it is evident that
the most common solution of the system with influence of parasitic properties is a
limit cycle. On the other side when the values of parasitic properties convert to zero
the positive value of 𝐿𝐸𝑚𝑎𝑥 is indicating the possible occurance of chaos.
145
6.3
Influence of Parasitic Properties of Active Elements in Circuit Based on Memristor Properties
In Fig. 6.1 the suitable model of the real OTA which includes the most important
parasitic parameters is given. Then using this model (Fig. 6.1) the circuit diagram
from Fig. 4.64 can be supplemented as shown in Fig. 6.9 to include all parasitic
influences. Elementswith crosshatch pattern are representing parasitic influences.
We suppose three locations (input and output admittances in three nodes) where is
the highest impact of parasitic properties. These parasitic admittances (see Fig. 6.9)
are expressed
ISET1
ISET3
gm1
gm3
ISET2
gm2
X1
X2
Y1
Y2
Z
X
C1
W
X1
X2
Y1
Y2
Z
R1
R2
W
Y
Gp1
C2
Z
Gp2
Gp3
R3
C3
Fig. 6.9: Circuit realization of the chaotic system with influence of parasitic properties of active elements.
𝑌𝑝1 (𝑠) = 𝐺𝑝1 + 𝑠𝐶𝑝1 = (𝐺𝑝𝑖𝑛2 + 𝐺𝑝𝑜𝑢𝑡3 )+
=
1
𝑅𝑖𝑛_𝑂𝑇 𝐴2
+ 𝑠(𝐶𝑝𝑖𝑛1 + 𝐶𝑝𝑜𝑢𝑡3 ) =
1
+
+ 𝑠 (𝐶𝑖𝑛_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 ) ,
𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴
146
(6.6)
𝑌𝑝2 (𝑠) = 𝐺𝑝2 + 𝑠𝐶𝑝2 = (𝐺𝑝𝑖𝑛1 + 𝐺𝑝𝑖𝑛3 + 𝐺𝑝𝑜𝑢𝑡1 + 𝐺𝑝𝑜𝑢𝑡2 )
+ 𝑠(𝐶𝑝𝑖𝑛1 + 𝐶𝑝𝑖𝑛3 + 𝐶𝑝𝑜𝑢𝑡1 + 𝐶𝑝𝑜𝑢𝑡2 ) =
1
1
1
1
+
+
+
+
=
𝑅𝑖𝑛_𝑂𝑇 𝐴1 𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴1 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴2
(6.7)
+ 𝑠(𝐶𝑖𝑛_𝑂𝑇 𝐴1 + 𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴2 ),
𝑌𝑝3 (𝑠) = 𝐺𝑝3 + 𝑠𝐶𝑝3 = 𝐺𝑝𝑜𝑢𝑡3 + 𝑠𝐶𝑝𝑜𝑢𝑡3 =
1
=
+ 𝑠𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 .
𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴
(6.8)
The relations between ideal model and parasitic admittances are given by the formulas
1
−(𝐶1 + 𝐶𝑝1 ) 𝑑𝑢
= 𝐺𝑝1 𝑢1 − 𝑔𝑚3 𝑢2
𝑑𝑡
2
−(𝐶2 + 𝐶𝑝2 ) 𝑑𝑢
= 13 𝑔𝑚2 𝑢1 − ( 12 𝑔𝑚1 − 𝐺𝑝2 )𝑢2 + 12 𝑢2 𝑢3 2
𝑑𝑡
(6.9)
3
= 𝑔𝑚3 𝑢2 + (𝐺 + 𝐺𝑝3 )𝑢3 − 𝑢2 𝑢3
−(𝐶3 + 𝐶𝑝3 ) 𝑑𝑢
𝑑𝑡
1
=
− 𝑑𝑢
𝑑𝑡
2
− 𝑑𝑢
=
𝑑𝑡
1
𝑔 𝑢 −( 12 𝑔𝑚1 −𝐺𝑝2 )𝑢2 + 12 𝑢2 𝑢3 2
3 𝑚2 1
𝐶2 +𝐶𝑝2
3
− 𝑑𝑢
=
𝑑𝑡
𝐺𝑝1 =
𝐺𝑝2 =
1
𝑅𝑖𝑛_𝑂𝑇 𝐴2
1
+
𝑅𝑖𝑛_𝑂𝑇 𝐴1
𝐺𝑝1 𝑢1 −𝑔𝑚3 𝑢2
𝐶1 +𝐶𝑝1
+
(6.10)
𝑔𝑚3 𝑢2 +(𝐺+𝐺𝑝3 )𝑢3 −𝑢2 𝑢3
𝐶3 +𝐶𝑝3
1
𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴
1
+
𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴
, 𝐺𝑝3 =
1
𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴
1
1
+
𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴1 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴2
(6.11)
(6.12)
𝐶𝑝1 = 𝐶𝑖𝑛_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 , 𝐶𝑝3 = 𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴
(6.13)
𝐶𝑝2 = 𝐶𝑖𝑛_𝑂𝑇 𝐴1 + 𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴2
(6.14)
The concrete values of the parasitic admitances of the developed circuitry shown in
Fig. 6.9 are for OTA (OPA860) 𝑅𝑖𝑛_𝑂𝑇 𝐴 = 455 𝑘Ω, 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴 = 54 𝑘Ω, 𝐶𝑖𝑛_𝑂𝑇 𝐴 =
2.2 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 = 2 𝑝𝐹 and for MO-OTA (MAX435) are 𝑅𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 = 800 𝑘Ω,
𝑅𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 = 3.5 𝑘Ω, 𝐶𝑖𝑛_𝑀 𝑂𝑂𝑇 𝐴 = 4 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑀 𝑂𝑂𝑇 𝐴 = 4.1 𝑝𝐹 . Results of numerical analysis with influence of parasitic elements are shown in Fig. 6.10. The
positive 𝐿𝐸𝑚𝑎𝑥 dependence on values of parasitic properties are shown in Fig. 6.11
147
Fig. 6.10: Numerical analysis of system with memristor properties and influence of
parasitic elements - projection X-Y (red-with parasitic, blue-without parasitic).
to Fig. 6.18 with scale 𝐿𝐸𝑚𝑎𝑥 ∈ (0, 0.04). Capacitances 𝐶1 , = 𝐶2 , = 𝐶3 used in
numerical analysis have normative values 1. Contour plots of the 𝐿𝐸𝑚𝑎𝑥 have the
axis resolution 𝑋 = 𝑌 = 30 values. As is evident from plots Fig. 6.11 to Fig. 6.18
circuitry is much more sensitive to the changes of the parasitic conductances than
the parasitic capacitances. The influence of the parasitic capacitance will be applied
in cases when their value will be close to the value of working capacitances. The
conclusion is that at high frequencies, the values of the parasitic capacitances are
comparable to those of other circuit elements and thus the resulted behavior of the
circuit is unpredictable.
0.04
0.04
LEmax
LEmax
0.03
0.03
0.02
0.02
0.01
0.01
0
0.1
0.05
0.05
GoutOTA
0.1
0.1
0
0
0
0
GinOTA
GoutMOTA
Fig. 6.11: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of OPA860 parasitic conductance.
0.05
0.2
0.1
0.3
0.15
GinMOTA
Fig. 6.12: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of MAX435 parasitic conductance.
148
0.04
0.04
LEmax
LEmax
0.03
0.03
0.02
0.02
0.01
0.01
0
0
0
0
0.05
GinMOTA
0.2
0.1
0.1
0.15 0.1
0
0
0.1
0.05
GinOTA
0.2
0.1
GoutMOTA0.2
Fig. 6.13: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of OPA860 and MAX435
input parasitic conductances.
0.1
0.3
0.1
0.05
GoutOTA
Fig. 6.14: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of OPA860 and MAX435
output parasitic conductances.
0.04
0.04
LEmax
LEmax
0.03
0.02
0.02
0.01
0
0
CoutOTA
1
1
0.5
0.5
0.5
0.5
1
1
CoutMOTA
CinOTA
Fig. 6.15: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of OPA860 parasitic capacitance.
1.5
2
2
CinMOTA
1.5
Fig. 6.16: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of MAX435 parasitic capacitance.
0.04
0.04
LEmax
LEmax
0.03
0.02
0.02
0.01
0
0
0.5
0.5
1.5
2
2
1.5
0.5
1
1
1
CinMOTA
CoutMOTA
CinOTA
Fig. 6.17: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of OPA860 and MAX435
input parasitic capacitances.
1
2
3
2
1.5
CoutOTA
Fig. 6.18: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of OPA860 and MAX435
output parasitic capacitances.
149
6.3.1
Calculation of Eigenvalues
Now we will consider a new form of the system (6.9), where state matrix 𝐴𝑝 is
represented influence of the parasitic conductances of the active elements.
(︁
ẋ = (A + A𝑝 ) 𝑥 + B𝑥𝑥𝑇 C + D𝑥 𝑥𝑇 C
⎛
0
⎜
1
⎜
A = ⎝ − 3 · 𝑔𝑚2
0
)︁2
(6.15)
⎞
𝑔𝑚3
0
⎟
1
· 𝑔𝑚1
0 ⎟
⎠,
2
−𝑔𝑚3 −0.6
⎛
(6.16)
⎞
−𝐺𝑝1
0
0
⎜
⎟
⎜
A𝑝 = ⎝ 0
−𝐺𝑝2
0 ⎟
⎠,
0
0
−𝐺𝑝3
⎛
⎞
⎛
(6.17)
⎞
0 0 0
0
⎜
⎟
⎜
⎟
⎟
⎜
⎟
B=⎜
⎝ 0 0 0 ⎠, C = ⎝ 0 ⎠
0 1 0
1
⎛
(6.18)
⎞
0 0 0
⎜
⎟
1
⎟
D=⎜
⎝ 0 −2 0 ⎠ ,
0 0 0
(6.19)
The Jacobian matrix and the local behavior of the system (6.10) near the origin
with influence of parasitic properties of active elements is
⎛
⎞
−𝐺𝑝1
1
0
⎜
⎟
1
⎟
J𝑝 = ⎜
− 12 𝑧 2 + 21 − 𝐺𝑝2
−𝑦𝑧
⎝ −3
⎠
0
𝑧−1
𝑦 − 0.6 − 𝐺𝑝3
(6.20)
and characteristic polynomial for critical point (0, 0, 0) is following
𝑑𝑒𝑡(𝜆I − J𝑝 ) =
= 𝜆3 + 1.714𝜆2 + 1.223𝜆 + 0.433 = 0.
(6.21)
New values of eigenvalues are
𝜆4,5 = 0.086 ± 0.44𝑖
150
𝜆6 = −0.886.
(6.22)
6.4
Influence of Parasitic Properties of Active Elements in Circuit Based on Sprott system
Consider same algebraically simple three-dimensional ODEs with six terms and one
nonlinearity (4.29) as was mentioned in subchapter section 4.5. In Fig. 6.1, resp.
Fig. 6.2 the suitable models of the real OTA and MO-OTA which includes the most
important parasitic parameters are given. Then using this model (Fig. 6.1, Fig. 6.2)
the circuit diagram from Fig. 4.34 can be supplemented as shown in Fig. 6.19 to
include all parasitic influences. Elementswith crosshatch pattern are representing
parasitic influences. In circuit realization (Fig. 6.19) we suppose four locations (two
nodes and two input diferences admittance) where parasitics cause the highest impact. These parasitic admittances can be expressed as
gm3
Yp3
x.z
Yp4
gm2
gm1
Y
X
C1
Yp1
C2
Z
G
Yp2
C3
Fig. 6.19: Schematic of circuit realization with important parasitic influences.
𝑌𝑝1 (𝑠) = 𝐺𝑝1 + 𝑠𝐶𝑝1 = (𝐺𝑝𝑖𝑛1 + 𝐺𝑝𝑜𝑢𝑡1 +
+ 𝐺𝑝𝑜𝑢𝑡3 ) + 𝑠(𝐶𝑝𝑖𝑛1 + 𝐶𝑝𝑜𝑢𝑡1 + 𝐶𝑝𝑜𝑢𝑡3 ) =
1
1
1
=
+
+
+
𝑅𝑖𝑛_𝑂𝑇 𝐴1 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴1 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴3
(6.23)
+ 𝑠 (𝐶𝑖𝑛_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴1 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴3 )
𝑌𝑝2 (𝑠) = 𝐺𝑝2 + 𝑠𝐶𝑝2 = 𝐺𝑝𝑜𝑢𝑡2 + 𝑠𝐶𝑝𝑜𝑢𝑡2 =
1
=
+ 𝑠𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴2
𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴2
151
(6.24)
𝑌𝑝4 (𝑠) = 𝐺𝑝4 + 𝑠𝐶𝑝𝑝4 = 𝐺𝑝𝑖𝑛2 + 𝑠𝐶𝑖𝑛2
1
+ 𝑠𝐶𝑖𝑛_𝑂𝑇 𝐴3
𝑅𝑖𝑛_𝑂𝑇 𝐴3
1
=
+ 𝑠𝐶𝑖𝑛_𝑂𝑇 𝐴2
𝑅𝑖𝑛_𝑂𝑇 𝐴2
𝑌𝑝3 (𝑠) = 𝐺𝑝3 + 𝑠𝐶𝑝𝑝3 = 𝐺𝑝𝑖𝑛3 + 𝑠𝐶𝑖𝑛3 =
(6.25)
(6.26)
𝑑𝑢1
= (𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1 + 𝐺𝑝4 𝑢2 + (𝑔𝑚3 + 𝐺𝑝3 )𝑢3 −
𝑑𝑡
𝑑𝑢3
𝑑𝑢1
𝑑𝑢2
𝑑𝑢1
− 𝐶𝑝𝑝3
+ 𝐶𝑝𝑝3
− 𝐶𝑝𝑝4
+ 𝐶𝑝𝑝4
𝑑𝑡
𝑑𝑡
𝑑𝑡
𝑑𝑡
𝑑𝑢2
𝑑𝑢2
𝑑𝑢1
−𝐶2
= 𝐺𝑝4 𝑢1 − (𝐺 + 𝐺𝑝4 )𝑢2 + 𝑢1 𝑢3 + 𝐶𝑝𝑝4
− 𝐶𝑝𝑝4
𝑑𝑡
𝑑𝑡
𝑑𝑡
𝑑𝑢3
𝑑𝑢1
−(𝐶3 + 𝐶𝑝2 )
= (−𝑔𝑚2 + 𝐺𝑝3 )𝑢1 + 𝑔𝑚2 𝑢2 − (𝐺𝑝2 + 𝐺𝑝3 )𝑢3 − 𝐶𝑝𝑝3
+
𝑑𝑡
𝑑𝑡
𝑑𝑢3
+ 𝐶𝑝𝑝3
𝑑𝑡
(6.27)
−(𝐶1 + 𝐶𝑝1 )
𝑑𝑢1
(𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1 𝐶𝑝𝑝3 (−𝑔𝑚2 + 𝐺𝑝3 )𝑢1
=
+
+
𝑑𝑡
𝐶1 + 𝐶𝑝1
𝐶3 + 𝐶𝑝2
𝐶𝑝𝑝3 (𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1 𝐶𝑝𝑝4 𝐺𝑝4 𝑢1
−
+
+
𝐶1 + 𝐶𝑝1
𝐶2
𝐶𝑝𝑝4 (𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1
𝐺𝑝4 𝑢2
𝐶𝑝𝑝3 𝑔𝑚2 𝑢2
+
+
−
+
𝐶1 + 𝐶𝑝1
𝐶1 + 𝐶𝑝1
𝐶3 + 𝐶𝑝2
𝐶𝑝𝑝3 𝐺𝑝4 𝑢2 𝐶𝑝𝑝4 (𝐺 + 𝐺𝑝4 )𝑢2 𝐶𝑝𝑝4 𝐺𝑝4 𝑢2 (𝑔𝑚3 + 𝐺𝑝3 )𝑢3
+
+
+
+
+
𝐶1 + 𝐶𝑝1
𝐶2
𝐶1 + 𝐶𝑝1
𝐶1 + 𝐶𝑝1
𝐶𝑝𝑝3 (𝐺𝑝2 + 𝐺𝑝3 )𝑢3 𝐶𝑝𝑝3 (𝑔𝑚3 + 𝐺𝑝3 )𝑢3 𝐶𝑝𝑝4 (𝑔𝑚3 + 𝐺𝑝3 )𝑢3 𝐶𝑝𝑝4 𝑢1 𝑢3
+
+
+
−
𝐶3 + 𝐶𝑝2
𝐶1 + 𝐶𝑝1
𝐶1 + 𝐶𝑝1
𝐶2
𝑑𝑢2
𝐺𝑝4 𝑢1 𝐶𝑝𝑝4 𝐺𝑝4 𝑢1 𝐶𝑝𝑝4 (𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1
−
=
−
−
−
𝑑𝑡
𝐶2
𝐶2
𝐶1 + 𝐶𝑝1
(𝐺 + 𝐺𝑝4 )𝑢2 𝐶𝑝𝑝4 (𝐺 + 𝐺𝑝4 )𝑢2 𝐶𝑝𝑝4 𝐺𝑝4 𝑢2 𝐶𝑝𝑝4 (𝑔𝑚3 + 𝐺𝑝3 )𝑢3
−
−
−
−
+
𝐶2
𝐶2
𝐶1 + 𝐶𝑝1
𝐶1 + 𝐶𝑝1
𝑢1 𝑢3 𝐶𝑝𝑝4 𝑢1 𝑢3
+
+
𝐶2
𝐶2
(−𝑔𝑚2 + 𝐺𝑝3 )𝑢1 𝐶𝑝𝑝3 (𝑔𝑚1 − 𝑔𝑚3 − 𝐺𝑝1 − 𝐺𝑝3 − 𝐺𝑝4 )𝑢1
𝑑𝑢3
−
=
+
−
𝑑𝑡
𝐶3 + 𝐶𝑝2
𝐶1 + 𝐶𝑝1
𝐶𝑝𝑝3 (−𝑔𝑚2 + 𝐺𝑝3 )𝑢1
𝑔𝑚2 𝑢2
𝐶𝑝𝑝3 𝐺𝑝4 𝑢2 𝐶𝑝𝑝3 𝑔𝑚2 𝑢2
−
+
+
−
−
𝐶3 + 𝐶𝑝2
𝐶3 + 𝐶𝑝2
𝐶1 + 𝐶𝑝1
𝐶3 + 𝐶𝑝2
(𝐺𝑝2 + 𝐺𝑝3 )𝑢3 𝐶𝑝𝑝3 (𝐺𝑝2 + 𝐺𝑝3 )𝑢3 𝐶𝑝𝑝3 (𝑔𝑚3 + 𝐺𝑝3 )𝑢3
−
+
+
𝐶3 + 𝐶𝑝2
𝐶3 + 𝐶𝑝2
𝐶1 + 𝐶𝑝1
(6.28)
−
The concrete values of the parasitic admitances of the developed circuitry shown
in Fig. 6.19 are for OTA (OPA860) 𝑅𝑖𝑛_𝑂𝑇 𝐴 = 455𝑘Ω, 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴 = 54𝑘Ω, 𝐶𝑖𝑛_𝑂𝑇 𝐴 =
2.2 𝑝𝐹 , 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 = 2 𝑝𝐹 .
152
Fig. 6.20: Numerical analysis with influence of parasitic elements - projection X-Y
(red - with parasitic, blue - without parasitic).
𝐺𝑝1 =
𝐺𝑝2
1
1
+
+
1
𝑅𝑖𝑛_𝑂𝑇 𝐴 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴 𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴
1
1
1
=
, 𝐺𝑝3 =
, 𝐺𝑝4 =
𝑅𝑜𝑢𝑡_𝑂𝑇 𝐴
𝑅𝑖𝑛_𝑂𝑇 𝐴
𝑅𝑖𝑛_𝑂𝑇 𝐴
(6.29)
(6.30)
𝐶𝑝1 = 𝐶𝑖𝑛_𝑂𝑇 𝐴 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 + 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴
(6.31)
𝐶𝑝2 = 𝐶𝑜𝑢𝑡_𝑂𝑇 𝐴 , 𝐶𝑝𝑝3 = 𝐶𝑖𝑛_𝑂𝑇 𝐴 , 𝐶𝑝𝑝4 = 𝐶𝑖𝑛_𝑂𝑇 𝐴
(6.32)
Values of used passive elements in schematic in Fig. 6.19 were chosen same as in
previous chapter (𝐶1 = 𝐶2 = 𝐶3 = 470 𝑛𝐹, 𝑅 = 1 𝑘Ω). Results of numerical analysis
with influence of parasitic elements are shown in Fig. 6.20. Influences of parasitic
properties were simulated also in PSpice and the results of the simulations are shown
in Fig. 6.21. The positive 𝐿𝐸𝑚𝑎𝑥 dependence on values of parasitic properties are
shown in Fig. 6.22 to Fig. 6.37 with scale 𝐿𝐸𝑚𝑎𝑥 ∈ (0, 0.01). Capacitances 𝐶1 , =
𝐶2 , = 𝐶3 used in numerical analysis have again normative values 1. Contour plots
of the 𝐿𝐸𝑚𝑎𝑥 have the axis resolution 𝑋 = 𝑌 = 30 values. Circuit has the similar
properties as in previuous case with memristor properties. Sensitivity to change of
the parasitic conductances is bigger than the sensitivity to the changes of parasitic
capacitances. The most critical to chaos destruction seems to be parasitic output
resistance of the MO-OTA element MAX435 with value approaching the working
resistance.
153
2.0V
2.0V
1.0V
1.0V
0V
0V
-1.0V
-1.0V
-2.0V
-2.0V
-3.0V
-3.0V
V(x)
-2.0V
-1.0V
0V
1.0V
2.0V
3.0V
-3.0V
-3.0V
V(x)
-V(z)
-2.0V
-1.0V
0V
1.0V
2.0V
3.0V
-V(z)
Fig. 6.21: Circuit simulation with influence of parasitic elements (left - with parasitic,
right - with parasitic compensate ).
Fig. 6.22: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝2 .
Fig. 6.23: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝𝑝3 .
Fig. 6.24: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝1 and 𝐶𝑝𝑝4 .
Fig. 6.25: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝𝑝3 .
154
Fig. 6.26: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝2 and 𝐶𝑝𝑝4 .
Fig. 6.27: Influence of parasitic capacitances on the size of the 𝐿𝐸𝑚𝑎𝑥 as a
function of 𝐶𝑝𝑝3 and 𝐶𝑝𝑝4 .
Fig. 6.28: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝1 and 𝐺𝑝2 .
Fig. 6.29: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝1 and 𝐺𝑝3 .
Fig. 6.30: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝1 and 𝐺𝑝4 .
Fig. 6.31: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝2 and 𝐺𝑝3 .
155
Fig. 6.32: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝2 and 𝐺𝑝4 .
Fig. 6.33: Influence of parasitic conductances on the size of the 𝐿𝐸𝑚𝑎𝑥 as
a function of 𝐺𝑝3 and 𝐺𝑝4 .
Fig. 6.34: Influence of parasitic conductance and capacitance on the size
of the 𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝1 and
𝐶𝑝1 .
Fig. 6.35: Influence of parasitic conductance and capacitance on the size
of the 𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝2 and
𝐶𝑝2 .
Fig. 6.36: Influence of parasitic conductance and capacitance on the size
of the 𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝3 and
𝐶𝑝𝑝3 .
Fig. 6.37: Influence of parasitic conductance and capacitance on the size
of the 𝐿𝐸𝑚𝑎𝑥 as a function of 𝐺𝑝4 and
𝐶𝑝𝑝4 .
156
6.4.1
Calculation of Eigenvalues
Now focus attention on the calculation of the system eigenvalues with respect to
parasitic properties of active elements. State matrices A1𝑝 , A1𝑝 , A1𝑝 are represented
influence of the parasitic admittances of the active elements.
ẋ = (A + A1𝑝 + A2𝑝 + A3𝑝 ) x + Bxx𝑇 C
⎛
⎞
0.36 · (𝑔𝑚1 − 𝑔𝑚3 ) 0 𝑔𝑚3
⎜
⎟
A=⎜
0
−𝐺 0 ⎟
⎝
⎠
𝑔𝑚2
𝑔𝑚2 0
⎛
⎞
⎛
−𝐺𝑝1 0
0
⎟
⎜
=⎜
0
0
0 ⎟
⎠
⎝
0
0 −𝐺𝑝2
(6.36)
⎞
⎛
−𝐺𝑝3 0 𝐺𝑝3
⎟
⎜
⎜
=⎝ 0
0
0 ⎟
⎠
𝐺𝑝3 0 −𝐺𝑝3
(6.37)
⎞
⎛
A3𝑝
(6.35)
⎞
⎛
A2𝑝
(6.34)
⎞
0 0 0
0
⎜
⎟
⎜
⎟
⎟
⎜
⎟
B=⎜
⎝ 1 0 0 ⎠ C=⎝ 0 ⎠
0 0 0
1
A1𝑝
(6.33)
−𝐺𝑝4 𝐺𝑝4 0
⎟
⎜
⎜
= ⎝ 𝐺𝑝4 −𝐺𝑝4 0 ⎟
⎠
0
0
0
(6.38)
The Jacobian matrix and the local behavior of the system (6.33) near the origin
with influence of parasitic properties of active elements is
⎛
⎞
0.31637 0.0022
1.0022
⎜
⎟
⎜
⎟
J𝑝 = ⎝
𝑧
−1.0022
𝑥
⎠
−0.9978
1
−0.0207
(6.39)
Characteristic polynomial for critical point (0, 0, 0) is
𝑑𝑒𝑡(𝜆I − J𝑝 ) =
= 𝜆3 + 0.707𝜆2 + 0.697𝜆 + 0.993 = 0,
(6.40)
and for critical point (−2.5, −2.5, 1) is following
𝑑𝑒𝑡(𝜆I − J𝑝 ) =
= 𝜆3 + 0.707𝜆2 + 3.195𝜆 + 0.805 = 0.
157
(6.41)
From the characteristic equation (6.40, 6.41) we can determine the eigenvalues of
system with parasitic properties in the following form
𝜆1,2 = 0.21 ± 0.978𝑖
𝜆4,5 = −0.446 ± 1.778𝑖
158
𝜆3 = −1.
(6.42)
𝜆6 = 0.236.
(6.43)
6.5
Summary
In this chapter, three types of circuitry realization in which cases the influence of
parasitic properties of used active elements to shape of the desired strange attractors
were described. Namely circuit based on inertia neuron model, circuit based on
memristor properties and circuit based on Sprott system were considered.
We presented here also a numerical analysis of systems with influence of parasitic admitances. Experiments suggest that systems are much more sensitive to the
changes of the parasitic conductances than the parasitic capacitances. The common
situation is that nonzero input or output admittance increase dynamical flow dissipativity. Another conclusion is that influence of the parasitic capacitance will be
applied in cases when their value will be close to the value of working capacitances. At high frequencies, the values of the parasitic capacitances are comparable to
functional ones and thus the resulting behavior of the circuit is unpredictable and
can lead to chaos destruction (from geometrical sesne).
Other crux of this section is in calculations of eigenvalues with respect to influence
of parasitic properties of active elements.
The possibility of chaos destruction via parasitic properties of the used active
elements were described, deeply discussed and published in[208, 210].
159
7
CONCLUSION
In this doctoral thesis we have proposed several types of electronically adjustable
oscillators, autonomous and nonautonomous chaotic systems, different possibilities
towards analog–digital synthesis and influence of parasitic properties of used active
elements on structural stability of prescribed geometrical structure of strange attractor. By referring to the best knowledge of the author, circuitry implementations
and in this doctoral thesis were not so far reported.
Several novel active elements with adjustable fundamental properties (current
and voltage gain) were discussed in this thesis. First of them is very simple electronically adjustable oscillator employing only two active devices (CCII–) and in the
extreme only two passive elements (capacitors). It allows electronic tuning of the oscillation frequency and condition of oscillation by DC driving voltage. It was practically tested from 320 𝑘𝐻𝑧 to 1.75 𝑀 𝐻𝑧. Under certain conditions (limited range),
the harmonic distortion can be achieved below 1% and the separation of the higher
harmonics more then 50𝑑𝐵 [221]. However there are some drawbacks of this solution.
The equation for oscillation frequency (3.9) is not very suitable and therefore tuning
is possible only in a limited range. The network was verified without the subcircuit
for amplitude stabilization (only by nonlinear limitation of used active elements).
Therefore practically available range of tuning with achievable low THD is limited.
For invariable level of output signal very small changes of 𝐵1 are necessary. The
first conception of the oscillator where CC1 has a fixed gain is not suitable because
the control of the condition of oscillation is not possible. Operation of the proposed
oscillator was verified through simulations and measurements of the real circuit in
the frequency range of units MHz. Also important parasitic effects in this circuit
were discussed in detail.
Other types are three modified oscillator conceptions that are quite simple, directly electronically adjustable, providing independent control of oscillation condition and frequency in 3R-2C oscillator. The most important contributions of presented solutions are direct electronic and also independent control of CO and 𝑓0 , suitable AGC circuit implementation, buffered low–impedance outputs, and of course,
grounded capacitors [222]. Independent tunability by only one parameter is very
useful, but tuning characteristic is nonlinear. The most important drawback is dependence of amplitude 𝑉𝑂𝑈 𝑇 1 on current gain 𝐵1 . Circuit in Fig. 3.19 was selected
in order to show all features and document the expected behavior, which was first
derived theoretically (equations). It is quite hidden problem at first sight without
precise analyses. This problem was solved and possible conception (Fig. 3.20) was
introduced. It is necessary to change oscillation frequency simultaneously by two parameters (adjustable current gains) and oscillation condition by adjustable voltage
160
gain (all in frame of two active elements). Equality (and invariability) of generated amplitudes and linearity of tuning characteristic during the tuning process are
required aspects. This feature is not novel advantage of circuit in Fig. 3.20. Detailed
discussion is available in [14] for example.
Last type is new oscillator suitable for quadrature and multiphase signal generation. Active element, which was defined quite recently i.e. controlled gain-current
follower differential output buffered amplifier (CG-CFDOBA) [15, 16], and newly
introduced element so–called controlled gain–buffered current and voltage amplifier
(CG-BCVA) were used for purposes of oscillator synthesis. Electronic control of two
parameters in frame of one active element is quite attractive method, which is very
useful in particular applications. Presented methods of gain control allow synthesis
and design of electronically controllable application (oscillator in our case) quite
easily and with very favorable features. Main highlighted benefits can be found in
electronic linear control of oscillation frequency (tested from 0.25 𝑀 𝐻𝑧 to 8 𝑀 𝐻𝑧)
and electronic control of oscillation condition. The output levels were almost constant during the tuning process and reached about 200 𝑚𝑉𝑃 −𝑃 . THD below 0.5%
in range above 2 𝑀 𝐻𝑧 was achieved [224]. In comparison to some previously reported types [76, 154, 222, 223] dependence of output amplitudes on tuning process
was eliminated by simultaneous adjusting of both time constants of integrators [14].
Grounded capacitors are common requirement in similar types of circuits. Precise
analysis of real parameters and nonidealities of active elements allows determining
of more accurate description and simulations. Operation of the proposed oscillators were verified through simulations and measurements of the real circuits and
published in[221, 222, 224].
In the second chapter, circuitry implementations of interesting autonomous and
nonautonomous chaotic systems have been presented. Based on the optimized dynamical system of class C with PWL feedback, a fully analog chaotic oscillator works in
hybrid mode has been proposed for laboratory measurements [209]. This chaotic circuit is currently used for student demontrations in Department of Radio Electronics.
Main contribution is in circuitry implementation of a fully analog chaotic oscillator
with a new available active elements. The advantage is immediately evident. The
smaller number of active elements is in the whole circuit.
Fully analog circuitry implementation of the inertia neuron based on the ordinary differential equations of Hindmarsh–Rose model has been realised and published [200]. The qualitatively different behavior of HR model in time domain were
demonstrated. From experimental verification is evident that for 𝑥𝑟 = −0.6 system
exhibits spiking behavior. If we changed this bifurcation parameter to 𝑥𝑟 = −1.6
the system began to exhibit chaotic behavior (chaotic dynamics is obtained for a
small range around value 𝑥𝑟 = −1.6). With other change of 𝑥𝑟 system exhibited
161
bursting dynamics. It is evident that all the main dynamics of a neuron (spiking,
bursting and chaos) can be obtained with the proposed circuit by properly setting
the control parameters and after quite long transient behavior. It eventually turns
out that this system in not as sensitive as expected.
Other example of real chaotic system was novel circuitry implemnation of the
Nóse–Hoover thermostated dynamic system [218]. The Nóse–Hoover system has relatively many interesting limiting cycles and relatively complicated Poincare sections, but otherwise mostly reinforces the idea that small systems do not follow a
statistical-mechanical average over accessible states. On the other hand, the twodimensional calculations indicate that only slightly more complicated systems probably do fill their phase spaces in a quasiergodic way. A careful study of the two–
soft–disk system, using Nóse dynamics in a phase space with the variables, led to
no evidence for the failure of statistical mechanics. Based on this evidence we would
expect that even very simple nonequilibrium systems, or quantum systems, with
even more capability for mixing phase space, do indeed fill their phase spaces in an
ergodic way [121]. New implementations of chaotic circuits using transconductance
operational amplifiers and analog multipliers were proposed [211, 213]. We used two
systems (original and modified system) publicated by Sprott [159] and chatotic system based on memristor mathematical model published by Muthuswamy and Chua
[101] as an example of chaotic systems.
Last circuitry implementations deals with nonautonomous chaotic system based
on Ueda oscillator. First circuitry implementation works in voltage mode and second in hybrid mode [207]. Those conceptions were experimentally verified in both
time domain and frequency domain. The frequency of driven sinusoidal signal was
changed over the range 1.5 𝑘𝐻𝑧 < 𝑓 < 4 𝑘𝐻𝑧 and study development in the motion
from periodic cycle to strange attractor. The proper function of the final circuits structure has been verified by means of the PSpice simulator as well as by a
practical experiments on the real oscillators and on the breadboard. Many simulations and laboratory experiments proved a good agreement between numerical
integration, practical simulation and measurement. The exponential divergence of
trajectories that underlies chaotic behavior, and the resulting sensitivity to initial
conditions, lead to long–term unpredictability which manifests itself as deterministic
randomness in the time domain.
In the third chapter, the well known 2D 𝑚 𝑥 𝑛 scroll system was chosen and was
realized utilizing novel approach using the data converters as non-linear functions.
With the growing order of the system, the presence of chaotic behavior is more
probable. First the models were derived to simulate the data converters connected
directly (ADC-DAC). Than the connection was reduced to produce less scrolls. Other
crux is in the verify chaotic behavior of proposed conception. The circuit simulator
162
PSpice was used for theoretical verify and then the circuit prototype was build and
measured. The simulation results and measurements prove a good final agreement
between theory and practice and were published in[219].
In the last chapter, three types of circuitry realization in which cases the influence of parasitic properties of used active elements to shape of the desired strange
attractors were described. Namely circuit based on inertia neuron model, circuit
based on intrinsic memristor properties and circuit based on Sprott system were
considered. We presented here also a numerical analysis of systems with influence
of parasitic admitances. Experiments suggest that systems are much more sensitive
to the changes of the parasitic conductances than the parasitic capacitances. The
common situation is that nonzero input or output admittance increase dynamical
flow dissipativity. Another conclusion is that influence of the parasitic capacitance
will be applied in cases when their value will be close to the value of working capacitances. At high frequencies, the values of the parasitic capacitances are comparable
to functional ones and thus the resulting behavior of the circuit is unpredictable and
can lead to chaos destruction (from geometrical sense). Other crux of this section
is in calculations of eigenvalues with respect to influence of parasitic properties of
active elements. The possibility of chaos destruction via parasitic properties of the
used active elements were published in [208, 210].
163
REFERENCES
[1] ABUELMAATTI, M. T. Grounded capacitor current-mode oscillator using
single current follower. IEEE Transaction on circuits and systems I. 1992,
vol. 39, no. 12, p. 1018–1020.
[2] ACHO, L., VIDAL, Y. Hysteresis modeling of a class of RC-OTA hysteretic–
chaotic gGenerators. PHYSCON 2011, Leon, Spain. Sept. 2011.
[3] AHMAD, W. M. Generation and control of multi-scroll chaotic attractors in
fractional order systems. Chaos, Solution & Fractals, 2005, vol. 25, pp. 727–735.
[4] AL-RUWAIHI, K. M., Noras ,J. M. A novel linear resistor utilizing MOS transistors with identical sizes and one controlling voltage. International Journal
of Electronics. 1994, vol. 76, no. 6, p. 1083–1098.
[5] ALZAHER, H. CMOS Digitally programmable quadrature oscillators. International Journal of Circuit Theory and Applications. 2008, vol. 36, no. 8,
p. 953–966.
[6] ALZAHER, H., TASADDUG, O., AL-EES, O., AL-AMMARI, F. A complementary metal-oxide semiconductor digitally programmable current conveyor.
International Journal of Circuit Theory and Applications. 2013, vol. 41, no. 1,
p. 69–81.
[7] ALZAHER, H., TASADDUG, O. Realizations of CMOS fully differential
current followers/amplifiers. International symposium ISCAS, IEEE Press,
New York, 2009. 2009, p. 1381–1384.
[8] ARBEL, A. F., GOLDMINZ, L. Output stage for current-mode feedback amplifiers, theory and applications. Analog Integrated Circuits and Signal Processing. 1992, vol. 2, no. 3, p. 243–255.
[9] BAJER, J., BIOLEK, D. Digitally controlled quadrature oscillator employing
two ZC-CG-CDBAs. International conference Electronic Devices and Systems,
EDS09 IMPAPS CS, 2009. 2009, p. 298–303.
[10] BAO, B. C., LIU, Z., XU, J. P. Steady periodic memristor oscillator with
transient chaotic behaviours. Electronics Letters. 2010, vol. 46, no. 3, p. 237–
238.
164
[11] BARTHELEMY, H., FILLAUD, M., BOURDEL, S., GAUNERY, J. CMOS
inverters based positive type second generation current conveyors. Analog Integrated Circuits and Signal Processing. 2007, vol. 50, no. 2, p. 141–146.
[12] BHASKAR, D. R., ABDALLA, K. K., SENANI, R. CMOS Electronicallycontrolled current-mode second order sinusoidal oscillators using MO-OTAs
and grounded capacitors. Circuits and Systems 2. 2011, vol. 2, no. 2, p. 65–73.
[13] BIOLEK, Z., BIOLEK, D., BIOLKOVA, V. SPICE Model of Memristor with
Nonlinear Dopant Drift. Radioengineering. 2009, vol. 18, no. 2, p. 210–214.
[14] BIOLEK, D., LAHIRI, A., JAIKLA, W., SIRIPRUCHYANUN, M., BAJER,
J. Realisation of electronically tunable voltage–mode/current–mode quadrature sinusoidal oscillator using ZC-CG-CDBA. Microelectronics Journal. 2011,
vol. 42, no. 10, p. 1116–1123.
[15] BIOLEK, D., SENANI, R., BIOLKOVA, V., KOLKA, Z. Active elements for
analog signal processing: classification, review, and new proposal. Radioengineering. 2008, vol. 17, no. 4, p. 15–32.
[16] BIOLKOVA, V., BAJER, J., BIOLEK, D. Four-phase oscillators employing
two active elements. Radioengineering. 2011, vol. 20, no. 1, p. 334–339.
[17] BIZZARRI, F., LINARO, D., STORACE, M. PWL approximation of the
Hindmarsh-Rose neuron model in view of its circuit implementation. In Proceedings of the 18𝑡ℎ European Conference on Circuit Theory and Design. Seville,
27-30 August, 2007. Institute of Electrical and Electronics Engineers (IEEE),
2007, pp. 878 – 881. ISBN 978-1-4244-1341-6.
[18] BOYCE, W. E., DIPRIMA, R. C. Elementary differential equations and boundary value problems. Wiley, New York, 1977, 652 p., ISBN 0471093343.
[19] BROER, H. W. KAM theory: the legacy of Kolmogorov’s 1954 paper. emphBulletin of the American Mathematical Society, 2004, vol. 41, no. 4, pp. 507–
521.
[20] CAM, U., KUNTMAN, H., ACAR, C. On the realization of OTA-C oscillators.
International Journal of Electronics. 1998, vol. 85, no. 3, p. 313–326.
[21] CORINTO, F., ASCOLI, A., GILLI, M. Nonlinear dynamics of memristor
oscillators. IEEE Transactions on Circuits and Systems II: Express Briefs.
2010, vol. 57, no. 12, p. 975–979.
165
[22] DOSTAL, J. Operační zesilovače. 1. vyd. Praha: BEN 2005. 536 p. ISBN 807300-049-0
[23] DOSTAL, T. Analogové elektronické obvody. Skripta FEKT VUT v Brně, Nakladatelství VUT, Brno, 2004.
[24] DRISCOLL, T., PERSHIN, Y. V., BASOV, D. N., VENTRA, M. Chaotic
memristor. Applied Physics A. 2011, vol. 102, no. 4, p. 885–889.
[25] EGUCHI, K., INOUE, T., TSUNEDA, A. Synthesis and Analysis of a Digital Chaos Circuit Generating Multiple-Scroll Strange Attractors. IEICE
Transactions Fundamentals. 1999, vol. 82, no. 6, p. 965–972.
[26] EL-ADAWY, A., SOLIMAN, A. M., ELWAN, H O. Low voltage digitally
controlled CMOS current conveyor. International Journal of Electronics and
Communications. 2002, vol. 56, no. 3, p. 137–144.
[27] ELDBIB, I., MUSIL, V. Self-cascoded current controlled CCII based tunable
band pass filter. Proceedings of the 18𝑡ℎ International Conference Radioelektronika 2008. IEEE Press, New York. 2008. p. 1–4.
[28] ELHADJ, Z., SPROTT, J. C. Some open problems in chaos theory and dynamics. International Journal of Open Problems in Computer Science and
Mathematics, 2011, vol. 4, pp. 1-–10.
[29] ELHADJ, Z. Models and applications of chaos theory in modern sciences. CRC
Press, 2011, 742 p., ISBN 978-1578087228.
[30] FABRE, A. Third generation current conveyor: a helpful active element.
Electronics Letters. 1995, vol. 31, no. 5, p. 338–339.
[31] FABRE, A., MIMECHE, N. Class A/AB second-generation current conveyor
with controlled current gain. Electronics Letters. 1994, vol. 30, no. 16, p. 1267–
1268.
[32] FABRE, A., SAAID, O., WIEST, F., BOUCHERON, C. High frequency applications based on a new current controlled conveyor. IEEE Transaction on
Circuits and Systems - I. 1996, vol. 43, no. 2, p. 82–91.
[33] FISCHER, A. E., MONCRIEF, V. Nonautonomous dynamical systems and
the phase portrait of the reduced einstein equations. International Journal of
Modern Physics D. 2001, vol. 10, no. 6, p. 825–831, ISSN: 1793–6594.
166
[34] FITCH, A. L., IU, H. H. C., WANG, X. Y. SREERAM, V., QI, W. G. Realization of an analog model of memristor based on light dependent resistor. In
Proceedings of the IEEE International Symposium on Circuits and Systems.
2012, p. 1139–1142.
[35] FUJISAKA, H., SATO, CH. Computing the number, location, and stability
of fixed points of Poincaré maps. IEEE Transaction on CAS I: Fundamental
Theory and Applications, 1997, vol. 44, no. 4, ISSN 1057–7122.
[36] GALAN, J., CARVALAJ, R. G., TORRALBA, A., MUNOZ, F., RAMIREZANGULO, J. A low-power low-voltage OTA-C sinusoidal oscillator with large
tuning range. IEEE Transaction on Circuits and Systems - I. 2005, vol. 52,
no. 2, p. 283–291.
[37] GARCIA–LOPEZ, J. H., JAIMES–REATEGUI, R., PISARCHIK, A. N.,
MURGUIA–HERNANDEZ, A., MEDINA–GUTIERREZ, C., VALDIVIA–
HERNADEZ, R., VILLAFANA–RAUDA, E. Novel communication scheme
based on chaotic Rössler circuits. In Proceedings of the International Conference on Control and Synchronzation of Dynamical Systems. 2005, p. 276–284.
[38] GEIGER, R. L., SANCHEZ-SINENCIO, E. Active filter design using operational transconductance amplifier: a tutorial. IEEE Circuits and Devices
Magazine. 1985, p. 20–32.
[39] GUPTA, S. S., BHASKAR, D. R., SENANI, R. New voltage controlled oscillators using CFOAs. AEU - International Journal of Electronics and Communications. 2009, vol. 63, no. 3, p. 209–217.
[40] GUPTA, S. S., SENANI, R. New single resistance controlled oscillators
employing a reduced number of unity-gain cells. IEICE Electronics Express.
2004, vol. 1, no. 16, p. 507–512.
[41] GUPTA, S. S., SENANI, R. Single-resistance-controlled oscillator configurations using unity-gain cells. Analog Integrated Circuits and Signal Processing.
2006, vol. 46, no. 2, p. 111–119.
[42] GUPTA, S. S., SENANI, R. State variable synthesis of single resistance controlled grounded capacitor oscillators using only two CFOAs. IEE Proceedings
on Circuits, Devices and Systems. 1998, vol. 145, no. 2, p. 135–138.
[43] GUPTA, S. S., SENANI, R. State variable synthesis of single-resistance–
controlled grounded capacitor oscillators using only two CFOAs: additional
167
new realizations. IEE Proceedings on Circuits Devices and Systems. 1998,
vol. 145, no. 6, p. 415–418.
[44] GUPTA, S. S., SHARMA, R. K., BHASKAR, D. R., SENANI, R. Sinusoidal
oscillators with explicit current output employing current-feedback op-amps.
International Journal of Circuit Theory and Applications. 2010, vol. 38, no. 2,
p. 131–147.
[45] HE, F., RIBAS, R., LAHUEC, C., JEZEQUEL, M. Discussion on the general
oscillation startup condition and the Barkhausen criterion. Analog Integrated
Circuits and Signal Processing. 2009, vol. 59, no. 2, p. 215–221.
[46] HERENCSAR, N., LAHIRI, A., VRBA, K., KOTON, J. An electronically
tunable current–mode quadrature oscillator using PCAs. International Journal
of Electronics. 2012, vol. 99, no. 5, p. 609–621.
[47] HERENCSAR, N., VRBA, K., KOTON, J., LAHIRI, A. Realizations of
single–resistance–controlled quadrature oscillators using a generalized current
follower transconductance amplifier and a unity gain voltage–follower. International Journal of Electronics. 2010, vol. 97, no. 8, p. 879–906.
[48] HERENCSAR, N., MINAEI, S., KOTON, J., YUCE, E., VRBA, K. New
resistorless and electronically tunable realization of dual-output VM all-pass
filter using VDIBA. Analog Integrated Circuits and Signal Processing. 2013,
vol. 74, no. 1, p. 141–154.
[49] HILBORN, R. C. Chaos and nonlinear dynamics – an introduction for scientists and engineers. Oxford University Press 2000, 672 pages. ISBN 0-19850723-2.
[50] HINDMARSH, J. L., ROSE, R.M. A model of neuronal bursting using three
coupled first order differential equations. In Proceedings of the Royal Society
of London, London, 22 March, 1984. Royal Society Publishing, 1984, vol. 221,
no. 1222, pp. 87-102. ISSN 1471-2954.
[51] HIRSCH, M. W., SMALE, S. Differential equations, dynamical systems and
linear algebra. Academic Press, New York, 1974, 358 pages, ISBN 01-234-95504.
[52] HOOVER, W. G. Remark on some simple chaotic flows. Physical Review E,
1995, vol. 51, no. 1, pp. 759–760.
[53] HORNG, J. W. A sinusoidal oscillator using current–controlled current conveyors. International Journal of Electronics. 2001, vol. 88, no. 6, p. 659–664.
168
[54] CHAU, K. T., WANG, T. Chaos in electric drive systems: analysis, control
and application. Wiley, Singapore, 2011, 318 p., ISBN 978-0-470-82633-1.
[55] CHEN, J. J, CHEN, C. C, TSAO, H. W, LIU, S. I. Current–mode oscillators
using single current follower. Electronics Letters . 1991, vol. 27, no. 22, p. 2056–
2059 .
[56] CHOUDHARY, S., SLOAN, S., FOK, S., NECKAR, A., TRAUTMANN,
E., GAO, P., STEWART, T., ELIASMITH, C., BOAHEN, K. Silicon Neurons that Compute. International Conference on Artificial Neural Networks,
LNCS, Springer, Heidelberg. 2012, vol. 7552, p. 121–128 .
[57] CHUA, L. O. Memristor – The missing circuit element. IEEE Transaction
Circuit Theory. 1971, vol. 18, no. 5, p. 507–519.
[58] CHUA, L. O., KANG, S. M. Memristive devices and systems. Proceedings of
the IEEE. 1976, vol. 64, no. 2, p. 209–223.
[59] CHUA, L., KOMURO, M., MATSUMOTO, T. The double scroll family. IEEE
Transaction on CAS I: Fundamental Theory and Applications, 1986, vol. 33,
no. 11, ISSN 0098-4094.
[60] ITOH, M. Synthesis of electronic circuit for simulating nonlinear dynamics.
International Journal of Bifurcation and Chaos. 2001, vol.11, no.3, pp. 605653, ISSN 0218-1274.
[61] ITOH, M., CHUA, L. O. Memristor oscillators. International Journal of Bifurcation and Chaos. 2008, vol. 18, no. 11, p. 3183–3206.
[62] IU, H. H. C., YU, D. S., FITCH, A. L., SREERAM, V. Chaos control in a
memristor based circuit. In Proceedings of the IEEE International Symposium
on Circuits and Systems. 2011, p. 2946–2949.
[63] IZHIKEVICH, E.,M. Dynamical systems in neuroscience: the geometry of excitability and burstin. MIT Press, 2007, p. 457 pages. ISBN 978-0262090438.
[64] JAIKLA, W., LAHIRI, A. Resistor-less current–mode four–phase quadrature
oscillator using CCCDTA and grounded capacitors. AEU-International Journal of Electronics and Communications. 2012, vol. 66, no. 3, p. 214–218.
[65] JERABEK, J., SOTNER, R., VRBA, K. Tunable universal filter with current
follower and transconductance amplifiers and study of parasitic influences,
Journal of Electrical Engineering. 2011, vol. 62, no. 6, p. 317–326.
169
[66] KATSUTA, Y., KAWAKAMI, H. Bifurcations of equilibriums and periodic
solutions in nonlinear autonomous system with symmetry. IEICE Transaction
J75-A, 6, 1992, pp. 1035–1044.
[67] KENNEDY, M. P. Three steps to chaos — Part I: Evolution. IEEE
Transaction on Circuits and Systems I: Fundamental Theory and Applications.
1993, vol. 40, n. 10, p. 657-674, ISSN 1057-7122.
[68] KENNEDY, M. P. Three steps to chaos – Part II: A Chua’s circuit primer.
IEEE Transaction on Circuits and Systems I: Fundamental Theory and Applications. 1993, vol. 40, n. 10, p. 640-656. ISSN 1057-7122.
[69] KESKIN, A. U., AYDIN, C., HANCIOGLU, E., ACAR, C. Quadrature oscillator using current differencing buffered amplifiers (CDBA). Frequenz. 2006,
vol. 60, no. 3, p. 21–23.
[70] KESKIN, A. U., BIOLEK, D. Current mode quadrature oscillator using
current differencing transconductance amplifiers (CDTA). IEE Proceedings Circuits Devices and Systems. 2006, vol. 153, no. 3, p. 214–218.
[71] KLOEDEN, P. E. Synchronization of nonautonomous dynamical systems.
Electronic Journal of Differential Equations. 2003, p. 1–10, ISSN: 1072–6691.
[72] KLOEDEN, P. E., RASMUSSEN, M. Nonautonomous dynamical systems.
American Mathematical Society. 2011, 264 p.
[73] KOKSCH, N., SIEGMUND, S. Inertial manifolds for nonautonomous dynamical systems. Preprint/Technische Universirat Dresden. 2001, 24 p.
[74] KOLKA, Z., Synthesis of optimized piecewise–linear systems using similarity
transformation, Part I: Basic principles. Radioengineering. 2001, vol. 10, no.
3, pp. 5-7. ISSN 1210-2512.
[75] KUMNGERN, M., CHANWUTIUM, J., DEJHAN, K. Electronically tunable
multiphase sinusoidal oscillator using translinear current conveyors. Analog
Integrated Circuits and Signal Processing. 2010, vol. 65, no. 2, p. 327–334.
[76] KUMNGERN, M., JUNNAPIYA, S. A sinusoidal oscillator using translinear
current conveyors. Proceedings of the International Conference APPCAS.IEEE
Press, New York, 2010, p. 740–743
[77] KUNTMAN, H., OZPINAR, A. On the realization of DO-OTA-C oscillators.
Microelectronics Journal. 1998, vol. 29, no. 12, p. 991–997.
170
[78] LAHIRI, A. Current-mode variable frequency quadrature sinusoidal oscillator
using two CCs and four passive components including grounded capacitors.
Analog Integrated Circuits and Signal Processing. 2012, vol. 71, no. 2, p. 303–
311.
[79] LAHIRI, A. Explicit–current–output quadrature oscillator using second–
generation current conveyor transconductance amplifier. Radioengineering.
2009, vol. 18, no. 4, p. 522–526.
[80] LAHIRI, A. Novel voltage/current-mode quadrature oscillator using current
differencing transconductance amplifier. Analog Integrated Circuits and Signal
Processing. 2009, vol. 61, no. 2, p. 199–203.
[81] LAHIRI, A., GUPTA, M. Realizations of grounded negative capacitance using
CFOAs. Circuits, Systems and Signal Processing. 2011, vol. 30, no. 1, p. 134–
155.
[82] LEE, W. W., KUIPERS, B. J. Non intersection of trajectories in qualitative
phase space: a global constraint for qualitative simulation. In Proceedings of the
7𝑡ℎ National Conference on Artificial Intelligence, 1988, pp. 268–272.,ISBN 155860-095-7
[83] LEPIL, O. Deterministický chaos. Nové poznatky ve fyzice. Repronis, Ostrava,
2007, pp. 32-63. ISBN 978-80-7329-155-6.
[84] LINAREZ-BARRANCO, B., RODRIGUEZ-VAZQUEZ, A., SANCHEZSINENCIO, E., HUERTAS, L. CMOS OTA-C High frequency sinusoidal oscillators. IEEE Journal of Solid-state Circuits. 1991, vol. 26, no. 2, p. 160–165.
[85] LIU, S. I. Single-resistance-controlled/ voltage-controlled oscillator using
current conveyors and grounded capacitors. Electronics Letters. 1995, vol. 31,
no. 5, p. 337–338.
[86] LLOYD, J., RONDONI, L., MORRISS, G. P. Breakdown of ergodic behavior
in the Lorentz gas. Physical Review E , 1994, vol. 50, no. 5, pp. 3416–3421.
[87] LORENZ, E. N. Deterministic nonperiodic flow. Journal of the Atmospheric
Sciences, Jan. 1963, vol. 20, pp. 130–141.
[88] LU, J., CHEN, G. Generating multiscroll chaotic attractors: Theories, methods and applications. International Journal of Bifurcation and Chaos. 2006,
vol. 16, no. 4, pp. 775–858.
171
[89] LU, J., HAN, F., YU, X., CHEN, G. Generating 3-D multi-scroll chaotic attractors: A hysteresis series switching method. Automatica. 2004, pp. 1677–
1687.
[90] MACUR, J. Úvod do teorie dynamických systémů a jejich simulace. Brno:
PC-DIR, s.r.o., 1994, pp. 1-87. ISBN80-214-069.
[91] MAHESHWARI, S., CHATUVERDI, B. High output impedance CMQOs
using DVCCs and grounded components. International Journal of Circuit Theory and Applications. 2011, vol. 39, no. 4, p. 427–435.
[92] MANCHO, A. M., MENDOZA, C. The phase portrait of aperiodic non–
autonomous dynamical systems. ARXIV. 06/2011, 35 p.
[93] MARCELLIS, A., FERRI, G., GUERRINI, N. C., SCOTTI, G., STORNELLI,
V., TRIFILETTI, A. The VGC–CCII: a novel building block and its application to capacitance multiplication. Analog Integrated Circuits and Signal
Processing. 2009, vol. 58, no. 1, p. 55–59.
[94] MARTINEZ, P. A., MONGE-SANZ, B. M. Single resistance controlled oscillator using unity gain cells. Microelectronics Reliability. 2005, vol. 45, no. 1,
p. 191–194.
[95] MARTINEZ, P. A., SABADELL, J., ALDEA, C. Grounded resistor controlled
sinusoidal oscillator using CFOAs. Electronics Letters. 1997, vol. 33, no. 5,
p. 346–348.
[96] MARTINEZ-GARCIA, A., GRAU-SALDES, A., BOLEA-MONTE, Y.,
GAMIZ-CARO, J. On discussion on Barkhausen and Nyquist stability criteria. Analog Integrated Circuits and Signal Processing. 2012, vol. 70, no. 3,
p. 443–449.
[97] MIKSL, J. Analýza, vlastnosti a aplikace komerčně dostupných proudových
násobiček. Diplomová práce, Brno: VUT, FEKT, 2011, 79 p.
[98] MINAEI, S., CICEKOGLU, O. New current–mode integrator and all–pass
section without external passive elements and their application to design a
dual–mode quadrature oscillator. Frequenz. 2003, vol. 57, no. 1–2, p. 19–24.
[99] MINAEI, S., SAYIN, O. K., KUNTMAN, H. A new CMOS electronically
tunable current conveyor and its application to current–mode filters. IEEE
Transaction on Circuits and Systems I. 2006, vol. 53, no. 7, p. 1448–1457.
172
[100] MUTHUSWAMY, B. Implementing memristor based chaotic circuits. International Journal of Bifurcation and Chaos. 2010, vol. 20, no. 5, p. 1335–1350.
[101] MUTHUSWAMY, B., CHUA, L. O. Simplest chaotic circuit. International
Journal of Bifurcation and Chaos. 2010, vol. 20, no. 5, p. 1567–1580.
[102] MUTHUSWAMY, B., KOKATE, P. P. Memristor–based chaotic circuits.
IETE Technical Review. 2009, vol. 26, no. 6, p. 415–426.
[103] NAKAGAWA, S., SAITO, T. An RC OTA hysteresis chaos generator. IEEE
Transactions on Circuits and Systems I: Fundamental Theory and Applications. 1998, vol. 45, no. 2, p. 182–186.
[104] NAKAGAWA, S., SAITO, T. Design and control of RC VCCS 3-D hysteresis
chaos generators. IEEE Transactions on Circuits and Systems I: Fundamental
Theory and Applications. 1996, vol. 43, no. 12, p. 1019–1021.
[105] OPROCHA, P., WILCZYNSKI, P. Chaos in nonautonomous dynamical systems. Analele stiintifice ale Universitatii Ovidius Constanta. 2009, vol. 17,
no. 3, p. 209–221, ISSN 1844–0835.
[106] OZOGUS, S., ELWAKIL A. S., SALAMA, K. N. N-scroll chaos generator
using nonlinear transconductor. Elecron Lett, 2002, vol. 38 , pp. 685-–686.
[107] PALOUDA, H. National Semiconductors - current feedback amplifiers. Application note 597. 1989, p. 1–10.
[108] PANDEY, N., PAUL, S. K. Single CDTA–based current mode all–pass filter
and its applications. Journal of Electrical and Computer Engineering. 2011,
DOI: 10.1155/2011/897631, p. 1–5.
[109] PATIDAR V., SUD, K. Bifurcation and chaos in simple jerk dynamical systems. PRAMANA–journal of physics. Jan. 2005, vol. 64, no. 4, p. 75–93.
[110] PETERS, H. Non–autonomous complex dynamical systems. University of Michigan. 2005, 75 p.
[111] PETRAS, I. Fractional–Order Memristor–Based Chua’s Circuit. IEEE
Transactions on Circuits and Systems I: Regular Papers. 2011, vol. 58, no. 6,
p. 1323–1336.
[112] PETRZELA, J. Modelování zvláštních jevů ve vybraných nelineárních dynamických systémech. Disertační práce, Brno: VUT, FEKT, 2007, 160 p.
173
[113] PETRZELA, J. On the piecewise–linear approximation of the polynomial chaotic dynamics. In 34𝑡ℎ International Conference on Telecommunications and
Signal Processing. 2011, p. 319–323.
[114] PETRZELA, J., DRINOVSKY, J. High frequency chaos converters. In Proceedings - 2010 IEEE Region 8 International Conference on Computational Technologies in Electrical and Electronics Engineering, SIBIRCON-2010.
2010, p. 750–754.
[115] PETRZELA, J., GOTTHANS, T. Chaotic oscillators with single polynomial
nonlinearity and digital sampled dynamics. Przeglad Elektrotechniczny. 2011,
vol. 3, no. 1, p. 161–163.
[116] PETRZELA, J., KOLKA, Z., HANUS, S. Simple chaotic oscillator: from
mathematical model to practical experiment. Radioengineering. 2006, vol. 15,
no. 1, pp. 6-12. ISSN 1210-2512.
[117] PETRZELA, J., POSPISIL, V., HANUS, S. On the design of robust chaotic
oscillator. WSEAS Transactions on Circuits. 2005, vol. 5, no. 4, pp. 32-38.
ISSN 1109-2734.
[118] PETRZELA, J., PROKOPEC,J. Some practical experiments with simple driven dynamical systems. In Proceedings of the 19𝑡ℎ International Conference
RADIOELEKTRONIKA 2009, Bratislava 2009. p. 247–250. ISBN 978-1-42443537-1.
[119] PETRZELA, J., VYSKOCIL, P., PROKOPEC,J. Fundamental oscillators
based on diamond transistors. Proceedings of the 20𝑡ℎ International Conference RADIOELEKTRONIKA 2010, Brno 2010. p. 217–220.
[120] POGGI, T., SCIUTTO, A., STORACE, M. Piecewise linear implementation
of nonlinear dynamical systems: from theory to practice. Electronics Letters.
2009, vol. 45, no 19, p. 966 – 967. ISSN 0013-5194.
[121] POSCH, H. A., HOOVER, W. G., VESELY, F. J. Canonical dynamics of the
Nóse Oscillator: stability, order, and chaos. Physical Review A, 1986, vol. 33,
no. 6, pp. 4253–4265.
[122] POSPISIL, J., BRZOBOHATY, J., KOLKA, Z., HORSKA, J. New canonical
state models of Chua´s circuit family. Radioengineering. 1999, vol. 8, no. 3,
pp. 1-5. ISSN 1210-2512.
174
[123] POSPISIL, J., BRZOBOHATY, J., KOLKA, Z., HORSKA, J. Simplest ODE
equivalents of Chua´s equations. International. International Journal of Bifurcation and Chaos. 2000, vol. 10, no. 1, pp. 1-23.
[124] POSPISIL, J., KOLKA, Z., HORSKA, J., BRZOBOHATY, J. New reference
state model of the third–order piecewise–linear dynamical system. Radioengineering. 2000, vol. 9, no. 3, pp. 1-4. ISSN 1210-2512.
[125] POTZSCHE, C. Bifurcations in nonautonomous dynamical systems: results
and tools in discrete time. In Proceedings of the International Workshop Future
Directions in Difference Equations. June 13-17, 2011, Vigo, Spain, p. 163–212,
ISBN: 978–84–8158–541–4.
[126] POTZSCHE, C. Nonautonomous dynamical systems. Lecture Notes, WS
2010/11, TU München, Feb. 2011, 82 p.
[127] PSYCHALINOS, C., SPANIDOU, A. Current amplifier based grounded and
floating inductance simulators. AEU-International Journal of Electronics and
Communications. 2006, vol. 60, no. 2, p. 168–171.
[128] QI, A., WANG, G. Chaotic oscillator based on memristor and its circuit implementation. In Proceedings of the 4𝑡ℎ International Workshop on Chaos-Fractals
Theories and Applications. 2011, p. 328–331.
[129] RIAZ, A., ALI, M. Chaotic communications, their applications and advantages over traditional methods of communication. In Proceedings of the 6𝑡ℎ
International Symposium on Communication Systems, Networks and Digital
Signal Processing. 2008, p. 21–24.
[130] RODRIGUEZ-VAZQUEZ, A., LINAREZ-BARRANCO, B., HUERTAS, L.,
SANCHEZ-SINENCIO, E. On the design of voltage–controlled sinusoidal oscillators using OTA´s. IEEE Transaction on Circuits and Systems. 1990,
vol. 37, no. 2, p. 198–211.
[131] SALEM, S. B., FAKHFAKH, M., MASMOUDI, D. S., L., LOULOU, M.,
LOUMEAU, P., MASMOUDI, N. A high performance CMOS CCII and high
frequency applications. Analog Integrated Circuits and Signal Processing. 2006,
vol. 49, no. 1, p. 71–78.
[132] SANDRI, M., Numerical calculation of Lyapunov exponents. The Mathematica
Journal. 1196, vol. 6, no. 3, 1996, pp. 78–84.
175
[133] SANCHEZ–SINENCIO, E., RAMIREZ–ANGULO, J., LINARES–
BARRANCOM, B., RODRIGUEZ–VAZQUEZ, A. Operational transconductance amplifier-based nonlinear function syntheses. IEEE Journal of
Solid-State Circuits. Dec. 1989, vol. 24, no. 6, pp. 1576–1586.
[134] SCANLAN, S. O. Synthesis of piecewise–linear chaotic oscillators with prescribed eigenvalues. IEEE Transactions on CAS I. 1999, vol. 46, no. 9, pp.
1057-1064. ISSN 1057-7122.
[135] SEDIGHI, B., BAKHTIAR, M. S. Variable gain current mirror for high–speed
applications. IEICE Electronics Express. 2007, vol. 4, no. 8, p. 277–281.
[136] SENANI, R. Realization of a class of analog signal processing/signal generation circuits: novel configurations using current feedback opamps. Frequenz.
1998, vol. 52, no. 9–10, p. 196–206.
[137] SENANI, R., GUPTA, S. S. Synthesis of single–resistancecontrolled oscillators
using CFOAs: simple state–variable approach. IEEE Proceedings on Circuits,
Devices and Systems. 1997, vol. 144, no. 2, p. 104–106.
[138] SHARAD, M., AUGUSTINE, C., PANAGOPOULOS, G., ROY, K. Proposal For Neuromorphic Hardware Using Spin Devices. eprint arXiv:1206.3227.
06/2012.
[139] SHI-XIANG, S., GUO-PING, Y., HUA, C. A new CMOS electronically tunable current conveyor based on translinear circuits. In Proceedings of the 7𝑡ℎ
International Conference ASICON 2007. IEEE Press, New York. 2007. p. 569–
572.
[140] SINGH, V. Discussion on Barhausen and Nyquist stability criteria. Analog
Integrated Circuits and Signal Processing. 2010, vol. 62, no. 3, p. 327–332.
[141] SINGH, V. Equivalent forms of dual-OTA RC oscillators with application to
grounded–capacitor oscillators. IEE Proceedings - Circuits Devices Systems.
2006, vol. 153, no. 2, p. 95–99.
[142] SIRIPRUCHYANUN, M., CHANAPROMMA, C., SILAPAN, P., JAIKLA,
W. BiCMOS current–controlled current feedback amplifier (CC-CFA) and its
applications. WSEAS Transactions on Electronics. 2008, vol. 6, no. 5, p. 203–
219.
[143] SMALL, M. Applied nonlinear time series analysis: applications in physics,
physiology and finance. World Scientific Publishing Company. 2005.
176
[144] SMITH, K. C., SEDRA, A. A second generation current conveyor and its
applications. IEEE Transaction on Circuit Theory CT. 1970, vol. 17, no. 2,
p. 132–134.
[145] SMITH, K. C., SEDRA, A. The current Conveyor: a new circuit building
block. IEEE Proceeding CAS. 1968, vol. 56, no. 3, p. 1368–1369.
[146] SMITH, L. S., SMALE, S. Handbook of nature–inspired and innovative computing: integrating classical models with emerging technologies. Springer, New
York, 2006, pp. 433–475, ISBN 978-0-387-27705-9.
[147] SOLIMAN, A. M. CMOS balanced output transconductor and applications
for analog VLSI. Microelectronics Journal. 1999, vol. 30, no. 1, p. 29–39.
[148] SOLIMAN, A. M. Novel oscillators using current and voltage followers. Journal
of the Franklin Institute. 1998, vol. 335, no. 6, p. 997–1007.
[149] SOLIMAN, A. M. Synthesis of grounded capacitor and grounded resistor oscillators. Journal of the Franklin Institute. 1999, vol. 336, no. 4, p. 735–746.
[150] SOTNER, R., HERENCSAR, N., JERABEK, J., KOTON, J., DOSTAL, T.,
VRBA, K. Quadrature oscillator based on modified double current controlled
current feedback amplifier. Proceedings of the 22𝑛𝑑 International Conference
Radioelektronika 2012. IEEE Press, New York. 2012. p. 275–278.
[151] SOTNER, R., JERABEK, J., DOSTAL, T., VRBA, K. Multifunctional adjustable current mode biquads based on distributed feedback voltage mode
prototype with OTAs. International Journal of Electronics. Jul. 2010, vol. 97,
no. 7, p. 797–809.
[152] SOTNER, R., JERABEK, J., HERENCSAR, N., DOSTAL, T., VRBA, K.
Electronically adjustable modification of CFA: double current controlled CFA
(DCC-CFA). Proceedings of the 35𝑡ℎ International Conference on Telecommunications and Signal Processing (TSP 2012). IEEE Press, New York. 2012.
p. 401–405.
[153] SOTNER, R., JERABEK, J., PETRZELA, J., DOSTAL, T., VRBA, K.
Electronically tunable simple oscillator based on single–output and multiple output transconductor. IEICE Electronics Express. 2009, vol. 6, no. 20,
p. 1476–1482.
[154] SOTNER, R., JERABEK, J., PROKOP, R., VRBA, K. Current gain controlled CCTA and its application in quadrature oscillator and direct frequency
modulator. Radioengineering. 2011, vol. 21, no. 1, p. 317–326.
177
[155] SOTNER, R., SLEZAK J., DOSTAL T. Influence of mirroring of current output responses through grounded passive elements. In Proceedings of the 20𝑡ℎ
International Conference Radioelektronika, 2010, p. 1–4.
[156] SOULIOTIS, C., PSYCHALINOS, C. Electronically controlled multiphase sinusoidal oscillators using current amplifiers. International Journal of Circuit
Theory and Applications. 2009, vol. 37, no. 1, p. 43–52.
[157] SOULIOTIS, C., PSYCHALINOS, C. Harmonic oscillators realized using
current amplifiers and grounded capacitors. International Journal of Circuit
Theory and Applications. 2007, vol. 35, no. 2, p. 165–173.
[158] SPANY, V., GALAJDA, P., GUZAN, M., PIVKA, L., OLEJAR, M. Chua’s
singularities: great moracle in circuit theory. International Journal of Bifurcation and Chaos, 2010, pp. 2993–3006.
[159] SPROTT, J., C. Chaos and time–series analysis. Oxford University Press,
2003, 507 pages, ISBN 01-985-0840-9.
[160] SPROTT, J., C. Some simple chaotic flows. Physical Review E., 1994, vol. 50,
no. 2, pp. 647–650.
[161] SPROTT, J., C. ELEGANT CHAOS: Algebraically simple chaotic flows.
World Scientific: Singapore, 2010, 281 p., ISBN–13 978–981–283–881–0.
[162] SPROTT, J. C., LINZ, S. J. Algebraically simple chaotic flow. International
Journal of Chaos Theory and Applications, 2000, vol. 5, no. 2, pp. 1–20.
[163] STORACE, M., LINARO, D., LANGE, E. The Hindmarsh-Rose neuron model: bifurcation analysis and piecewise linear approximations. Chaos. 2008, vol.
18, no. 3, pp. 1-10. ISSN 1089-7682.
[164] STRUKOV, D. B., SNIDER, G. S., STEWART, G. R., WILLIAMS, R. S.
The missing memristor found. Nature. 2008, vol. 453, p. 80–83.
[165] SURAKAMPONTIRN, W., KUMWACHARA, K. CMOS-based electronically
tunable current conveyor. Electronics Letters. 1992, vol. 28, no. 14, p. 1316–
1317.
[166] SURAKAMPONTIRN, W., THITIMAJSHIMA, W. Integrable electronically
tunable current conveyors. IEE Proceedings-G. 1988, vol. 135, no. 2, p. 71–77.
[167] SVOBODA, J. A., MCGORY, L., WEBB, S. Applications of commercially
available current conveyor. International Journal of Electronics. 1991, vol. 70,
no. 1, p. 159–164.
178
[168] TANGSRITA, W. Electronically tunable multi-terminal floating nullor and its
application. Radioengineering. 2008, vol. 17, no. 4, p. 3–7.
[169] TANGSRITA, W., PUKKALANUN, T. Digitally programmable current
follower and its applications. AEU-International Journal of Electronics and
Communications. 2009, vol. 63, no. 5, p. 416–422.
[170] TAO, Y., FIDLER, J. K. Electronically tunable dual–OTA second–order sinusoidal oscillators/filters with non–interacting controls: a systematic synthesis
approach. IEEE Transaction on Circuits and Systems I. 2000, vol. 47, no. 2,
p. 117–129.
[171] THOMPSON, J. M. T., STEWART, H. B. Nonlinear dynamics and chaos. 2
edition, Wiley, 2002, 460 p. ISBN 04-718-7684-4.
[172] TREJO–GUERRA, R., TLELO–CUAUTLE, E., SANCHEZ–LOPEZ,
C.,MUNOZ–PACHECO J.M., CRUZ–HERNANDEZ, C., Realization of multiscroll chaotic attractors by using current–feedback operational amplifers.
Revista Mexicana de Fisica, 497–504, 2010, vol. 56, pp. 268–274.
[173] VALSA, J., BIOLEK, D., BIOLEK, Z. An Analogue Model of the Memristor.
International Journal of Numerical Modeling: Electronic Networks, Device and
Fields. 2011, vol. 24, p. 400–408.
[174] WAGEMAKERS, A. Electronic modelling of complex dynamics. Disertation
thesis, Madrid: Universidad Rey Juan Carlos, Departamento de Fisica, 2008,
137 p.
[175] WANG, W., WANG, W., TAN, D. A New Memristor Based Chaotic Circuit.
Fourth International Workshop on Chaos-Fractals Theories and Applications.
2011, p. 57–60.
[176] WANG, Z. 2-MOSFET transresistor with extremely low distortion for output
reaching supply voltage. Electronics Letters. 1990, vol. 26, no. 13, p. 951–952.
[177] WANGENHEIM, L. On the Barkhausen and Nyquist stability criteria. Analog
Integrated Circuits and Signal Processing. 2011, vol. 66, no. 1, p. 139–141.
[178] WEIHENG, S., CHUNFU, L., JUEBANG, Y. A Memristor Based Chaotic
Oscillator. In Proceedings of the International Conference on Communications,
Circuits and Systems. 2009, p. 955–957.
[179] WIGGINS, S. Introduction to applied nonlinear dynamical systems and chaos.
Springer; 2𝑛𝑑 edition, 2003, 808 p., ISBN: 978–03–8700–177–7.
179
[180] YENER, S. KUNTMAN, H. A New CMOS Based Memristor Implementation.
In Proceedings of the International Conference on Applied Electronics. 2012,
p. 345–348.
[181] YESIL, A., KACAR, F., KUNTMAN, H. New simple CMOS realization of
voltage differencing transconductance amplifier and its RF filter application.
Radioengineering. 2011, vol. 20, no. 3, p. 632–637.
[182] YONG, Ch., XIA, L., Qi, H., CHANGHUA, Z. Chaos system filter on statespace model and EKF. In Proceedings of the IEEE International Conference on
Automation and Logistics, Shenyang, China, 5-7 August, 2009. Northeastern
University, Shenyang, China, 2009, p. 1259 - 1263. ISBN 978-1-4244-4794-7.
[183] YU, S. F., SHUM, P., NGO, N. Q. Performance of optical chaotic communication systems using multimode vertical cavity surface emitting lasers. Optics
Communications. 2001, vol. 200, no. 1-6, pp. 143-152.
[184] YU, Q., QIN, Z., YU, J., MAO Y. Realization of an analog model of memristor based on light dependent resistor. In Proceedings of the International
Conference on Communications, Circuits and Systems. 2009, p. 974–977.
[185] YUCE, E., MINAEI, S., ALPASLAN, H. Novel CMOS Technology-based Linear Grounded Voltage Controlled Resistor. Journal of Circuits, Systems and
Computers. 2011, vol. 20, no. 3, p. 447–455.
[186] ZHANG, J., ZHANG, H., ZHANG, G. Controlling chaos in a memristor–based
Chua’s circuit. In Proceedings of the International Conference on Communications, Circuits and Systems. 2009, p. 961–963.
[187] ZHAO, J., YONG-BIN, K. Circuit implementation of FitzHugh-Nagumo neuron model using field programmable analog arrays. In Proceedings of the 50𝑡ℎ
Midwest Symposium on Circuits and Systems. Montreal, 5-8 August, 2007.
Institute of Electrical and Electronics Engineers (IEEE), 2007, pp. 772 - 775.
ISSN 1548-3746.
[188] Low Cost Analog Multiplier AD633 [Online]. Analog Devices, 04/2011, 12 p.,
Available at: http://www.analog.com.
[189] Precision BiFET Quad Op Amp AD713 [Online]. Analog Devices, 2011, 20
p., Available at: http://www.analog.com.
[190] AD8138: Low Distortion Differential ADC Driver [Online]. Analog Devices,
01/2006, 24 p., Available at: http://www.analog.com.
180
[191] Monolithic Op Amp AD844 [Online]. Analog Devices, 02/2009, 20 p. Available
at: http://www.analog.com.
[192] BUF634: 250 mA High-Speed Buffer [Online]. Texas Instruments, 09/2000, 20
p., Available at: http://www.ti.com.
[193] EL2082: Current-Mode Multiplier [Online]. Intersil (Elantec), 01/1996, 14 p.,
Available at: http://www.intersil.com.
[194] EL4083: Current-Mode Four-Quadrant Multiplier [Online]. Intersil (Elantec),
1995, 14 p., Available at: http://www.intersil.com.
[195] LT1364: Dual and Quad 70 MHz, 1000 V/𝜇s, Op Amps [Online]. Linear Technology, 1994, 12 p., Available at: http://www.linear.com.
[196] Wideband Transconductance Amplifier MAX435 [Online]. Maxim, 9/2011,
17p. Available at: http://www.maxim-ic.com.
[197] Wide Bandwidth Operational Transconductance Amplifier and Buffer OPA 860
[Online]. Texas Instruments, 08/2008, 33 p. Available at: http://www.ti.com.
[198] JFET-Input Operational Amplifier TL084 [Online]. Texas Instruments, 2004,
41 p. Available at: http://www.ti.com.
[199] VCA810: High Gain Adjust Range, Wideband, variable gain amplifier [Online].
Texas Instruments, 12/2010, 30 p., Available at: http://www.ti.com.
OWN PUBLICATIONS:
[200] HRUBOS, Z., GOTTHANS, T., PETRZELA, J. Circuit realization of the
inertia neuron. In Proceedings of the 21𝑠𝑡 International Conference RADIOELEKTRONIKA 2011. Brno, Tribun EU s.r.o. Gorkeho 41, 602 00 Brno. 2011,
p. 215–218. ISBN 978-1-61284-322-3.
[201] HRUBOS, Z., PETRZELA, J. Univerzální oscilátor pro modelování dynamických systémů. Elektrorevue - Internetový časopis (http://www.elektrorevue.cz).
2010, vol. 8, no. 3, p. 1–5. ISSN 1213-1539.
[202] HRUBOS, Z., PETRZELA, J. Implementations of a chaotic system based on
state equations. In Proceedings of the 8𝑡ℎ International Conference Králíky
2010. 2010, p. 56–59. ISBN 978-80-214-4139-2.
181
[203] HRUBOS, Z., PETRZELA, J. Modeling and analysis of a chaotic system based
on state equations in voltage mode. In New Information and Multimedia Technologies - NIMT 2010. Brno, VUT Brno. 2010, p. 12–15. ISBN 978-80-2144126-2.
[204] HRUBOS, Z., SOTNER, R. Practical tests of current follower based on discrete commercially available transistors. In Proceedings of the 16𝑡ℎ Conference
Student EEICT 2010 Volume 4, 2010. Brno, NOVPRESS s.r.o. nám. Republiky 15, 614 00 Brno. 2010, p. 17–21. ISBN 978-80-214-4079-1.
[205] HRUBOS, Z. Universal voltage–mode third–order oscillator. In Proceedings of
the 15𝑡ℎ Student Competition EEICT . Brno, FEKT VUT Brno. 2009, vol. 2,
p. 134–136. ISBN 978-80-214-3870-5.
[206] HRUBOS, Z. Chaotický oscilátor založený na integrátorové syntéze. In Proceedings of the 13𝑡ℎ Student Competition EEICT. Brno, FEKT VUT Brno.
2007, p. 1–3.
[207] HRUBOS, Z., GOTTHANS, T., PETRZELA, J. Two equivalent circuit realizations of the Ueda’s oscillator. In Proceedings of 18𝑡ℎ International Conference
Mixdes 2011, Gliwice, Polsko. 2011, p. 694–698. ISBN 978-83-932075-0-3.
[208] HRUBOS, Z., GOTTHANS, T. Analysis and synthesis of chaotic circuits using
memristor properties. Journal of Electrical Engineering. 2014, vol. 65, no. 3,
p. 129–136. ISSN1̃335-3632. (IF=0,37).
[209] HRUBOS, Z. Novel circuit implementation of universal and fully analog chaotic oscillator. Przeglad Elektrotechniczny. 2012, vol. 07a, p. 18–22. ISSN0̃0332097. (IF=0,244).
[210] HRUBOS, Z., PETRZELA, J. On the possibility of chaos destruction via parasitic properties of the used active devices. In Proceedings of the 3𝑟𝑑 International conference on Circuits, Systems, Control, Signals (CSCS’12). Barcelona,
Spain. 2012, p. 204–208. ISBN 978-1-61804-131-9.
[211] HRUBOS, Z., GOTTHANS, T. Analysis and synthesis of the chaotic circuits
based on OTA Elements. In Proceedings of the 18𝑡ℎ Iinternational Conference
on Applied Electronics . Plzeň. 2012, p. 103–106. ISBN 978-80-261-0038-6.
[212] HRUBOS, Z., GOTTHANS, T., SOTNER, R. Influence of gain changes for
tuning purposes on observance of oscillation condition in simple oscillator.
In Proceedings of the 10𝑡ℎ International Conference Vsacký Cáb 2012. 2012,
p. 1–4. ISBN 978-80-214-4579-6.
182
[213] HRUBOS, Z. Synthesis of memristor – based chaotic circuit. In Proceedings of
the 35𝑡ℎ International Conference on Telecommunications and Signal Processing TSP 2012, 3.-4. 7.2012, Prague, Czech Republic. 2012, p. 416–420. ISBN
978-1-4673-1116-8.
[214] HRUBOS, Z., GOTTHANS, T., PETRZELA, J. Electronic experiments with
dynamical model of thermostat system. Elektrorevue - Internetový Casopis
(http://www.elektrorevue.cz). 2012, p. 64–70. ISSN1̃213-1539.
[215] HRUBOS, Z. Analogové oscilátory generující nekonvenční spojité signály. In
Pokročilé metody, struktury a komponenty elektronické bezdrátové komunikace.
Brno, Ing. Vladislav Pokorný - LITERA BRNO, TAbor 2813/43A. Brno,
61200. . 2011, p. 22–25. ISBN 978-80-214-4368-6.
[216] HRUBOS, Z., PETRZELA, J. Modeling of nonstandard systems with quadratic vector field in comparison with circuitry realization. In Recent Researches
in Mathematical Methods in Electrical Engineering and Computer Science.
Francie. 2011, p. 104–109. ISBN 978-1-61804-051-0.
[217] HRUBOS, Z., KINCL, Z., PETRZELA, J. Analytical analysis and synthesis of
the switched-capacitor filters supported by Program FilterCAD. In Proceedings
of the 9𝑡ℎ International conference Vsacký CAb 2011. 2011, p. 45–48. ISBN
978-80-214-4319-8.
[218] HRUBOS, Z., PETRZELA, J., GOTTHANS, T. Novel circuit implementation
of the Nóse-Hoover thermostated dynamic system. In Proceedings of the 34𝑡ℎ
International Conference on Telecommunications and Signal Processing TSP
2011, 18-20.8.2011, Budapest, Hungary. 2011, p. 307–311. ISBN 978-1-45771409-2.
[219] GOTTHANS, T., HRUBOS, Z. Multi grid chaotic attractors with discrete
jumps. Journal of Electrical Engineering. 2013, vol. 64, p. 118–122. ISSN1̃3353632. (IF=0,37).
[220] RAIDA, Z., KOLKA, Z., MARSALEK, R., PETRZELA, J., PROKES, A.,
SEBESTA, J., GOTTHANS, T., HRUBOS, Z., KINCL, Z., KLOZAR, L.,
POVALAC, A., SOTNER, R., KADLEC, P. Communication subsystems for
emerging wireless technologies. Radioengineering. 2012, vol. 21, no. 4, p. 1–14.
ISSN1̃210-2512. (IF=0,687).
[221] SOTNER, R., HRUBOS, Z., SLEZAK, J., DOSTAL, T. Simply adjustable
sinusoidal oscillator based on negative three–port current conveyors. Radioengineering. 2010, vol. 19, no. 3, p. 446–453. ISSN 1210-2512. (IF=0,687).
183
[222] SOTNER, R., JERABEK, J., HERENCSAR, N., HRUBOS, Z., DOSTAL, T.,
VRBA, K. Study of adjustable gains for control of oscillation frequency and
oscillation condition in 3R-2C oscillator. Radioengineering. 2012, vol. 21, no. 1,
p. 392–4022. (IF=0,687).
[223] SOTNER, R., HRUBOS, Z., SEVCIK, B., SLEZAK, J., PETRZELA, J., DOSTAL, T. An example of easy synthesis of active filter and oscillator using
signal flow graph modification and controllable current conveyors. Journal of
Electrical Engineering. 2011, vol. 62, no. 5, p. 258–266. (IF=0,37).
[224] SOTNER, R., HRUBOS, Z., HERENCSAR, N., JERABEK, J., DOSTAL, T.,
VRBA, K. Precise electronically adjustable oscillator suitable for quadrature
signal generation employing active elements with current and voltage gain
control. Circuits systems and signal processing. 2014, vol. 33, no. 1, p. 1–35.
ISSN 0278-081X. (IF=1,118).
[225] PETRZELA, J., HRUBOS, Z. A note on chaos conversion in frequency domain. In Recent Advances in Applied Mathematics, WSEAS Transactions on
Systems. Kanárské ostrovy, WSEAS. 2009, p. 19–22. ISBN 978-960-474-138-0.
[226] PETRZELA, J., HRUBOS, Z. Simplest chaos converters: modeling, analysis
and future perspectives. In Recent Advances in System Science and Simulation,
WSEAS Transactions on Systems. Itálie, WSEAS. 2009, p. 160–163. ISBN
978-960-474-131-1.
[227] PETRZELA, J., HRUBOS, Z., GOTTHANS, T. Canonization of dynamical
system reprezentation using trivial linear transformations. In Proceedings of
the 22𝑛𝑑 International Conference Radioelektronika 2012. Brno, UREL FEKT
VUT. 2012, p. 1–4. ISBN 978-80-214-4468-3.
[228] PETRZELA, J., GOTTHANS, T., HRUBOS, Z. General review of the passive networks with fractional–order dynamics. In Proceedings of International
Conference on Circuits, Systems, Control, Signals 2012. Barcelona, WSEAS,
NAUN. 2012, p. 172–177. ISBN 978-1-61804-131-9.
[229] PETRZELA, J., GOTTHANS, T., HRUBOS, Z. Modeling deterministic chaos
using electronic circuits. In Radioengineering. 2011, vol. 20, no. 2, p. 438–
444.(IF=0,687).
[230] PETRZELA, J., GOTTHANS, T., HRUBOS, Z. Behavior identification in
the real electronic circuits. In Proceedings of the 18𝑡ℎ International Conference
Mixdes 2011. Lodz, Polsko. 2011, p. 438–441. ISBN 978-83-928756-3-5.
184
[231] PETRZELA, J., GOTTHANS, T., HRUBOS, Z. Analog implementation of
Gotthans-Petrzela oscillator with virtual equilibria. In Proceedings of the 21𝑠𝑡
International Conference Radioelektronika 2011. Brno. 2011, p. 53–56. ISBN
978-1-61284-322-3.
[232] GOTTHANS, T., PETRZELA, J., HRUBOS, Z., BAUDOIN, G. Parallel particle swarm optimization on chaotic solutions of dynamical systems. In Proceedings of the 22𝑛𝑑 International Conference Radioelektronika 2012. Brno,
UREL FEKT VUT. 2012, p. 1–4. ISBN 978-80-214-4468-3.
[233] GOTTHANS, T., PETRZELA, J., HRUBOS, Z. Analysis of Hindmarsh-Rose
neuron model and novel circuitry realisation. In Proceedings of the 18𝑡ℎ International Conference Mixdes 2011. Lodz, Polsko. 2011, p. 576– 579. ISBN
978-83-928756-3-5.
[234] GOTTHANS, T., PETRZELA, J., HRUBOS, Z. Analogue circuitry realization
of neuron network. In CHAOS 2011. Book of Abstracts 4𝑡ℎ Chaotic Modeling
and Simulation International Conference. Agios Nikolaos. 2011, p. 45–52.
[235] GOTTHANS, T., PETRZELA, J., HRUBOS, Z. Advanced parallel processing
of Lyapunov exponents verified by practical circuit. In Proceedings of the 21𝑠𝑡
International Conference Radioelektronika 2011. Brno. 2011, p. 405–408. ISBN
978-1-61284-322-3.
[236] KINCL, Z., HRUBOS, Z., PETRZELA, J., KOLKA, Z. Acquisition unit for
real filter parameters measurements. In Proceedings of 9𝑡ℎ International Conference Vsacký CAb 2011. 2011, p. 65–68. ISBN 978-80-214-4319-8.
[237] KINCL, Z., SOTNER, R., HRUBOS, Z. Application of current–mode multipliers in adjustable oscillator. In Proceedings of the 17𝑡ℎ Conference EEICT.
Brno, Czech Republic, NOVPRESS. 2011, p. 46– 50. ISBN 978-80-214-4273-3.
185
CURRICULUM VITAE
MSc. Zdenek HRUBOS
Date of Birth:
Place of Birth:
Country of citizenship:
Marital status:
Disabled with special needs:
6-11-1984
Uherské Hradiště
Czech Republic
Single
None
Contact info:
Telephone:
E-mail:
Contact address:
+420776135198
[email protected]
Hustenovice 107, 68703, Czech Republic
Work experience:
02/2013 – present
VVÚ Brno s.p. (Military Research Institute, State Enterprise)
Profession: RF Design Engineer, PCB Designer Engineer
Country: Czech Republic
01/2012 - 12/2012
FEEC BUT Brno
Innovation of computer exercises in the subject Analog Electronic Circuits.
Investigator in innovation of computer exercises in the subject Analog
Electronic Circuits (FRVŠ no. 2442/2012/G1).
Profession: Electrical engineer
Country: Czech Republic
09/2011 - 12/2011
FEEC BUT Brno
Advanced Methods, Structures and Components of Electronic Wireless
Communication.
Doctoral project of Grant Agency Czech Republic no. 102/08/H027.
Profession: Electrical engineer
Country: Czech Republic
01/2011 - 12/2011
FEEC BUT Brno
Proposal of modern computer tasks in the subject Analog Filter Design.
Co-investigator in proposal of modern computer tasks in the subject Analog
filter design (FRVS no. 1442/2011/G1).
Profession: Electrical engineer
Country: Czech Republic
Education:
2009 – present
2007 - 2009
2004 - 2007
Doctor of Philosophy (PhD), FEEC BUT Brno
Electrical engineering, telecommunications and computer technologies
Postgraduate studies at the Department of Radio Electronics,
Study Programme: Electrical, Electronic, Communication and Control
Technology
Topic of dissertation thesis: Unconventional signals generators
Master’s degree (MSc) – inženýr (Ing.), FEEC BUT Brno
Electrical engineering, telecommunications and computer technologies
Department of Radio Electronics,
Study Programme: Electrical, Electronic, Communication and Control
Technology
Topic of master's thesis: Laboratory device with analog computational unit
AD538
Bachelor’s degree (BSc) – bakalář (Bc.), FEEC BUT Brno
Electrical engineering, telecommunications and computer technologies
Department of Radio Electronics,
CURRICULUM VITAE
Study Programme: Electrical, Electronic, Communication and Control
Technology
Topic of bachelor's thesis: Universal and fully analog oscillator
6 - 8 June 2012
Participation in Training School on Energy-aware RF Circuits and Systems
Design (Villa Griffone, University of Bologna Pontecchio Marconi, Bologna,
Italy)
26 - 28 January 2012
Participation in Training School on Technology Challenges for the Internet of
Things (University of Aveiro, Aveiro, Portugal)
20-22 June 2011
Participation in Training School on RF/Microwave System Design for Sensor
and Localization Applications (CTTC Castelldefels, Barcelona, Spain)
Certificates/Licenses:
50/78Sb. Certificate
Knowledge and skills:
Czech
English
IT knowledge:
Driving license:
Proficient / native speaker
Intermediate (B1)
Knowledge of Microsoft office programs (Word, Excel ...), knowledge of
electrical engineering programs (Altium Designer, Eagle, PSpice, Matlab,
Mathcad, ...)
B
Interests:
I'm interest in literature and sports (active and passive). Actively football,
hockey, cycling and skiing.
Selected publications in scientific journals:
HRUBOS, Z., GOTTHANS, T. Analysis and Synthesis of Chaotic Circuits Using Memristor Properties. Journal of
Electrical Engineering, 2014, 65(3), p. 129-136. ISSN: 1335- 3632. (IF=0,37).
HRUBOS, Z. Novel circuit implementation of universal and fully analog chaotic oscillator. Przeglad
Elektrotechniczny. 2012, vol. 07a, p. 18–22. ISSN:0033-2097. (IF=0,244).
GOTTHANS, T., HRUBOS, Z. Multi Grid Chaotic Attractors with Discrete Jumps. Journal of Electrical Engineering.
2013, vol. 64, p. 118–122. ISSN:1335-3632. (IF=0,37).
PETRZELA, J., GOTTHANS, T., HRUBOS, Z. Modeling deterministic chaos using electronic circuits.
Radioengineering. 2011. 20(2), p. 438 - 444. ISSN 1210-2512. (IF=0,687).
SOTNER, R., HRUBOS, Z., HERENCSAR, N., JERABEK, J., DOSTAL, T., VRBA, K. Precise electronically adjustable
oscillator suitable for quadrature signal generation employing active elements with current and voltage gain
control. Circuits systems and signal processing. 2014, vol. 33, no. 1, p. 1–35. ISSN:0278-081X. (IF=1,118).
Selected publications in international conferences:
HRUBOS, Z., PETRZELA, J. Modeling of Nonstandard Systems with Quadratic Vector Field in Comparison with
Circuitry Realization. In Recent Researches in Mathematical Methods in Electrical Engineering & Computer
Science. Francie. 2011. p. 104 - 109. ISBN 978-1-61804-051-0.
HRUBOS, Z., PETRZELA, J., GOTTHANS, T. Novel circuit implementation of the Nóse-Hoover thermostated
dynamic system. In Proceedings of the 34th International Conference on Telecommunications and Signal
Processing TSP 2011, 18‐20.8.2011, Budapest, Hungary. 2011. p. 307 - 311. ISBN 978-1-4577-1409-2.
HRUBOS, Z., GOTTHANS, T., PETRZELA, J. Two Equivalent Circuit Realizations of the Ueda's Oscillator. In
Proceedings of 18th International Conference Mixdes 2011. Gliwice, Polsko. 2011. p. 694 - 698. ISBN
978-83-932075-0-3.