Download Chapter 5: Forces in Equilibrium

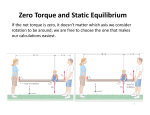
Forces
Unit 2: Forces
Chapter 5: Forces in Equilibrium
 5.1
The Force Vector
 5.2
Forces and Equilibrium
 5.3
Friction
 5.4
Torque and Rotational Equilibrium
5.1 Investigation: Working with Force Vectors
Key Question:
How can we use force vectors to
predict the acceleration of the car?
Objectives:

Resolve a vector into its x- and y-components.
Use the components of a vector to make predictions about
the motion of the Energy Car as it moves along the track.
 Apply Newton’ second law to distinguish between predicted
and measured values of net force.

Scalar quantities
 A scalar
is a quantity that can be
completely described by a single
value called its magnitude.
 Magnitude
means the amount,
and always includes units of
measurement.
 Temperature
is a good example
of a scalar quantity.
Vector quantities
 Sometimes
a single number does
not include enough information to
describe a measurement.
 A vector
is a quantity that
includes both magnitude and
direction.
 Vectors
are useful when giving
directions.
The force vector
 There
are three ways to describe force vectors.
 You
can represent a force vector with a graph, a
magnitude-angle pair, or an x-y pair.
 A force
forces.
vector has units of newtons, just like all
The force vector

The force vector is drawn as an arrow.

The length of the arrow shows the
magnitude of the vector, and the arrow
points in the direction of the vector.

When drawing a vector, you must choose
a scale.

A vector showing a force magnitude of 10
N, and the scale is 1 cm = 1 N, would
have an arrow 10 cm long.
The force vector

A force at an angle has the same effect
as two smaller forces aligned with the xand y-directions.

The horizontal 8.7-N and vertical 5-N
force applied together have the same
effect as one 10-N force applied at a 30°
angle.

Every force vector can be replaced by
perpendicular vectors called
components.

We can think of components as “adding
up” to equal the original force.
Polar coordinates
 One
way of writing a vector is
called polar coordinates.
— The first number (10 N) is
the magnitude, or strength
of the force.
— The second number is the
angle measured
counterclockwise from the
x-axis.
— This force is written (8.7, 5)
N.
Cartesian coordinates
 Mathematically,
when we
write a vector as (x, y) we are
using Cartesian coordinates.
 Cartesian
coordinates use
perpendicular x- and y-axes
like on graph paper.
Use of the Pythagorean theorem
 You
can check your components
by drawing a triangle.
 The
x and y-components are the
lengths of the triangle’s side and
the original vector is the
hypotenuse of a right triangle.
 The
Pythagorean theorem can be
used to find the lengths of any
side of a right triangle.
Pythagorean Theory
side b
side a
a 2 + b 2 = c2
hypotenuse, side c
Free-body diagrams
 A free-body
diagram is a diagram that uses vectors
to show all of the external forces acting on an object.
 A free-body
diagram of a book shows only the forces
acting on the book.
Free body diagrams
 A free-body
diagram for a monkey hanging from two
ropes includes all forces acting on the monkey.
 The
tension forces of the ropes (F1 and F2) acts on
the monkey, as well as gravity (Fw).
Finding force components
A man pulls a wagon with a force of 80 N at an
angle of 30 degrees. Find the x (horizontal) and y
(vertical) components of the force.
1. Looking for: … the x- and ycomponents of the force.
2.
Given: … the magnitude and direction
of the force.
3.
Relationships: The x- and ycomponents can found by graphing the
force to scale.
4.
Solution: x component is 70 N, y
component is 40 N
The net force
 The
free-body diagram will
help you see all of the forces
acting so you can find the
net force.
 The
net force is the the total
of all forces acting on an
object.
 If
the net force is zero, the
object is not moving.
The net force
 Consider
the forces acting
between books weighing
30 N on a 200 newton
table.
 A free-body
diagram can
help explain
mathematically how the
forces are acting on the
surfaces in contact.
Forces to consider in diagrams
Unit 2: Forces
Chapter 5: Forces in Equilibrium
 5.1
The Force Vector
 5.2
Forces and Equilibrium
 5.3
Friction
 5.4
Torque and Rotational Equilibrium
5.2 Investigation: Equilibrium Forces and
Hooke’s Law
Key Question:
How do you predict the force on a
spring?
Objectives:

Conduct experiments to determine the spring constants for
an extension spring and a compression spring.

Create and test a graphical model for spring data between
predicted and measured values of net force.
Forces and equilibrium
 When
the net force on an object is zero, we say the
object is in equilibrium.
 Newton’s
first law says an object’s motion does not
change unless a net force acts on it.
 If
the net force is zero, an object at rest will stay at
rest and an object in motion will stay in motion with
constant speed and direction.
Forces and equilibrium

Remember the book sitting on the
table?

The book exerts a contact force on
the table.

A contact force is a force between
the objects in contact, or between an
object and a surface.

The table exerts an upward force on
the book called the normal force.

In mathematics, normal means
perpendicular.
Equilibrium
 Newton’s
third law
explains why normal
forces exist.
 The
third law says that
these forces are equal
and opposite.
Adding force vectors
 Suppose
three people are
trying to keep an injured polar
bear in one place.
 The
bear will not move if the
net force (sum of all the forces)
is zero.
 To
find the answer, we need a
way to add vectors.
Adding force vectors
 On
a graph, you add vectors by drawing them to
scale at the correct angles and end to end.
 The
total of all the vectors is called the resultant.
Finding tension forces
A monkey hangs from two ropes. The weight of the
monkey is 135 N. The tension force from one of
the ropes is 110 N, exerted at an angle of 55°.
What is the tension force exerted by the other
rope on the monkey?
1.
2.
3.
Looking for: … an unknown force (F1) exerted by a rope.
Given: … the monkey’s weight (Fw = 135 N) and the
tension force (F2 = 110 N) and angle of the other rope (55o).
Relationships: The net force on the monkey is zero.
Finding tension forces
What is the tension force
exerted by the other rope
on the monkey?
4.
Solution: Find the x- and y-components of F2 by graphing
the force. Using the graph, you find that the components
are (63, 90). Now that you know the components of two of
the forces, find the third force:
(63, 90) + (0, –135) + (x, y) = 0
(x, y) for F1= (–63, 45)
Plot the x-and y-components for F1. Draw the vector to find a
force of 77 N.
The force from a spring

Springs are used in many devices to
keep objects in equilibrium or cause
acceleration.

The most common type of spring is a
coil of metal or plastic that creates a
force when you stretch it or compress
it.

Newton’s third law explains why a
spring’s force acts opposite to the
direction it is stretched or compressed.
Normal force and spring

How does a table “know” how much normal force to supply to
keep a book at rest?

Matter in the table acts like a collection of very stiff
compressed springs.

The amount of compression is so small you cannot see it, but
it can be measured with sensitive instruments.
Hooke’s Law
 Hooke’s
law states that
the force exerted by a
spring is proportional to
its change in length.
 Some
springs exert small forces and are easy to
stretch.
 The
relationship between the force exerted by a
spring and its change in length is called the spring
constant.
Hooke’s law
 When
a hanging scale weighs an object, the distance
the spring stretches is proportional to the object’s
weight. An object that is twice as heavy changes the
spring’s length twice as much.
 The
force exerted by a spring is directly related to the
spring constant multiplied by the displacement of the
spring.
 There
is a negative sign on the right-hand side of the
equation because the force of the spring always acts
in a direction opposite to the displacement.
Unit 2: Forces
Chapter 5: Forces in Equilibrium
 5.1
The Force Vector
 5.2
Forces and Equilibrium
 5.3
Friction
 5.4
Torque and Rotational Equilibrium
5.3 Investigation: Friction
Key Question:
What happens to the force of sliding friction as you add
mass to a sled?
Objectives:

Determine the force of friction present when Energy Car
sleds of different masses are launched and move along the
SmartTrack.

Calculate the coefficient of sliding friction
Friction
 Friction
is a force that results from relative motion
between objects.
 Friction
resists the motion of objects or surfaces due
to the microscopic hills and valleys that come into
contact with each other.
Friction
 Because
friction exists in many
different situations, it is
classified into several types.
 Sliding
friction is present when
two objects or surfaces slide
across each other.
 Static
friction exists when
forces are acting to cause an
object to move but friction is
keeping the object from moving.
Friction forces
 Friction
is a force, measured
in newtons just like any other
force.
 You
draw the force of friction
as another arrow on a freebody diagram.
 The
force of friction acting on
a surface always acts opposite
to the direction of motion of
that surface.
Identifying friction forces

It is harder to get something
moving than it is to keep it
moving.

The reason is that static friction
is greater than sliding friction for
almost all combinations of
surfaces.

To keep a box moving at
constant speed you must push
with a force equal to the force of
sliding friction.
A model for friction
 No
one model or formula
can accurately describe the
many processes that
create friction.
 The
greater the force
squeezing two surfaces
together, the greater the
friction force.
Reducing the force of friction
 A fluid
used to reduce friction
is called a lubricant.
 You
add oil to a car engine so
that the pistons will slide back
and forth with less friction.
 Another
method of reducing
friction is to separate the two
surfaces with a cushion of air.
Using friction

The brakes on some bicycles create friction
between two rubber brake pads and the rim
of the wheel.

Rain and snow act like lubricants to separate
tires from the road.

Friction is the force that keeps nails in place.

Shoes are designed to increase the friction
between their soles and the ground.
Unit 2 Forces
Chapter 5 Forces in Equilibrium
 5.1
The Force Vector
 5.2
Forces and Equilibrium
 5.3
Friction
 5.4
Torque and Rotational Equilibrium
Torque
 Torque
is a measure of how
much a force acting on an
object causes the object to
rotate.
 Torque
causes objects to
rotate or spin.
 Torque
is the rotational
equivalent of force.
The canoe rotates
counterclockwise hits
both docks if the forces
are applied accordingly.
Torque
 The
line about which an object
turns is its axis of rotation.
 Some
objects have a fixed axis.
 A door’s
axis is fixed at the
hinges.
 Doorknobs
are positioned far
from the hinges to provide the
greatest amount of torque.
Torque
 Torque
is created whenever the line of action of a
force does not pass through the axis of rotation.
 The
line of action is an imaginary line in the direction
of the force and passing through the point where the
force is applied.
If the line of action passes
through the axis, the torque is
zero.
Calculating torque
 The
torque created by a force depends on the
strength of the force and also on the lever arm.
 The
lever arm is the perpendicular distance between
the line of action of the force and the axis of rotation.
Torque and direction
 The
direction of torque is  Positive torque is
often drawn with a
counterclockwise, and
circular arrow showing
negative torque is
how the object would
clockwise..
rotate.
Torque and force differ
 Torque
is created by force, but it is not the same
thing as force.
 Torque
depends on both force and distance.
 Torque
(N·m) has different units from force (N).
 The
same force can produce any amount of torque
depending on where, and in what direction, it is
applied.
Torque and force
 The
same force can
create different
amounts of torque
depending on where it
is applied and in what
direction.
 Some
forces produce
no torque.
Net torque
 If
more than one torque acts on
an object, the torques combine
to equal the net torque.
 If
the torques make an object
spin in the same direction, they
are added.
 If
the torques make the object
spin in opposite directions, the
torques are subtracted.
Calculating torque
A force of 50 N is applied to a wrench that is 0.30 m.
long. Calculate the torque if the force is applied
perpendicular to the wrench.
1.
Looking for: … the torque.
2.
Given: … the force (50 N) and the length
of the lever arm (0.30 m)
3.
Relationships: Use: τ = Fr
4.
Solution: τ = (0.30 m)(50 N) = 15 N·m
Rotational
equilibrium
 An
object is in rotational equilibrium when the net
torque applied to it is zero.
 Rotational
equilibrium is often used to determine
unknown forces.
 Any
object that is not moving must have a net torque
of zero and a net force of zero.
Applying rotational equilibrium

Triple beam balances used in schools and scales used in
doctors’ offices use balanced torques to measure weight.

When using such scales, you must slide small masses away
from the axis of rotation until the scale reaches equilibrium.

Moving the mass increases its lever arm and its torque.
Architecture: Forces in Equilibrium

Four thousand years ago, the builders of the Pyramids of Egypt
understood how a structure must be designed to remain standing.

Egyptians used trial-and-error along with back-breaking effort to
refine their design, keeping ideas that worked and discarding those
that didn’t.