* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 04-Statics, Torque, Rotational Motion
Electromagnetism wikipedia , lookup
Coriolis force wikipedia , lookup
Lorentz force wikipedia , lookup
Fictitious force wikipedia , lookup
Centrifugal force wikipedia , lookup
Torque wrench wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
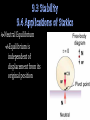
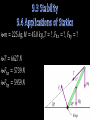
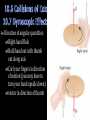
Physics Unit 4 This Slideshow was developed to accompany the textbook OpenStax Physics Available for free at https://openstaxcollege.org/textbooks/collegephysics By OpenStax College and Rice University 2013 edition Some examples and diagrams are taken from the textbook. Slides created by Richard Wright, Andrews Academy [email protected] Statics Study of forces in equilibrium Equilibrium means no acceleration First condition of equilibrium 𝑛𝑒𝑡 𝐹 = 0 𝐹𝑥 = 0 and 𝐹𝑦 = 0 They can still rotate, so… Think of opening a door Which opens the door the best? Picture a Big force large torque Force away from pivot large torque Force directed ⊥ to door large torque τ=F×r This means we use the component of the force that is perpendicular to the lever arm τ = F r τ = F r sin θ θ is the angle between the force and the radius Unit: Nm CCW + CW - You are meeting the parents of your new “special” friend for the first time. After being at their house for a couple of hours, you walk out to discover the little brother has let all the air out of one of your tires. Not knowing the reason for the flat tire, you decide to change it. You have a 50-cm long lug-wrench attached to a lugnut as shown. If 900 Nm of torque is needed, how much force is needed? F = 2078 N Less force required if pushed at 90° 120° Second condition of equilibrium Net torque = 0 A 5 m, 10 kg seesaw is balanced by a little girl (25 kg) and her father (80 kg) at opposite ends as shown below. How far from the seesaw’s center of mass must the fulcrum be placed? 80 kg 1.20 m xm 25 kg How much force must the fulcrum 10 kg support? 5m 1029 N Twist out the answers to these torque questions 9P1-5 Read 9.3, 9.4 9CQ6-8 Answers 1) 46.8 Nm 2) 23.1 Nm, 17.0 ft lb 3) 23.3 Nm 4) 568 N 5) 1.36 m, 686 N Stable equilibrium When displaced from equilibrium, the system experiences a net force or torque in a direction opposite to the direction of the displacement. Unstable equilibrium When displaced from equilibrium, the net force or torque is in same direction of the displacement Neutral Equilibrium Equilibrium is independent of displacement from its original position Problem-Solving Strategy for Static Equilibrium 1. Is it in equilibrium? (no acceleration or accelerated rotation) 2. Draw free body diagram 3. Apply ∑𝐹 = 0 and/or ∑𝜏 = 0 a. Choose a pivot point to simplify the problem 4. Check your solution for reasonableness. The system is in equilibrium. A mass of 225 kg hangs from the end of the uniform strut whose mass is 45.0 kg. Find (a) the tension T in the cable and the (b) horizontal and (c) vertical force components exerted on the strut by the hinge. Free body diagram next slide 𝑚 = 225 𝑘𝑔, 𝑀 = 45.0 𝑘𝑔, 𝑇 = ? , 𝐹ℎ𝑥 = ? , 𝐹ℎ𝑦 = ? 𝑇 = 6627 𝑁 𝐹ℎ𝑥 = 5739 𝑁 𝐹ℎ𝑦 = 5959 𝑁 Pick a stable position while you apply your knowledge. 9P6-7, 9, 11-13, 16-17 Read 9.5, 9.6 9CQ10-12, 15, 17, 19 Answers 6) 1.43 × 103 𝑁 7) 1.8 m 9) 392 N, 196 N 11) 11.0 N, 0.450 1 12) of the 6 weight, 2.0 × 104 N up 13) 7.20 × 103 𝑁, 65.2° 16) 1.11 × 103 𝑁 along each leg 17) 126 N, 751 N Machines make work easier Energy is conserved so same amount of energy with or without machine Mechanical Advantage (MA) 𝑀𝐴 = 𝐹𝑜 𝐹𝑖 Lever Uses torques with pivot at N 𝐹𝑖 𝑙𝑖 = 𝐹𝑜 𝑙𝑜 𝐹𝑜 𝐹𝑖 = 𝑙𝑖 𝑙𝑜 When F ↑, 𝑙 ↓ 𝑀𝐴 = 𝐹𝑜 𝐹𝑖 = 𝑑𝑖 𝑑𝑜 Other simple machines Wheel and Axle Lever Inclined Plane Ramp – less force to slide up, but longer distance Screw Inclined plane wrapped around a shaft Wedge Two inclined planes Pulley Grooved wheel Changed direction of force In combination, can decrease force What is the mechanical advantage of the inclined plane? MA = 10 What is the weight of the cart assuming no friction? 𝐹𝑜 = 500 N Muscles only contract, so they come in pairs Muscles are attached to bones close to the joints using tendons This makes the muscles supply larger force than is lifted Input force > output force MA < 1 Machines can’t help you much here, exercise your mental muscles instead 9P19-24, 29, 31-32, 34-35 Read 10.1, 10.2 10CQ1-4 Answers 19) 25.0, 50.0 N 20) 1.78 m 21) 18.5, 29.1 N, 510 N 22) 0.0400 23) 1.30 × 103 N 24) 564 N 29) 1.72 × 103 N 31) 470 N 32) 25 N down, 75 N up 34) 2.25 × 103 N 35) 1.2 × 102 N up, 84 N down Rotational motion Describes spinning motion 𝜃 is like x 𝑥 = 𝑟𝜃 position 𝜔 is like v Δ𝜃 𝜔 = Δ𝑡 𝑣 = 𝑟𝜔 velocity 𝛼 is like a Δ𝜔 𝛼 = Δ𝑡 𝑎𝑡 = 𝑟𝛼 acceleration Two components to acceleration Centripetal Toward center Changes direction only since perpendicular to v 𝑎𝑐 = 𝑣2 𝑟 Tangental (linear) Tangent to circle Changes speed only since parallel to v 𝑎𝑡 = 𝑟𝛼 Equations of kinematics for rotational motion are same as for linear motion 𝜃 = 𝜔𝑡 𝜔 = 𝜔0 + 𝛼𝑡 1 𝜃 = 𝜔0 𝑡 + 𝛼𝑡 2 2 𝜔2 = 𝜔02 + 2𝛼𝜃 Reasoning Strategy 1. Examine the situation to determine if rotational motion involved 2. Identify the unknowns (a drawing can be useful) 3. Identify the knowns 4. Pick the appropriate equation based on the knowns/unknwons 5. Substitute the values into the equation and solve 6. Check to see if your answer is reasonable A figure skater is spinning at 0.5 rev/s and then pulls her arms in and increases her speed to 10 rev/s in 1.5 s. What was her angular acceleration? 39.8 rad/s2 A ceiling fan has 4 evenly spaced blades of negligible width. As you are putting on your shirt, you raise your hand. It brushes a blade and then is hit by the next blade. If the blades were rotating at 4 rev/s and stops in 0.01 s as it hits your hand, what angular displacement did the fan move after it hit your hand? 𝜃 = 0.02 rev = 0.126 rad = 7.2° Spin up your mind and toss out some answers 10P1-2, 5-8 Read 10.3, 10.4 10CQ5-8, 10 Answers 1) 0.737 rev/s 2) 87.3 rad/s2, 8.29 m/s2, 1.04 × 107 m/s2, 1.06 × 106 𝑔 5) 80 rad/s2, 1.0 rev 6) 405 m 7) 45.7 s, 116 rev 8) -25.0 rad/s2, 28.7 rev, 3.80 s, 50.7 m, 26.6 m/s, reasonable 𝜏 = 𝐹𝑇 𝑟 𝐹𝑇 = 𝑚𝑎𝑡 𝜏 = 𝑚𝑎𝑡 𝑟 𝑎𝑡 = 𝑟𝛼 𝜏 = 𝑚𝑟 2 𝛼 𝐼 = 𝑚𝑟 2 Moment of inertia of a particle 𝜏 = 𝐼𝛼 Newton’s second law for rotation α is in rad/s2 Moment of Inertia (I) measures how much an object wants to keep rotating (or not start rotating) Use calculus to find 𝐼 = ∑𝑚𝑟 2 Unit: kg m2 Page 328 lists I for many different mass distributions Work for rotation 𝑊 = 𝐹Δ𝑠 𝑊 = Δ𝑠 𝐹𝑟 𝑟 𝑊 = 𝜏𝜃 Kinetic Energy 1 2 𝐾𝐸𝑟𝑜𝑡 = 𝐼𝜔2 Conservation of Mechanical Energy 𝑃𝐸𝑖 + 𝐾𝐸𝑖 = 𝑃𝐸𝑓 + 𝐾𝐸𝑓 Remember that the KE can include both translational and rotational. Zorch, an archenemy of Superman, decides to slow Earth’s rotation to once per 28.0 h by exerting an opposing force at and parallel to the equator. Superman is not immediately concerned, because he knows Zorch can only exert a force of 4.00×107 N (a little greater than a Saturn V rocket’s thrust). How long must Zorch push with this force to accomplish his goal? (This period gives Superman time to devote to other villains.) 1.26 × 1011 𝑦𝑟 A solid sphere (m = 2 kg and r = 0.25 m) and a thin spherical shell (m = 2 kg and r = 0.25 m) roll down a ramp that is 0.5 m high. What is the velocity of each sphere as it reaches the bottom of the ramp? Solid: 2.65 m/s Shell: 2.42 m/s Notice masses canceled so mass didn’t matter Don’t spin your wheels as you use energy to solve these problems 10P11-15, 22-26, 28, 30 Read10.5 10CQ13-14, 16, 18-20, 25-27 Answers 11) 0.363 𝑘𝑔 ⋅ 𝑚2 , 2.34 𝑘𝑔 ⋅ 𝑚2 12) 0.500 𝑘𝑔 ⋅ 𝑚2 13) 1.18 × 103 𝑁 14) 50.4 𝑁 ⋅ 𝑚, 17.1 𝑟𝑎𝑑/𝑠 2 , 17.0 𝑟𝑎𝑑/𝑠 2 15) 97.9 𝑟𝑎𝑑/𝑠 2 , 32.3 𝑚/𝑠, 0.817 s 22) 7.00 𝑚/𝑠 23) 2.57 × 1029 𝐽, 2.65 × 1033 𝐽 24) 8.09 × 103 𝐽 25) 434 𝐽 𝑚 26) 9.66 𝑟𝑎𝑑/𝑠, 10.1 𝑠 28) 2.18 𝑚, 3.27 𝑚 30) 41.1 𝑟𝑎𝑑/𝑠 2 , 15.7 𝐽 Linear momentum p = mv Angular momentum L = Iω Unit: kg m2/s ω must be in rad/s When you rotate something you exert a torque. More torque = faster change in angular momentum 𝜏𝑛𝑒𝑡 = Δ𝐿 Δ𝑡 Like 𝐹 = Δ𝑝 Δ𝑡 Linear momentum of a system is conserved if 𝐹𝑛𝑒𝑡 = 0 p0 = pf Angular momentum of a system is also conserved if 𝜏𝑛𝑒𝑡 = 0 L0 = Lf A 10-kg solid disk with r = 0.40 m is spinning at 8 rad/s. A 9-kg solid disk with r = 0.30 m is dropped onto the first disk. If the first disk was initially not rotating, what is the angular velocity after the disks are together? ω = 5.31 rad/s What was the torque applied by the first disk onto the second if the collision takes 0.01 s? 𝜏 = 215 Nm Angular Momentum conserved if net external torque is zero Linear Momentum conserved if net external force is zero Kinetic Energy conserved if elastic collision Direction of angular quantities Right-hand Rule Hold hand out with thumb out along axis Curl your fingers in direction of motion (you may have to turn your hand upside down) vector in direction of thumb A person is holding a spinning bicycle wheel while he stands on a stationary frictionless turntable. What will happen if he suddenly flips the bicycle wheel over so that it is spinning in the opposite direction? Gyroscopes Two forces acting on a spinning gyroscope. The torque produced is perpendicular to the angular momentum, thus the direction of the torque is changed, but not its magnitude. The gyroscope precesses around a vertical axis, since the torque is always horizontal and perpendicular to L. If the gyroscope is not spinning, it acquires angular momentum in the direction of the torque ( L = ΔL ), and it rotates around a horizontal axis, falling over just as we would expect. Let you momentum carry you through these problems 10P36-41 Read 10.6, 10.7 10CQ26-27, 29-30 Answers 36) 2.66 × 1040 𝑘𝑔 ⋅ 33 7.07 × 10 𝑘𝑔 ⋅ 𝑚2 𝑠 𝑚2 𝑠 39) 2.30 𝑟𝑎𝑑/𝑠 40) 25.3 rpm , 𝑚2 37) 2.89 × 10 𝑘𝑔 ⋅ , 𝑠 𝑚2 29 2.37 × 10 𝑘𝑔 ⋅ 𝑠 2 38) 22.5 𝑘𝑔 ⋅ 𝑚 /𝑠 34 𝑚2 41) 15.1 𝑘𝑔 ⋅ , 𝑠 2 1.92 𝑘𝑔 ⋅ 𝑚 , −0.503 𝑁 ⋅ 𝑚