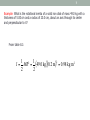* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download General Physics (PHY 2130)
Equations of motion wikipedia , lookup
Hunting oscillation wikipedia , lookup
Automatic transmission wikipedia , lookup
Virtual work wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Center of mass wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Coriolis force wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Transmission (mechanics) wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Differential (mechanical device) wikipedia , lookup
Fictitious force wikipedia , lookup
Centrifugal force wikipedia , lookup
Mitsubishi AWC wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Moment of inertia wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Torque wrench wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
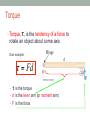
General Physics (PHY 2130) Lecture 19 • Rotational dynamics rotational kinetic energy torque moment of inertia http://www.physics.wayne.edu/~apetrov/PHY2130/ Lightning Review Last lecture: 1. Momentum: momentum conservation collisions in one and two dimensions Review Problem: A rider in a “barrel of fun” finds herself stuck with her back to the wall. Which diagram correctly shows the forces acting on her? Rotational kinetic energy and Inertia For a rotating solid body: n 1 2 1 1 1 2 2 2 K rot = m1v1 + m2v2 + … + mn vn = ∑ mi vi 2 2 2 i =1 2 vi ri vi = riω where ri is the distance from the rotation axis to the mass mi. n 1 1 ⎛ n 1 2 2 2 ⎞ 2 K rot = ∑ mi (riω ) = ⎜ ∑ mi ri ⎟ω = Iω 2 ⎝ i =1 2 i =1 2 ⎠ K rot 1 2 = Iω 2 n I = ∑ mi ri 2 i =1 I = rotational inertia or moment of inertia of the body about the axis SI unit of I = kg.m2 3 mi 4 Example: (a) Find the moment of inertia of the system below. The masses are m1 and m2 and they are separated by a distance r. Take m1 = 2.00 kg, m2 = 1.00 kg, r1= 0.33 m , and r2 = 0.67 m to compute the moment of inertia numerically. Assume the rod connecting the masses is massless. (b) What is the moment of inertia if the axis is moved so that is passes through m1? ω m1 ω r1 Solution: r2 m2 (a) Note that r1 and r2 are the distances between mass 1 and the rotation axis and mass 2 and the rotation axis (the dashed, vertical line) respectively. 2 I = ∑ mi ri2 = m1r12 + m2 r22 i=1 2 2 = ( 2.00 kg) ( 0.33 m ) + (1.00 kg) ( 0.67 m ) = 0.67 kg m 2 (b) If the axis is moved so that is passes through m1 then r1 and r2 would change 2 I = ∑ mi ri2 = m1r12 + m2 r22 i=1 2 2 = ( 2.00 kg) ( 0.00 m ) + (1.00 kg) (1.00 m ) = 1.00 kg m 2 Example: Moment of Inertia of a Uniform Ring • Image the hoop is divided into a number of small segments, m1 … • These segments are equidistant from the axis I = ∑ mi ri = ∑ mi R 2 i =R i 2 ∑ m = MR i i 2 2 6 7 Example: What is the rotational inertia of a solid iron disk of mass 49.0 kg with a thickness of 5.00 cm and a radius of 20.0 cm, about an axis through its center and perpendicular to it? From table 8.1: 1 1 2 2 I = MR = (49.0 kg )(0.2 m ) = 0.98 kg m 2 2 2 Total Energy of Rotating System • An object rotating about some axis with an angular speed, ω, has rotational kinetic energy ½Iω2 • Energy concepts can be useful for simplifying the analysis of rotational motion • Conservation of Mechanical Energy ( KEt + KEr + PE g )i = ( KEt + KEr + PE g ) f • Remember, this is for conservative forces, no dissipative forces such as friction can be present ConcepTest A force F is applied to a dumbbell for a time interval Δt, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater energy? 1. 2. 3. 4. (a) (b) no difference The answer depends on the rotational inertia of the dumbbell. ConcepTest A force F is applied to a dumbbell for a time interval Δt, first as in (a) and then as in (b). In which case does the dumbbell acquire the greater energy? 1. 2. 3. 4. (a) (b) no difference The answer depends on the rotational inertia of the dumbbell. Since CM speeds are the same, translational kinetic energies are the same. But (b) also rotates, so it also has rotational energy. Torque • Consider force required to open door. Is it easier to open the door by pushing/pulling away from hinge or close to hinge? Farther from from hinge, larger rotational effect! Physics concept: torque close to hinge away from hinge Torque τ • Torque, , is the tendency of a force to rotate an object about some axis Door example: τ = Fd • τ is the torque • d is the lever arm (or moment arm) • F is the force Lever Arm • The lever arm, d, is the shortest (perpendicular) distance from the axis of rotation to a line drawn along the the direction of the force • d = L sin Φ • It is not necessarily the distance between the axis of rotation and point where the force is applied Direction of Torque • Torque is a vector quantity • The direction is perpendicular to the plane determined by the lever arm and the force • Direction and sign: Direction of torque: out of page If the turning tendency of the force is counterclockwise, the torque will be positive If the turning tendency is clockwise, the torque will be negative SI Units Newton meter (Nm) US Customary Foot pound (ft lb) An Alternative Look at Torque • The force could also be resolved into its x- and ycomponents • The x-component, F cos Φ, produces 0 torque • The y-component, F sin Φ, produces a non-zero torque τ = FL sin φ F is the force L is the distance along the object Φ is the angle between force and object L ConcepTest You are trying to open a door that is stuck by pulling on the doorknob in a direction perpendicular to the door. If you instead tie a rope to the doorknob and then pull with the same force, is the torque you exert increased? Will it be easier to open the door? 1. No 2. Yes ConcepTest You are trying to open a door that is stuck by pulling on the doorknob in a direction perpendicular to the door. If you instead tie a rope to the doorknob and then pull with the same force, is the torque you exert increased? Will it be easier to open the door? 1. No 2. Yes 19 Example: The pull cord of a lawnmower engine is wound around a drum of radius 6.00 cm, while the cord is pulled with a force of 75.0 N to start the engine. What magnitude torque does the cord apply to the drum? F=75 N τ = r⊥ F = rF R=6.00 cm = (0.06 m )(75.0 N ) = 4.5 Nm ConcepTest You are using a wrench and trying to loosen a rusty nut. Which of the arrangements shown is most effective in loosening the nut? List in order of descending efficiency the following arrangements: ConcepTest You are using a wrench and trying to loosen a rusty nut. Which of the arrangements shown is most effective in loosening the nut? List in order of descending efficiency the following arrangements: 2, 1, 4, 3 or 2, 4, 1, 3 What if two or more different forces act on lever arm? Net Torque • The net torque is the sum of all the torques produced by all the forces • Remember to account for the direction of the tendency for rotation • Counterclockwise torques are positive • Clockwise torques are negative Example 1: N Determine the net torque: 4m 2m Given: weights: w1= 500 N w2 = 800 N lever arms: d1=4 m d2=2 m Find: Στ = ? 500 N 800 N 1. Draw all applicable forces 2. Consider CCW rotation to be positive ∑τ = (500 N )(4 m) + (−)(800 N )(2 m) = +2000 N ⋅ m − 1600 N ⋅ m = +400 N ⋅ m Rotation would be CCW Where would the 500 N person have to be relative to fulcrum for zero torque? Example 2: N’ d2 m y 2m Given: weights: w1= 500 N w2 = 800 N lever arms: d1=4 m Στ = 0 Find: d2 = ? 500 N 800 N 1. Draw all applicable forces and moment arms ∑τ ∑τ RHS = − (800 N )(2 m) LHS = (500 N )(d 2 m) −800 ⋅ 2 [ N ⋅ m] + 500 ⋅ d 2 [ N ⋅ m] = 0 ⇒ d 2 = 3.2 m According to our understanding of torque there would be no rotation and no motion! What does it say about acceleration and force? ∑ F =(−500 N ) + N '+(−800 N ) = 0 i Thus, according to 2nd Newton’s law ΣF=0 and a=0! N ' = 1300 N 27 Calculating Work done from the Torque The work done by a torque τ is W = τΔθ . where Δθ is the angle (in radians) the object turns through. 28 Example: A flywheel of mass 182 kg has a radius of 0.62 m (assume the flywheel is a hoop). (a) What is the torque required to bring the flywheel from rest to a speed of 120 rpm in an interval of 30 sec? (b) How much work is done in this 30 sec period? (a) Let’s recall the definition of force and angular acceleration ω f = 120 rev ⎛ 2π rad ⎞⎛ 1 min ⎞ ⎜ ⎟⎜ ⎟ = 12.6 rad/sec min ⎝ 1 rev ⎠⎝ 60 sec ⎠ ⎛ Δω ⎞ τ = rF = r (ma ) = rm(rα ) = mr ⎜ ⎟ ⎝ Δt ⎠ ω f − ωi ⎞ ω f ⎞ 2 ⎛ 2 ⎛ ⎟⎟ = mr ⎜⎜ ⎟⎟ = 29.4 Nm = mr ⎜⎜ ⎝ Δt ⎠ ⎝ Δt ⎠ 2 (a) Use the definition of work for rotational motion: W = τΔθ = τ (ωav Δt ) ⎛ ωi + ω f = τ ⎜⎜ ⎝ 2 ⎞ ⎛ ω f ⎟⎟Δt = τ ⎜⎜ ⎠ ⎝ 2 ⎞ ⎟⎟Δt = 5600 J ⎠