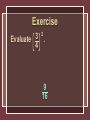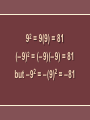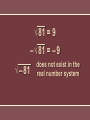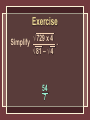Download File - Mrs. Hille`s FunZone

Exercise
Evaluate 32.
9
Exercise
Evaluate (3 + 4)2.
49
Exercise
Evaluate 32 + 42.
25
Exercise
Evaluate 3
4
2
.
9
16
Exercise
2
3
Evaluate 2 .
4
9
16
Square Root
The square root of x is a
number whose product when
multiplied by itself is x.
2
9
2
(– 9)
= 9(9) = 81
= (– 9)(– 9) = 81
but – 92 = – (9)2 = – 81
√ 81 = 9
– √ 81 = – 9
√ – 81
does not exist in the
real number system
Example 1
Find √ 25 .
5
Example 1
Find – √ 49 .
–7
Example
State whether √ 144 is an
integer, real, or not real.
integer
Example
State whether √ 132 is an
integer, real, or not real.
real
Example
State whether √ –36 is an
integer, real, or not real.
not real
12 = 1
62 = 36
112 = 121 162 = 256
22 = 4
72 = 49
122 = 144 172 = 289
32 = 9
82 = 64
132 = 169 182 = 324
42 = 16
92 = 81
142 = 196 192 = 361
52 = 25 102 = 100 152 = 225 202 = 400
These are called
“perfect squares.”
4
√ 16 = 4 =
1
rational
number
If x is not a perfect
square then √ x is an
irrational number.
√ 5 is 2.236067977…
You can estimate √ x by
finding the two perfect
squares between
which x lies.
Example 2
Between what two
consecutive integers does
√ 32 lie?
25 < 32 < 36
√ 25 < √ 32 < √ 36
5 < √ 32 < 6
√ 32 is between 5 and 6.
Guess and Check Method:√ 19
16 < 19 < 25
√ 16 < √ 19 < √ 25
4 < √ 19 < 5
Estimate √ 19 ≈ 4.2 4.22 = 17.64
Estimate √ 19 ≈ 4.3 4.32 = 18.49
Estimate √ 19 ≈ 4.4 4.42 = 19.36
4.3 < √ 19 < 4.4 and √ 19 ≈ 4.4
Example 3
Estimate √ 47 to the nearest
tenth.
36 < 47 < 49
√ 36 < √ 47 < √ 49
6 < √ 47 < 7
Estimate √ 47 to the nearest
tenth.
6.92 = 47.61
0.61 greater than 47
6.82 = 46.24
0.76 less than 47
√ 47 ≈ 6.9
Example
Order the following numbers
from smallest to largest
using the < symbol:
11.7, 11.5, √ 135, √ 139.
11.5 < √ 135 < 11.7 < √ 139
Example
Determine what integers a2
lies between if a is any
single-digit integer.
0 and 100
Example
Determine what integers a2
lies between if a is any twodigit integer.
100 and 10,000
Example
Estimate √ 53 by finding the
two consecutive integers it
lies between.
7 and 8
Example
Estimate √ 53 by finding its
decimal approximation to
the nearest integer.
7
Example
Estimate √ 53 by finding its
decimal approximation to
the nearest tenth.
7.3
Example
Estimate √ 53 by finding its
decimal approximation to
the nearest hundredth.
7.28
√x + √y
Simplify each square root
before adding.
√x + y
Simplify by taking the
square root after adding.
Example 4
Simplify √ 64 + √ 25.
√ 64 + √ 25 = 8 + 5
= 13
Example 4
Simplify √ 72 – 23.
√ 72 – 23 = √ 49
=7
Order of Operations
1. Symbols of Grouping—
evaluate quantities within
symbols of grouping first.
2. Exponents and radicals—
evaluate a term with an
exponent or square root
before performing other
operations.
Order of Operations
3. Multiplication and
division—perform these
operations in order from left
to right.
4. Addition and subtraction—
perform these operations
last, in order from left to
right.
Example 5
Simplify –4 √ 116 – 35.
– 4 √ 116 – 35 = –4 √ 81
= –4(9)
= –36
Example
Simplify 2 √ 80 + 64.
24
Example
Simplify 3 √ 25 – 2 √ 64.
–1
Example
3(
√
121
+
√
81)
Simplify
.
4 √ 100 – 64
5
2
Exercise
√
729
x
4
Simplify
.
√ 81 – √ 4
54
7