Download Bild 1

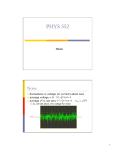
LECTURE 8:
OSCILLATORS
NOISE IN ELECTRONIC SYSTEMS
Oscillators
Wien-Bridge
Relaxation Oscillator
Noise
Noise
Type of Noise
Noise Sources
Noise Analysis
OSCILLATORS
An oscillator is a circuit that produces a periodically
oscillating waveform on its output with dc input.
Two major classifications:
o Feedback oscillators
o Relaxation oscillators
FEEDBACK OSCILLATORS
Feedback oscillator operation is based on the
principle of positive feedback.
A fraction of output signal is returned to input with
no net phase shift resulting in a re-inforcement
of the output signal.
FEEDBACK OSCILLATORS
Conditions of Oscillations:
i.
The phase shift around the feedback loop must
be 0 degree.
ii.
Closed feedback loop gain Acl must be 1.
FEEDBACK OSCILLATORS
Vf is amplified to produce the output
voltage , which in turn produces the
feedback voltage.
A loop is created and signal sustain itself
and produces continuous oscillations.
In some types of oscillators feedback
shifts the phase by 180. inverting amplifier
are used there to produce another 180
degree
START-UP CONDITIONS
 Feedback oscillators require a small disturbance such as that
generated by thermal noise to start oscillations.
 This initial voltage starts the feedback process and oscillations.
 The feedback circuit permits only a voltage with a frequency equal to
selected frequency to appear in phase on the amplifier’s input.
WIEN-BRIDGE OSCILLATORS
RC feedback is used in various lower frequency (up to 1 MHz) sinewave oscillators.
At resonant frequency fr the attenuation of the circuit is 1/3.
The lead-lag circuit is used in the feedback of Wien-Bridge
oscillator.
It gives 0 phase shift and 1/3 attenuation at resonant frequency.
WIEN-BRIDGE OSCILLATORS
The basic Wien-bridge uses the lead-lag network to select a
specific frequency that is amplified. The voltage-divider sets the
gain to make up for the attenuation of the feedback network.
The non-inverting amplifier must
Voltagehave a gain of exactly 3.0 as set by divider
R1 and R2 to make up for the
attenuation.
If it is too little, oscillations will not
occur; if it is too much the sine
wave will be clipped.
R1
–
Vout
R2
+
R3
C1
C2
R4
Lead-lag
network
Basic Circuit Wien Bridge Oscillator
WIEN-BRIDGE OSCILLATION
CONDITIONS
The phase shift around the positive feedback loop must be 0o and
the gain around the loop must be 1.
The 0o phase-shift
condition is met when
the frequency is fr.
WIEN-BRIDGE OSCILLATOR
STARTUP
The loop gain should be greater than 1 at startup to build up output.
WIEN-BRIDGE OSCILLATOR
STARTUP
RELAXATION OSCILLATOR
A simple relaxation oscillator that uses a Schmitt trigger is the basic
square-wave oscillator.
The two trigger points, UTP and LTP are set by R2 and R3. The
capacitor charges and discharges between these levels:
VUTP
R1
 R3 
 Vmax 

 R2  R3 
 R3 
VLTP  Vmax 

 R2  R3 
VC
–
Vout
C
+
Vf
R2
The period of the waveform is
given by:
 2R 
T  2 R1C ln 1  3 
R2 

R3
NOISE
Noise is a random fluctuation in an electrical signal.
Noise in electronic devices varies greatly, as it can be produced by
several different effects.
Noise is a fundamental parameter to be considered in an electronic
design as it typically limits the overall performance of the system.
Noise is a purely random signal, the instantaneous value and/or
phase of the waveform cannot be predicted at any time.
The amplitude of the signal has very nearly a Gaussian probability
density function.
EXTERNAL AND INTERNAL NOISE
Noise can either be generated internally in the
op amp, from its associated passive
components, or superimposed on the circuit by
external sources.
“External” refers to noise present in the signal
being applied to the circuit or to noise
introduced into the circuit by another means,
such as conducted on a system ground or
received on one of the many antennas formed
by the traces and components in the system.
TYPES OF INTERNAL NOISE





Thermal Noise
Shot Noise
Flicker Noise
Burst Noise
Avalanche Noise
Some or all of these noises may be present in a design, presenting a
noise spectrum unique to the system.
It is not possible in most cases to separate the effects, but knowing
general causes may help the designer optimize the design,
minimizing noise in a particular bandwidth of interest.
THERMAL NOISE
Generated by the random thermal motion of charge carriers
(usually electrons), inside an electrical conductor.
It happens regardless of any applied voltage.
 Power Spectral Density is nearly equal throughout
the frequency spectrum, approximately white noise.
THERMAL NOISE
The RMS voltage due to thermal noise , generated in a
resistance R (ohms) over bandwidth Δf (hertz), is given by:
The noise from a resistor is proportional to its resistance and
temperature.
Lowering resistance values also reduces thermal noise.
See example in section 10.3.2 ‘Op-amp for every one’
SHOT NOISE
The name ‘Shot Noise’ is short of Schottky noise, also called
quantum noise.
It is caused by random fluctuations in the motion of charge
carriers in a conductor.
SHOT NOISE
Some characteristics of shot noise:
 Shot noise is always associated with current flow. It stops
when the current flow stops.
 Shot noise is independent of temperature.
Shot noise is spectrally flat or has a uniform power density,
meaning that when plotted versus frequency it has a constant
value.
Shot noise is present in any conductor
FLICKER NOISE
Flicker noise is also called 1/f noise. Its origin is one of the
oldest unsolved problems in physics.
It is present in all active and many passive devices.
It may be related to imperfections in crystalline structure of
semiconductors, as better processing can reduce it.
FLICKER NOISE
Some characteristics of flicker noise:
 It increases as the frequency decreases, hence the name 1/f
 It is associated with a dc current in electronic devices
 It has the same power content in each octave (or decade)
BURST NOISE
Burst noise consists of sudden step-like transitions between
two or more levels.
is related to imperfections in semiconductor material and
heavy ion implants.
As high as several hundred microvolts.
Lasts for several milli-seconds.
Burst noise makes a popping sound at rates below 100 Hz
when played through a speaker — it sounds like popcorn
popping, hence also called popcorn noise.
 Low burst noise is achieved by using clean device
processing, and therefore is beyond the control of the designer.
AVALANCHE NOISE
Avalanche noise is created when a PN junction is operated in
the reverse breakdown mode.
Under the influence of a strong reverse electric field within the
junction’s depletion region, electrons have enough kinetic
energy.
They collide with the atoms of the crystal lattice, to form
additional electron-hole pair.
These collisions are purely random and produce random
current pulses similar to shot noise, but much more intense.
AVALANCHE NOISE
When electrons and holes in the depletion region of a
reversed-biased junction acquire enough energy to cause the
avalanche effect, a random series of large noise spikes will be
generated.
The magnitude of the noise is difficult to predict due to its
dependence on the materials.
MEASURING NOISE
RMS, P-P or PDF
Instantaneous noise voltage amplitudes are
as likely to be positive as negative.
Noise values form a random pattern
centered on zero.
Since amplitudes vary randomly with time,
they can only be specified by a probability
density function, most commonly by
Gaussian density function.
σ is the standard deviation of the Gaussian
distribution and the rms value of the noise
voltage and current.
The instantaneous noise amplitude is within 168% of the time, is within
±3σ of the mean 99.7% of the time and within ±3.4σ 99.94% of the time.
SIGNAL TO NOISE RATIO
The noisiness of a signal is defined as:
In other words, it is a ratio of signal voltage to noise voltage
(hence the name signal-to-noise ratio).
MULTIPLE NOISE SOURCES
When there are multiple noise sources in a circuit, the total root-meansquare (rms) noise signal is the square root of the sum of the average
mean-square values of the individual sources:
If there are two noise sources of equal amplitude in the circuit, the
total noise is not doubled (increased by 6 dB).
It only increases by 3 dB. Consider a very simple case, two noise
sources with amplitudes of 2 Vrms:
NOISE UNIT
Internal noise is normally specified as a noise
spectral density in rms volts or amps per root
Hertz, V/√Hz or A /√ Hz.
In datasheet it is often expressed with a plot:
Example:
An op-omp TLE2027 has noise specification of 2.5
nV/ √ Hz
Noise characteristic for TLE2027
http://www.ti.com/lit/ds/symlink/tle2027.pdf
EQUIVALENT NOISE EIN
TLE2027 is used in a system that operates
over an audio frequency range of 20 Hz to
20 kHz with a gain of 40db (100).
Equivalent noise over the whole bandwidth
is :
2.5nV * 20000 − 20
2.5nV * 141.35
EIN = 353.38nV
If the gain of the system is 100
Eout= 353.38nV x 100 = 35.3 microV
Noise characteristic for TLE2027
CALCULATING SNR
If the output signal is of 1V
SNR = 1V/ 35.3 uV
= 28328
SNRdB= 20log(28328)
= 89 dB
Noise characteristic for TLE2027
CORNER FREQUENCY NOISE IN
SPECTRAL DENSITY
Usually a plot for Noise Spectral
Density is given in op-amp datasheets.
These graphs usually show two distinct
regions:
o Lower frequencies where pink noise
is the dominant effect
o Higher frequencies where white noise
is the dominant effect
The point in the frequency spectrum where 1/f noise and white noise are
equal is referred to as the noise corner frequency, fnc
CORNER FREQUENCY IN NOISE
SPECTRAL DENSITY
The point in the frequency spectrum where 1/f
noise and white noise are equal is referred to
as the noise corner frequency, fnc
Pink noise
The fnc can be determined visually from the
graph:
Take the white noise portion of the curve, and
extrapolate it down to 10 Hz as a horizontal
line.
White noise
Take the portion of the pink noise from 10 Hz to 100 Hz, and extrapolate
it as a straight line.
The point where the two intercept is fnc, the point where the white noise
and pink noise are equal in amplitude.
CORNER FREQUENCY
Once the corner frequency is known, the
individual noise components can be added
together (if the bandwidth includes corner
frequency):
If fnc is not included in bandwidth, all of the contribution will be from either
the 1/f noise or the white noise.
Similarly, if the bandwidth is very large, and extends to three decades or so
above fnc, the contribution of the 1/f noise can be ignored.
OP-AMP CIRCUIT NOISE
MODEL
Noise in op-amp circuits can be modeled as
voltage noise source and current noise source.
Input voltage noise is always represented by a
voltage source in series with the non-inverting
input.
Input current noise is always represented by
current sources from both inputs to ground.
INVERTING OP-AMP CIRCUIT
NOISE MODEL
e2
e1
e3
R1
R2
Sources e1, e2 and e3
represent the thermal noise
contribution from the resistors.
E0
Note: Noise current sources are missing
here.
NONINVERTING OP AMP CIRCUIT
NOISE MODEL
Sources e1, e2 and e3
represent the thermal noise
contribution from the resistors.
Note: Noise current sources are missing
here.
GENERAL NOISE MODEL
Figure describes the noise model for
the non-inverting amplifier
configuration showing all noise
sources.
Input Noise expression:
eni=
In addition to the intrinsic input
voltage noise (en) and current noise
(in=in+=in-) sources, there also exists
thermal voltage noise (et 4 TR = k )
associated with each of the external
resistors.
(𝑒𝑛2 +4𝑘𝑇(𝑅𝑔||𝑅𝑓) + (𝑖𝑛 − 𝑅𝑓 𝑅𝑔
2
NON-INVERTING NOISE
MODEL
Adding input noise from
signal source at noninverting input:
Output Noise expression:
Eo=
𝑒𝑛 1 +
𝑅𝑓
𝑅𝑔
2
+ 𝐸𝑖𝑛 1 +
𝑅𝑓
𝑅𝑔
2
+
4𝑘𝑇𝑅𝑓
2
+
𝑅
4𝑘𝑇𝑅𝑔 ( 𝑓 )
𝑅𝑔
2
+ (𝑖𝑛 − 𝑅𝑓 𝑅𝑔 (𝑅𝑓 )
𝑅𝑔
2
INVERTING NOISE MODEL
Adding input noise from
signal source at inverting
input:
Output Noise expression:
Eo=
𝑒𝑛 1 +
𝑅𝑓
𝑅𝑔
2
+ 𝐸𝑖𝑛
𝑅𝑓
𝑅𝑔
2
+
4𝑘𝑇𝑅𝑓
2
+
𝑅
4𝑘𝑇𝑅𝑔 ( 𝑓 )
𝑅𝑔
2
+ (𝑖𝑛 − 𝑅𝑓 𝑅𝑔 (𝑅𝑓 )
𝑅𝑔
2
REDUCING RESISTANCE
VALUES
Reducing resistance value can help in reducing thermal noise.
THANK YOU