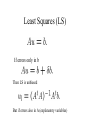Download Probability Review

Probability Review
(many slides from Octavia Camps)
Intuitive Development
• Intuitively, the probability of an event a
could be defined as:
Where N(a) is the number that event a happens in n trials
More Formal:
• W is the Sample Space:
– Contains all possible outcomes of an experiment
• w2 W is a single outcome
• A 2 W is a set of outcomes of interest
Independence
• The probability of independent events A, B
and C is given by:
P(ABC) = P(A)P(B)P(C)
A and B are independent, if knowing that A has happened
does not say anything about B happening
Conditional Probability
• One of the most useful concepts!
W
B
A
Bayes Theorem
• Provides a way to convert a-priori
probabilities to a-posteriori probabilities:
Using Partitions:
• If events Ai are mutually exclusive and
partition W
W
B
Random Variables
• A (scalar) random variable X is a function
that maps the outcome of a random event
into real scalar values
W
X(w)
w
Random Variables Distributions
• Cumulative Probability Distribution (CDF):
• Probability Density Function (PDF):
Random Distributions:
• From the two previous equations:
Uniform Distribution
• A R.V. X that is uniformly distributed
between x1 and x2 has density function:
X1
X2
Gaussian (Normal) Distribution
• A R.V. X that is normally distributed has
density function:
m
Statistical Characterizations
• Expectation (Mean Value, First Moment):
•Second Moment:
Statistical Characterizations
• Variance of X:
• Standard Deviation of X:
Mean Estimation from Samples
• Given a set of N samples from a
distribution, we can estimate the mean of
the distribution by:
Variance Estimation from
Samples
• Given a set of N samples from a
distribution, we can estimate the variance of
the distribution by:
Image Noise Model
• Additive noise:
Iˆ(i, j )  I (i, j ) N (i, j )
– Most commonly used
Additive Noise Models
• Gaussian
– Usually, zero-mean, uncorrelated
•Uniform
Measuring Noise
• Noise Amount: SNR = s/ n
• Noise Estimation:
– Given a sequence of images I0,I1, … IN-1
N 1
1
I (i, j ) 
N
I
 (i, j ) 
1 N 1
2
(
I
(
i
,
j
)

I
(
i
,
j
)
)

k
N  1 k 0
 n
1
RC
k 0
R 1 C 1
k
(i, j )
  (i, j )
i 0 j 0
Good estimators
Data values z are random variables
A parameter q describes the distribution
We have an estimator j (z) of the unknown parameter q.
If
E(j (z)  q )  0
or
E(j (z) ) = E(q) the estimator j (z) is unbiased
Balance between bias and
variance
Mean squared error as performance criterion
Least Squares (LS)
If errors only in b
Then LS is unbiased
But if errors also in A (explanatory variables)
Errors in Variable Model
Least Squares (LS)
bias
Larger variance in dA,,ill-conditioned A,
u oriented close to the eigenvector of the
smallest eigenvalue increase the bias
Generally underestimation
Estimation of optical flow
(a)
(b)
(a) Local information determines the component of flow perpendicular to edges
(b) The optical flow as best intersection of the flow constraints is biased.
Optical flow
I xu  I y v   I t
• One patch gives a system:
 I x1 I y1 
 I t1  0
I



0 
I
I
u
y2     t2 
 x2
 


 
   v     0


   
I
I
 xn
 I tn1  0
yn 

 
I su  I t  0
Noise model
• additive, identically, independently distributed,
symmetric noise:
I xi  I xi  N xi
I yi  I yi  N yi
I ti  I ti  N ti
E ( N xi N xi )  E ( N yi N yi )  
2
s
E ( N ti N ti )  
2
t