* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Optical Tweezers
Bohr–Einstein debates wikipedia , lookup
Cross section (physics) wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Particle in a box wikipedia , lookup
Atomic theory wikipedia , lookup
Identical particles wikipedia , lookup
Double-slit experiment wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
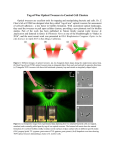
Optical Tweezers Charlie Mueller Jesse Fogleman Qualitative Description In a nutshell , optical tweezers all ow us the abili ty to remotely control matter with the use of lasers. The idea of moving matter with li ght is not new. Johannes Kepler observed that the tail s of comets were always pointing away from the Sun. Kepler knew that the Sun had to be exerting some kind of radiant pressure but could not verify this. Four centuries later, the idea of using li ght to move matter had become a reali ty and quantum mechanics helps us understand how. Light is able to move matter because photons carry momentum. A photon with any wavelength carries a momentum p h ( h is PlanckΥs constant). This means that when an atom emi ts or absorbs a photon itΥs momentum changes, in accordance with NewtonΥs laws. Along the same li nes, when a particle changes the direction of a beam of li ght as a result of reflection or refraction, it experiences a force. The first optical traps were used in 1970 at the AT&T Bell labs in the United States. The early traps levitatedΣ the particle by balancing the force of gravity or made use of two counter-propagating beams to trap the particles. In 1986, it was discovered that gradient forces alone would suffice in trapping a particle. Now, only a tightly focused single beam was required to hold and move a particle in three dim ensions. Qualitative Description 2 How do you focus a single laser beam? Pass it through a mi croscopeΥs objective lens! The mi croscope objective must have a high numerical aperture (a measure of the angle at which the beam approaches the focal point). This tightly focuses the beam so the gradient to trap the particle is effectively strong enough. The same lens may then be used to image the trapped particle, usua lly routed to a monitor. A laser with only a milli watt of power is necessary to trap a single, transparent particle. Optical tweezers exploit a refractive index mi smatch. Transparent particles have a higher refractive index than their surr oundings and are attracted to area of maximum intensity where the beam is most tightly focused, known as the beam waist. By moving the focus of the laser beam around a li ttle, dielectric and biological particles can be grabbed and moved in three dimensions. How big of a particle can the beam handle? Although the optical force of the tweezers is only on the order of piconewtons, this is suitable enough to move particles from tens of nanometers all the way up to tens of mi crons, because at the mi cro-level the optical forces are usua lly supreme. DNA, itΥs proteins and enzymes are most commonly manipulated with optical tweezers. Ray Tracing Analysis of Force Trap 1 sin(i ) 2 sin( r ) 2 sin(i 2 ) 1 sin( r 2 ) 180 ( r i 2 ) 1 h Incoming light p ray 1000nm 2 r 2 i r i 2 2 i 2 1 r i 2 i r Dielectric particle being trapped i 2 Exiting light ray p h ' Scattering force vector Force vector exerted by light on dielectric particle as a result of momentum conservation Electric Dipole Approximation • The force on charge particle in an electric field is given by the Lorentz Force Equation: d 1 1 dE 1 p E 2 2 2 FFE q(E E B) q(E v B) )E F (d ( )E E ) E E ( E) B)B)] p E FF(E q(E [F F ( [(E p E )E ( E) B) B)] 1 2 1 1 tt tt 22 2 t 1 B B E 2 [ E EE( ) B)] 2 t t t 1 2 [ E (E B)] 2 t QuickTime™ and a decompressor are needed to see this picture. Sources Used: • • • A. Ashkin, J.M. Dziedzic, J.E. Bjorkholm and S. Chu. 1986. "Observation of a Single-Beam Gradient Force Optical Trap for Dielectric Particles." Opt. Lett. 11 (5) 288-290. Block S. M. 1992. "Making light work with optical tweezers." Nature 360(6403):493-5. Dholakia, Kishan, Gabriel Spaulding, and Michael Macdonald. "Optical Tweezers: the next Generation." Physics World Oct. 2002. Physicsweb.org. Oct. 2002. Web. 13 Nov. 2010. http://physicsworldarchive.iop.org/index.cfm?action=summary&doc=15%2F1 0%2Fphwv15i10a37%40pwa-xml&qt • Pressurized Viruses, Gelbart, et al.Science 27 March 2009: 16821683.DOI:10.1126/science.1170645 http://www.absoluteastronomy.com/topics/Optical_tweezers